Difference between revisions of "Aufgaben:Exercise 3.6Z: Two Imaginary Poles"
From LNTwww
| (One intermediate revision by the same user not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1786__LZI_Z_3_6.png|right|frame|Two imaginary poles and one zero ]] | + | [[File:P_ID1786__LZI_Z_3_6.png|right|frame|Two imaginary poles <br>and one zero ]] |
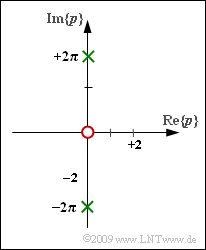
| − | In this exercise, we consider a causal signal $x(t)$ with the Laplace transform | + | In this exercise, we consider a causal signal $x(t)$ with the Laplace transform |
:$$X_{\rm L}(p) = | :$$X_{\rm L}(p) = | ||
\frac { p} { p^2 + 4 \pi^2}= | \frac { p} { p^2 + 4 \pi^2}= | ||
| Line 11: | Line 11: | ||
corresponding to the graph (one red zero and two green poles). | corresponding to the graph (one red zero and two green poles). | ||
| − | In contrast, the signal $y(t)$ has the Laplace spectral function | + | *In contrast, the signal $y(t)$ has the Laplace spectral function |
:$$Y_{\rm L}(p) = | :$$Y_{\rm L}(p) = | ||
\frac { 1} { p^2 + 4 \pi^2} | \frac { 1} { p^2 + 4 \pi^2} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Thus, the red zero does not belong to $Y_{\rm L}(p)$. | + | :Thus, the red zero does not belong to $Y_{\rm L}(p)$. |
| − | Finally, the signal $z(t)$ with the Laplace tansform | + | *Finally, the signal $z(t)$ with the Laplace tansform |
:$$Z_{\rm L}(p) = | :$$Z_{\rm L}(p) = | ||
\frac { p} { (p-{\rm j} \cdot \beta)(p+{\rm j} \cdot \beta)} | \frac { p} { (p-{\rm j} \cdot \beta)(p+{\rm j} \cdot \beta)} | ||
\hspace{0.05cm}$$ | \hspace{0.05cm}$$ | ||
| − | is considered, in particular the limiting case for $\beta → 0$. | + | :is considered, in particular the limiting case for $\beta → 0$. |
| Line 27: | Line 27: | ||
| − | + | Please note: | |
| − | |||
| − | |||
| − | |||
*The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform|Inverse Laplace Transform]]. | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform|Inverse Laplace Transform]]. | ||
| − | *The frequency variable $p$ is normalized such that time $t$ is in microseconds after applying the residue theorem. | + | *The frequency variable $p$ is normalized such that time $t$ is in microseconds after applying the residue theorem. |
*A result $t = 1$ is thus to be interpreted as $t = T$ with $T = 1 \ \rm µ s$ . | *A result $t = 1$ is thus to be interpreted as $t = T$ with $T = 1 \ \rm µ s$ . | ||
*The [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform#Formulation_of_the_residue_theorem|residue theorem]] is as follows using the example of the function $X_{\rm L}(p)$ with two simple poles at $ \pm {\rm j} \cdot \beta$: | *The [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform#Formulation_of_the_residue_theorem|residue theorem]] is as follows using the example of the function $X_{\rm L}(p)$ with two simple poles at $ \pm {\rm j} \cdot \beta$: | ||
| Line 46: | Line 43: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Compute the signal $x(t)$. Which of the following statements are correct? | + | {Compute the signal $x(t)$. Which of the following statements are correct? |
|type="[]"} | |type="[]"} | ||
+ $x(t)$ is a causal cosine signal. | + $x(t)$ is a causal cosine signal. | ||
- $x(t)$ is a causal sinusoidal signal. | - $x(t)$ is a causal sinusoidal signal. | ||
+ The amplitude of $x(t)$ is $1$. | + The amplitude of $x(t)$ is $1$. | ||
| − | + The period of $x(t)$ is $T = 1 \ \rm µ s$. | + | + The period of $x(t)$ is $T = 1 \ \rm µ s$. |
| Line 74: | Line 71: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The <u>suggested solutions 1, 3 and 4</u> are correct: | + | '''(1)''' The <u>suggested solutions 1, 3 and 4</u> are correct: |
*The following is obtained for signal $x(t)$ for positive times by applying the residue theorem: | *The following is obtained for signal $x(t)$ for positive times by applying the residue theorem: | ||
:$$x_1(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} | :$$x_1(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} | ||
| Line 97: | Line 94: | ||
| − | '''(2)''' The <u>suggested solutions 2 and 4</u> are correct: | + | '''(2)''' The <u>suggested solutions 2 and 4</u> are correct: |
| − | *In principle, this subtask could be solved in the same way as subtask '''(1)'''. | + | *In principle, this subtask could be solved in the same way as subtask '''(1)'''. |
| − | *However, the integration theorem can also be used. | + | *However, the integration theorem can also be used. |
*This says among other things that multiplication by $1/p$ in the spectral domain corresponds to integration in the time domain: | *This says among other things that multiplication by $1/p$ in the spectral domain corresponds to integration in the time domain: | ||
:$$Y_{\rm L}(p) = {1}/{p} \cdot X_{\rm L}(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} t \ge 0:\quad y(t) = \int_{-\infty}^t \cos(2\pi | :$$Y_{\rm L}(p) = {1}/{p} \cdot X_{\rm L}(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} t \ge 0:\quad y(t) = \int_{-\infty}^t \cos(2\pi | ||
| Line 105: | Line 102: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | Please note: The causal cosine signal $x(t)$ and the causal sine signal $y(t)$ are shown on the information page of [[Aufgaben:Exercise_3.6:_Transient_Behavior|Exercise 3.6]] as $c_{\rm K}(t)$ and $s_{\rm K}(t)$, respectively. | |
| − | '''(3)''' The <u>suggested solutions 1 and 3</u> are correct: | + | '''(3)''' The <u>suggested solutions 1 and 3</u> are correct: |
| − | *A comparison with the computation of $x(t)$ shows that $z(t) = \cos (\beta \cdot t)$ holds for $t \ge 0$ and $z(t) = 0$ for $t < 0$ | + | *A comparison with the computation of $x(t)$ shows that $z(t) = \cos (\beta \cdot t)$ holds for $t \ge 0$ and $z(t) = 0$ for $t < 0$. |
*The limit process for $\beta → 0$ thus results in the step function $\gamma(t)$. | *The limit process for $\beta → 0$ thus results in the step function $\gamma(t)$. | ||
*The same result is obtained by consideration in the spectral domain: | *The same result is obtained by consideration in the spectral domain: | ||
Latest revision as of 17:33, 9 December 2021
In this exercise, we consider a causal signal $x(t)$ with the Laplace transform
- $$X_{\rm L}(p) = \frac { p} { p^2 + 4 \pi^2}= \frac { p} { (p-{\rm j} \cdot 2\pi)(p+{\rm j} \cdot 2\pi)} \hspace{0.05cm}$$
corresponding to the graph (one red zero and two green poles).
- In contrast, the signal $y(t)$ has the Laplace spectral function
- $$Y_{\rm L}(p) = \frac { 1} { p^2 + 4 \pi^2} \hspace{0.05cm}.$$
- Thus, the red zero does not belong to $Y_{\rm L}(p)$.
- Finally, the signal $z(t)$ with the Laplace tansform
- $$Z_{\rm L}(p) = \frac { p} { (p-{\rm j} \cdot \beta)(p+{\rm j} \cdot \beta)} \hspace{0.05cm}$$
- is considered, in particular the limiting case for $\beta → 0$.
Please note:
- The exercise belongs to the chapter Inverse Laplace Transform.
- The frequency variable $p$ is normalized such that time $t$ is in microseconds after applying the residue theorem.
- A result $t = 1$ is thus to be interpreted as $t = T$ with $T = 1 \ \rm µ s$ .
- The residue theorem is as follows using the example of the function $X_{\rm L}(p)$ with two simple poles at $ \pm {\rm j} \cdot \beta$:
- $$x(t) = X_{\rm L}(p) \cdot (p - {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p\hspace{0.05cm} \cdot \hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm} \cdot\hspace{0.05cm} \it \beta}}+X_{\rm L}(p) \cdot (p + {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm} \cdot\hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{-\rm j \hspace{0.05cm} \cdot\hspace{0.05cm} \it \beta}} \hspace{0.05cm}.$$
Questions
Solution
(1) The suggested solutions 1, 3 and 4 are correct:
- The following is obtained for signal $x(t)$ for positive times by applying the residue theorem:
- $$x_1(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm}t}\}= \frac {p} { p+{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= \frac{1}{2} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}\hspace{0.05cm} ,$$
- $$ x_2(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm} t}\}= \frac {p} { p-{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= -{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= \frac{1}{2} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t} \hspace{0.05cm} .$$
- $$\Rightarrow \hspace{0.3cm} x(t) = x_1(t) + x_2(t) = {1}/{2} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}+{\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}\right ] = \cos(2\pi t) \hspace{0.05cm} .$$
(2) The suggested solutions 2 and 4 are correct:
- In principle, this subtask could be solved in the same way as subtask (1).
- However, the integration theorem can also be used.
- This says among other things that multiplication by $1/p$ in the spectral domain corresponds to integration in the time domain:
- $$Y_{\rm L}(p) = {1}/{p} \cdot X_{\rm L}(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} t \ge 0:\quad y(t) = \int_{-\infty}^t \cos(2\pi \tau)\,\,{\rm d}\tau = {1}/({2\pi}) \cdot \sin(2\pi t) \hspace{0.05cm} .$$
Please note: The causal cosine signal $x(t)$ and the causal sine signal $y(t)$ are shown on the information page of Exercise 3.6 as $c_{\rm K}(t)$ and $s_{\rm K}(t)$, respectively.
(3) The suggested solutions 1 and 3 are correct:
- A comparison with the computation of $x(t)$ shows that $z(t) = \cos (\beta \cdot t)$ holds for $t \ge 0$ and $z(t) = 0$ for $t < 0$.
- The limit process for $\beta → 0$ thus results in the step function $\gamma(t)$.
- The same result is obtained by consideration in the spectral domain:
- $$Z_{\rm L}(p) = \lim_{\beta \hspace{0.05cm} \rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}\frac{p}{p^2 + \beta^2} = {1}/{p} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z(t) = \gamma(t) \hspace{0.05cm} .$$