Difference between revisions of "Aufgaben:Exercise 2.8: Asymmetrical Channel"
m |
m |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Envelope_Demodulation |
}} | }} | ||
[[File:P_ID1038__Mod_A_2_8.png|right|frame|Equivalent low-pass signal <br>in the complex plane]] | [[File:P_ID1038__Mod_A_2_8.png|right|frame|Equivalent low-pass signal <br>in the complex plane]] | ||
| − | A cosine-shaped source signal $q(t)$ with amplitude $A_{\rm N}$ and frequency $f_{\rm N}$ is | + | A cosine-shaped source signal $q(t)$ with amplitude $A_{\rm N}$ and frequency $f_{\rm N}$ is double-sideband amplitude modulated. The modulated signal is given by: |
:$$ s(t) = \big[ q(t) + A_{\rm T}\big] \cdot \cos(2 \pi \cdot f_{\rm T} \cdot t ) \hspace{0.05cm}.$$ | :$$ s(t) = \big[ q(t) + A_{\rm T}\big] \cdot \cos(2 \pi \cdot f_{\rm T} \cdot t ) \hspace{0.05cm}.$$ | ||
The transmission channel exhibits linear distortions: | The transmission channel exhibits linear distortions: | ||
*While the lower sideband $($LSB frequency: $f_{\rm T} - f_{\rm N})$ and the carrier are transmitted undistorted, | *While the lower sideband $($LSB frequency: $f_{\rm T} - f_{\rm N})$ and the carrier are transmitted undistorted, | ||
| − | *the upper sideband $($USB | + | *the upper sideband $($USB frequency: $f_{\rm T} + f_{\rm N})$ is weighted with the attenuation factor $α_{\rm O} = 0.25$. |
| − | The graph shows the locus curve, i.e., the representation of the equivalent low-pass signal $r_{\rm TP}(t)$ in the complex plane. | + | The graph shows the locus curve, i.e., the representation of the equivalent low-pass signal $r_{\rm TP}(t)$ in the complex plane. |
| − | Evaluating the signal $r(t)$ with an ideal envelope demodulator, we obtain a sink signal $v(t)$, which can be approximated as follows: | + | Evaluating the signal $r(t)$ with an ideal envelope demodulator, we obtain a sink signal $v(t)$, which can be approximated as follows: |
:$$v(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t ) -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t )-\text{ ...}$$ | :$$v(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t ) -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t )-\text{ ...}$$ | ||
| − | For this measurement, the message frequency $f_{\rm N} = 2 \ \rm kHz$ was used. | + | For this measurement, the message frequency $f_{\rm N} = 2 \ \rm kHz$ was used. |
In subtask '''(7)''' the signal-to-noise power ratio $\rm (SNR)$ should be calculated as follows: | In subtask '''(7)''' the signal-to-noise power ratio $\rm (SNR)$ should be calculated as follows: | ||
| − | :$$ \rho_{v } = | + | :$$ \rho_{v } = P_{v 1}/P_{\varepsilon } \hspace{0.05cm}.$$ |
| − | Here, $P_{v1} = α^2 · P_q$ and $P_ε$ denote the "powers" of both signals: | + | Here, $P_{v1} = α^2 · P_q$ and $P_ε$ denote the "powers" of both signals: |
:$$ v_1(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t )\hspace{0.05cm},$$ | :$$ v_1(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t )\hspace{0.05cm},$$ | ||
:$$ \varepsilon(t) = v(t) - v_1(t) \approx -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t ) \hspace{0.05cm}.$$ | :$$ \varepsilon(t) = v(t) - v_1(t) \approx -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t ) \hspace{0.05cm}.$$ | ||
| Line 27: | Line 27: | ||
| − | + | Hints: | |
| − | |||
| − | |||
| − | |||
*This exercise belongs to the chapter [[Modulation_Methods/Envelope_Demodulation|Envelope Demodulation]]. | *This exercise belongs to the chapter [[Modulation_Methods/Envelope_Demodulation|Envelope Demodulation]]. | ||
| − | *Particular reference is made to the | + | *Particular reference is made to the section [[Modulation_Methods/Envelope_Demodulation#Description_using_the_equivalent_low-pass_signal|Description using the equivalent low-pass signal]]. |
| Line 41: | Line 38: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Give the low-pass signal $r_{\rm TP}(t)$ in its analytical form. What value results for time $t = 0$? | + | {Give the low-pass signal $r_{\rm TP}(t)$ in its analytical form. What value results for time $t = 0$? |
|type="{}"} | |type="{}"} | ||
$r_{\rm TP}(t=0) \ = \ $ { 15 3% } $\ \rm V$ | $r_{\rm TP}(t=0) \ = \ $ { 15 3% } $\ \rm V$ | ||
| Line 50: | Line 47: | ||
$A_{\rm N} \ = \ $ { 8 3% } $\ \rm V$ | $A_{\rm N} \ = \ $ { 8 3% } $\ \rm V$ | ||
| − | {Let $f_{\rm N} \hspace{0.15cm}\underline{= 2 \ \rm kHz}$. At which time $t_1$ is the starting point '''(1)''' first reached again after $t = 0$ | + | {Let $f_{\rm N} \hspace{0.15cm}\underline{= 2 \ \rm kHz}$. At which time $t_1$ is the starting point '''(1)''' first reached again after $t = 0$? |
|type="{}"} | |type="{}"} | ||
$t_1 \ = \ $ { 0.5 3% } $\ \rm ms$ | $t_1 \ = \ $ { 0.5 3% } $\ \rm ms$ | ||
| − | {At which | + | {At which time $t_2$ is the elliptical point '''(2)''' with value $\rm j · 3\ V$ reached first? |
|type="{}"} | |type="{}"} | ||
$t_2 \ = \ $ { 0.375 3% } $\ \rm ms$ | $t_2 \ = \ $ { 0.375 3% } $\ \rm ms$ | ||
| − | {Calculate the magnitude function (envelope) $a(t)$ and the phase function $ϕ(t)$ for this time point $t_2$. | + | {Calculate the magnitude function (envelope) $a(t)$ and the phase function $ϕ(t)$ for this time point $t_2$. |
|type="{}"} | |type="{}"} | ||
$a(t = t_2) \ = \ $ { 10.44 3% } $\ \rm V$ | $a(t = t_2) \ = \ $ { 10.44 3% } $\ \rm V$ | ||
| Line 78: | Line 75: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' For a cosine-shaped source signal and attenuation of the upper sideband, it holds that: | + | '''(1)''' For a cosine-shaped source signal and attenuation of the upper sideband, it holds that: |
:$$ r_{\rm TP}(t) = A_{\rm T} + \frac{A_{\rm N}}{2} \cdot \alpha_{\rm O} \cdot{\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm N}\cdot t} + \frac{A_{\rm N}}{2} \cdot{\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm N}\cdot t}\hspace{0.05cm}.$$ | :$$ r_{\rm TP}(t) = A_{\rm T} + \frac{A_{\rm N}}{2} \cdot \alpha_{\rm O} \cdot{\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm N}\cdot t} + \frac{A_{\rm N}}{2} \cdot{\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm N}\cdot t}\hspace{0.05cm}.$$ | ||
*At time $t = 0$ all vectors point in the direction of the real axis. | *At time $t = 0$ all vectors point in the direction of the real axis. | ||
| Line 88: | Line 85: | ||
'''(2)''' The carrier amplitude is defined by the center of the ellipse: | '''(2)''' The carrier amplitude is defined by the center of the ellipse: | ||
$A_{\rm T}\hspace{0.15cm}\underline { = 10 \ \rm V}$. | $A_{\rm T}\hspace{0.15cm}\underline { = 10 \ \rm V}$. | ||
| − | *From the equation given in the first subtask, the amplitude $A_{\rm N}$ can thus also be calculated: | + | *From the equation given in the first subtask, the amplitude $A_{\rm N}$ can thus also be calculated: |
:$$ \frac{A_{\rm N}}{2} \cdot ( 1+ \alpha_0) = r_{\rm TP}(t= 0) - A_{\rm T} = 5 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm N} \hspace{0.15cm}\underline {= 8 \,{\rm V}} \hspace{0.05cm}.$$ | :$$ \frac{A_{\rm N}}{2} \cdot ( 1+ \alpha_0) = r_{\rm TP}(t= 0) - A_{\rm T} = 5 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm N} \hspace{0.15cm}\underline {= 8 \,{\rm V}} \hspace{0.05cm}.$$ | ||
*The point marked '''(2)''' can be used as a check: | *The point marked '''(2)''' can be used as a check: | ||
| Line 95: | Line 92: | ||
| − | '''(3)''' The necessary time for one cycle | + | '''(3)''' The necessary time for one cycle $t_1$ is equal to the time period of the source signal: |
:$$t_1= 1/f_{\rm N} \hspace{0.15cm}\underline {=0.5 \ \rm ms}.$$ | :$$t_1= 1/f_{\rm N} \hspace{0.15cm}\underline {=0.5 \ \rm ms}.$$ | ||
| − | '''(4)''' Since the lower sideband is larger than the upper sideband, the peak of the pointer composite moves clockwise around the ellipse. | + | '''(4)''' Since the lower sideband is larger than the upper sideband, the peak of the pointer composite moves clockwise around the ellipse. |
| − | *Point '''(2)''' is first reached at time $t_2 = 3/4 · t_1\hspace{0.15cm}\underline { = 0.375 \ \rm ms}$ | + | *Point '''(2)''' is first reached at time $t_2 = 3/4 · t_1\hspace{0.15cm}\underline { = 0.375 \ \rm ms}$. |
| Line 110: | Line 107: | ||
*The phase function is: | *The phase function is: | ||
:$$\phi(t = t_2) = {\rm arctan} \frac{3 \,{\rm V}}{10 \,{\rm V}} \hspace{0.15cm}\underline {= 16.7^{\circ}}\hspace{0.05cm}.$$ | :$$\phi(t = t_2) = {\rm arctan} \frac{3 \,{\rm V}}{10 \,{\rm V}} \hspace{0.15cm}\underline {= 16.7^{\circ}}\hspace{0.05cm}.$$ | ||
| − | *The maximum phase $ϕ_{\rm max}$ is slightly larger. It occurs (with a positive sign) at time $t_3 < t_2$ when a straight line from the origin is tangent to the ellipse. | + | *The maximum phase $ϕ_{\rm max}$ is slightly larger. |
| + | *It occurs (with a positive sign) at time $t_3 < t_2$ when a straight line from the origin is tangent to the ellipse. | ||
*By setting up the ellipse equation, this point $(x_3$, $y_3)$ can be accurately calculated analytically. | *By setting up the ellipse equation, this point $(x_3$, $y_3)$ can be accurately calculated analytically. | ||
*From this, the following would hold for the maximum phase: | *From this, the following would hold for the maximum phase: | ||
| − | : | + | :$$\phi_{\rm max} = {\rm arctan} \ {y_3}/{x_3} \hspace{0.05cm}.$$ |
| − | '''(6)''' The distortion factors of second and third order can be obtained from the given | + | '''(6)''' The distortion factors of second and third order can be obtained from the equation given for $v(t)$ $($valid for $f_{\rm N} = 2 \ \rm kHz)$: |
:$$ K_2 = \frac{0.148 \,{\rm V}}{2.424 \,{\rm V}} = 0.061, \hspace{0.3cm} K_3 = \frac{0.056 \,{\rm V}}{2.424 \,{\rm V}} = 0.023 \hspace{0.05cm}.$$ | :$$ K_2 = \frac{0.148 \,{\rm V}}{2.424 \,{\rm V}} = 0.061, \hspace{0.3cm} K_3 = \frac{0.056 \,{\rm V}}{2.424 \,{\rm V}} = 0.023 \hspace{0.05cm}.$$ | ||
| − | *Thus for the total distortion factor we get: | + | *Thus, for the total distortion factor we get: |
:$$K = \sqrt{K_2^2 + K_3^2 }\hspace{0.15cm}\underline { \approx 6.6 \%}.$$ | :$$K = \sqrt{K_2^2 + K_3^2 }\hspace{0.15cm}\underline { \approx 6.6 \%}.$$ | ||
| − | '''(7)''' | + | '''(7)''' From the power of the useful signal and the interference signal, we obtain: |
:$$ P_{v 1} = \frac{(2.424 \,{\rm V})^2}{2} = 2.94 \,{\rm V}^2\hspace{0.05cm},\hspace{0.3cm} P_{\varepsilon} = \frac{(-0.148 \,{\rm V})^2}{2} + \frac{(0.056 \,{\rm V})^2}{2}= 0.0125 \,{\rm V}^2\hspace{0.05cm}$$ | :$$ P_{v 1} = \frac{(2.424 \,{\rm V})^2}{2} = 2.94 \,{\rm V}^2\hspace{0.05cm},\hspace{0.3cm} P_{\varepsilon} = \frac{(-0.148 \,{\rm V})^2}{2} + \frac{(0.056 \,{\rm V})^2}{2}= 0.0125 \,{\rm V}^2\hspace{0.05cm}$$ | ||
*This gives the signal-to-noise power ratio $\rm (SNR)$: | *This gives the signal-to-noise power ratio $\rm (SNR)$: | ||
:$$\rho_{v} = \frac{P_{v 1}}{P_{\varepsilon }}= \frac{(2.94 \,{\rm V})^2}{0.0125 \,{\rm V}^2} \hspace{0.15cm}\underline {\approx 230} = \frac{1}{K^2} \hspace{0.05cm}.$$ | :$$\rho_{v} = \frac{P_{v 1}}{P_{\varepsilon }}= \frac{(2.94 \,{\rm V})^2}{0.0125 \,{\rm V}^2} \hspace{0.15cm}\underline {\approx 230} = \frac{1}{K^2} \hspace{0.05cm}.$$ | ||
| − | *If, on the other hand, the amplitude distortion were also assigned to the error signal, we would arrive at a much smaller $\rm SNR$. | + | *If, on the other hand, the amplitude distortion were also assigned to the error signal, we would arrive at a much smaller $\rm SNR$. |
| − | *When $P_q = A_{\rm N}^2/2 = 8 \ \rm V^2$ and $P_{\varepsilon}\hspace{0.02cm}' = \overline{(v(t)-q(t))^2} = {1}/{2}\cdot ( 4 \,{\rm V} - 2.424 \,{\rm V})^2 + P_{\varepsilon}= 1.254 \,{\rm V}^2$ one would get: | + | *When $P_q = A_{\rm N}^2/2 = 8 \ \rm V^2$ and $P_{\varepsilon}\hspace{0.02cm}' = \overline{(v(t)-q(t))^2} = {1}/{2}\cdot ( 4 \,{\rm V} - 2.424 \,{\rm V})^2 + P_{\varepsilon}= 1.254 \,{\rm V}^2$ one would get: |
:$$\rho_{v }\hspace{0.02cm}' = \frac{8 \,{\rm V}^2}{1.254 \,{\rm V}^2} \approx 6.4\hspace{0.05cm}.$$ | :$$\rho_{v }\hspace{0.02cm}' = \frac{8 \,{\rm V}^2}{1.254 \,{\rm V}^2} \approx 6.4\hspace{0.05cm}.$$ | ||
'''(8)''' All calculations are valid regardless of the message frequency $f_{\rm N}$ if the attenuation factor of the upper sideband remains at $α_{\rm O} = 0.25$ . | '''(8)''' All calculations are valid regardless of the message frequency $f_{\rm N}$ if the attenuation factor of the upper sideband remains at $α_{\rm O} = 0.25$ . | ||
| − | *Thus, the same distortion factor $K\hspace{0.15cm}\underline { \approx 6.6 \%}$ is obtained even for $f_{\rm N} = 4 \ \rm kHz$ . | + | *Thus, the same distortion factor $K\hspace{0.15cm}\underline { \approx 6.6 \%}$ is obtained even for $f_{\rm N} = 4 \ \rm kHz$ . |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:30, 31 March 2022
A cosine-shaped source signal $q(t)$ with amplitude $A_{\rm N}$ and frequency $f_{\rm N}$ is double-sideband amplitude modulated. The modulated signal is given by:
- $$ s(t) = \big[ q(t) + A_{\rm T}\big] \cdot \cos(2 \pi \cdot f_{\rm T} \cdot t ) \hspace{0.05cm}.$$
The transmission channel exhibits linear distortions:
- While the lower sideband $($LSB frequency: $f_{\rm T} - f_{\rm N})$ and the carrier are transmitted undistorted,
- the upper sideband $($USB frequency: $f_{\rm T} + f_{\rm N})$ is weighted with the attenuation factor $α_{\rm O} = 0.25$.
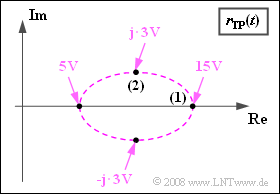
The graph shows the locus curve, i.e., the representation of the equivalent low-pass signal $r_{\rm TP}(t)$ in the complex plane.
Evaluating the signal $r(t)$ with an ideal envelope demodulator, we obtain a sink signal $v(t)$, which can be approximated as follows:
- $$v(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t ) -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t )-\text{ ...}$$
For this measurement, the message frequency $f_{\rm N} = 2 \ \rm kHz$ was used.
In subtask (7) the signal-to-noise power ratio $\rm (SNR)$ should be calculated as follows:
- $$ \rho_{v } = P_{v 1}/P_{\varepsilon } \hspace{0.05cm}.$$
Here, $P_{v1} = α^2 · P_q$ and $P_ε$ denote the "powers" of both signals:
- $$ v_1(t) = 2.424 \,{\rm V} \cdot \cos(\omega_{\rm N} \cdot t )\hspace{0.05cm},$$
- $$ \varepsilon(t) = v(t) - v_1(t) \approx -0.148 \,{\rm V} \cdot \cos(2\omega_{\rm N} \cdot t )+ 0.056 \,{\rm V} \cdot \cos(3\omega_{\rm N} \cdot t ) \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Envelope Demodulation.
- Particular reference is made to the section Description using the equivalent low-pass signal.
Questions
Solution
- $$ r_{\rm TP}(t) = A_{\rm T} + \frac{A_{\rm N}}{2} \cdot \alpha_{\rm O} \cdot{\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm N}\cdot t} + \frac{A_{\rm N}}{2} \cdot{\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm N}\cdot t}\hspace{0.05cm}.$$
- At time $t = 0$ all vectors point in the direction of the real axis.
- Thus $r_{\rm TP}(t = 0)\hspace{0.15cm}\underline { = 15 \ \rm V}$ can be read from the graph on the exercise page.
(2) The carrier amplitude is defined by the center of the ellipse:
$A_{\rm T}\hspace{0.15cm}\underline { = 10 \ \rm V}$.
- From the equation given in the first subtask, the amplitude $A_{\rm N}$ can thus also be calculated:
- $$ \frac{A_{\rm N}}{2} \cdot ( 1+ \alpha_0) = r_{\rm TP}(t= 0) - A_{\rm T} = 5 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm N} \hspace{0.15cm}\underline {= 8 \,{\rm V}} \hspace{0.05cm}.$$
- The point marked (2) can be used as a check:
- $$\frac{A_{\rm N}}{2} \cdot ( 1- \alpha_0) = 3 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm N} = 8 \,{\rm V} \hspace{0.05cm}.$$
(3) The necessary time for one cycle $t_1$ is equal to the time period of the source signal:
- $$t_1= 1/f_{\rm N} \hspace{0.15cm}\underline {=0.5 \ \rm ms}.$$
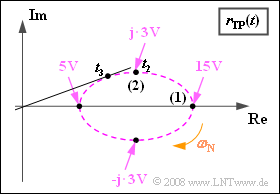
(4) Since the lower sideband is larger than the upper sideband, the peak of the pointer composite moves clockwise around the ellipse.
- Point (2) is first reached at time $t_2 = 3/4 · t_1\hspace{0.15cm}\underline { = 0.375 \ \rm ms}$.
(5) The pointer length at time $t_2$ can be determined with the Pythagorean Theorem :
- $$ a(t = t_2) = \sqrt{(10 \,{\rm V})^2 + (3 \,{\rm V})^2}\hspace{0.15cm}\underline { = 10.44 \,{\rm V}}\hspace{0.05cm}.$$
- The phase function is:
- $$\phi(t = t_2) = {\rm arctan} \frac{3 \,{\rm V}}{10 \,{\rm V}} \hspace{0.15cm}\underline {= 16.7^{\circ}}\hspace{0.05cm}.$$
- The maximum phase $ϕ_{\rm max}$ is slightly larger.
- It occurs (with a positive sign) at time $t_3 < t_2$ when a straight line from the origin is tangent to the ellipse.
- By setting up the ellipse equation, this point $(x_3$, $y_3)$ can be accurately calculated analytically.
- From this, the following would hold for the maximum phase:
- $$\phi_{\rm max} = {\rm arctan} \ {y_3}/{x_3} \hspace{0.05cm}.$$
(6) The distortion factors of second and third order can be obtained from the equation given for $v(t)$ $($valid for $f_{\rm N} = 2 \ \rm kHz)$:
- $$ K_2 = \frac{0.148 \,{\rm V}}{2.424 \,{\rm V}} = 0.061, \hspace{0.3cm} K_3 = \frac{0.056 \,{\rm V}}{2.424 \,{\rm V}} = 0.023 \hspace{0.05cm}.$$
- Thus, for the total distortion factor we get:
- $$K = \sqrt{K_2^2 + K_3^2 }\hspace{0.15cm}\underline { \approx 6.6 \%}.$$
(7) From the power of the useful signal and the interference signal, we obtain:
- $$ P_{v 1} = \frac{(2.424 \,{\rm V})^2}{2} = 2.94 \,{\rm V}^2\hspace{0.05cm},\hspace{0.3cm} P_{\varepsilon} = \frac{(-0.148 \,{\rm V})^2}{2} + \frac{(0.056 \,{\rm V})^2}{2}= 0.0125 \,{\rm V}^2\hspace{0.05cm}$$
- This gives the signal-to-noise power ratio $\rm (SNR)$:
- $$\rho_{v} = \frac{P_{v 1}}{P_{\varepsilon }}= \frac{(2.94 \,{\rm V})^2}{0.0125 \,{\rm V}^2} \hspace{0.15cm}\underline {\approx 230} = \frac{1}{K^2} \hspace{0.05cm}.$$
- If, on the other hand, the amplitude distortion were also assigned to the error signal, we would arrive at a much smaller $\rm SNR$.
- When $P_q = A_{\rm N}^2/2 = 8 \ \rm V^2$ and $P_{\varepsilon}\hspace{0.02cm}' = \overline{(v(t)-q(t))^2} = {1}/{2}\cdot ( 4 \,{\rm V} - 2.424 \,{\rm V})^2 + P_{\varepsilon}= 1.254 \,{\rm V}^2$ one would get:
- $$\rho_{v }\hspace{0.02cm}' = \frac{8 \,{\rm V}^2}{1.254 \,{\rm V}^2} \approx 6.4\hspace{0.05cm}.$$
(8) All calculations are valid regardless of the message frequency $f_{\rm N}$ if the attenuation factor of the upper sideband remains at $α_{\rm O} = 0.25$ .
- Thus, the same distortion factor $K\hspace{0.15cm}\underline { \approx 6.6 \%}$ is obtained even for $f_{\rm N} = 4 \ \rm kHz$ .