Aufgaben:Exercise 3.2: CDF for Exercise 3.1

• Return to book

Given cumulative distribution function  $\rm (CDF)$

The same conditions apply as for  Exercise 3.1.

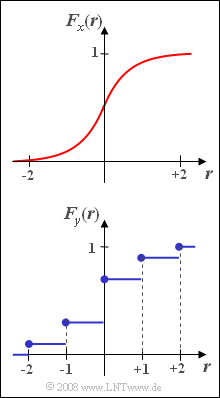
• The PDF of the continuous valued random variable is identically zero in the ranges  $|x| > 2$. 
• In the range  $-2 \le x \le +2$  holds:

$$f_x(x)={1}/{2}\cdot \cos^2({\pi}/{4}\cdot x).$$

• The discrete valued random variable  $y$  is limited too to the range  $\pm 2$  Here,  the following probabilities apply:

$${\rm \Pr}(y=0)=0.4,$$

$${\rm \Pr}(y=+1)={\rm \Pr}(y=-1)=0.2,$$

$${\rm \Pr}(y=+2)={\rm \Pr}(y=-2)=0.1.$$

Hints:

• The exercise belongs to the chapter  Cumulative Distribution Function.
• The topic of this chapter is illustrated with examples in the  (German language)  learning video
      "Zusammenhang zwischen WDF und VTF"   $\Rightarrow$   "Relationship between PDF and CDF".
• Given the following equation:

$$\int \cos^{\rm 2}( ax)\, {\rm d}x=\frac{x}{2}+\frac{1}{4 a}\cdot \sin(2 ax).$$

Questions

1

Which of the following statements are true for the cumulative distribution function  $F_x(r)$  of the continuous valued random variable  $x$ ?

	The CDF is equal for all values  $r \le -2$   ⇒   $F_x(r) \equiv 0$.
	The CDF is equal for all values  $r \ge +2$   ⇒   $F_x(r) \equiv 1$.
	The curve of  $F_x(r)$  is monotonically increasing.

2

Which of the following statements are true for the cumulative distribution function  $F_y(r)$  of the discrete valued random variable  $y$ ?

	The CDF is equal for all values  $r \le -2$   ⇒   $F_y(r) \equiv 0$.
	The CDF is equal for all values  $r \ge +2$   ⇒   $F_y(r) \equiv 1$.
	The curve of  $F_y(r)$  is monotonically increasing.

3

Calculate the CDF  $F_x(r)$.  Restrict yourself to the range  $0 \le r \le +2$.  What value results for  $r = +1$?

$F_x(r=+1) \ = \ $

4

What is the relationship between  $F_x(r)$  and  $F_x(-r)$?  Enter the CDF value  $F_x(r=-1)$.

$F_x(r=-1) \ = \ $

5

Calculate the probability that  $|\hspace{0.05cm}x\hspace{0.05cm}|$  is smaller than  $1$.  Compare the result with the result of subtask  (7)  of Exercise 3.1.

${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}| < 1) \ = \ $

6

What value is obtained for the CDF of the discrete valued random variable  $y$  at the location  $r = 0$?

$F_y(r = 0)\ = \ $

Solution

Solution

(1)  Since the continuous valued random variable  $x$  is limited to the range  $|\hspace{0.05cm}x\hspace{0.05cm}< 2|$,  all three given statements  are correct.

(2)  Only  statements 2 and 3  are correct here:

• For a discrete valued random variable,  the cumulative distribution function increases only weakly monotonically.
• That means:  Except for unit steps,  there are only horizontal sections of the CDF.
• Since at the unit step points the right-hand side limit value   ⇒   $F_y(-2) = 0.1$,  i.e. not equal to zero.

(3)  The CDF  $F_x(r)$  is calculated as the integral from  $-\infty$  to  $r$  over the PDF  $f_x(x)$.

• Due to symmetry,  herefore can be written in the range  $0 \le r \le +2$:

$$F_{x} (r) =\frac{1}{2} + \int_{0}^{r} f_x(x)\;{\rm d}x = \frac{1}{2} + \int_{0}^{ r} {1}/{2}\cdot \cos^2 ({\pi}/{4}\cdot x)\;{\rm d}x.$$

• In the same way as for the subtask  (7)  of Exercise 3.1,  we thus obtain:

$$F_{x} (r) =\frac{1}{2} + \frac{ r}{ 4} + \frac{1}{2 \pi} \cdot \sin({\pi}/{2}\cdot r),$$

$$F_{x} (r=0) =\rm \frac{1}{2} + \rm \frac{1}{2 \pi} \cdot\rm sin(\rm 0)\hspace{0.15cm}{= 0.500},$$

$$F_{x} (r=1) =\rm \frac{1}{2} + \frac{\rm 1}{\rm 4} + \rm \frac{1}{2 \pi}\cdot \rm sin({\pi}/{2})\hspace{0.15cm}\underline{=0.909},$$

$$F_{x} (r=2) =\rm \frac{1}{2} + \frac{\rm1}{\rm 2} + \rm \frac{1}{2 \pi} \cdot \rm sin(\pi)\hspace{0.15cm}{= 1.000}.$$

(4)  Because of the point symmetry around  $r=0$   resp.  $F_{x} (0) = 1/2$  and because of  $\sin(-x) = -\sin(x)$  this formula holds in the whole domain,  as the following control calculation shows:

$$F_{x} (r=-2) =\rm \frac{1}{2} - \frac{\rm1}{\rm 2} - \rm \frac{1}{2 \pi} \cdot\rm sin(\pi)=0,$$

$$F_{x} (r=-1) =\rm \frac{1}{2} - \frac{\rm1}{\rm 4} - \rm \frac{1}{2 \pi} \cdot\rm sin({\pi}/{2})\hspace{0.15cm}\underline{= 0.091}.$$

(5)  For the probability that  $x$  lies between  $-1$  and  $+1$:

$${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}|< 1)= F_{x}(+1) - F_{ x}(-1)= 0.909-0.091\hspace{0.15cm}\underline{= 0.818}.$$

• This result agrees exactly with the result of the subtask  (7)  of Exercise 3.1  which was obtained by direct integration üover the WDF.

(6)  The CDF of the discrete valued random variable  $y$  at the location  $y =0$  is the sum of the probabilities of  $-2$,  $-1$  and  $0$.  So:

$$F_y(r = 0)\hspace{0.15cm}\underline{= 0.7}.$$