Difference between revisions of "Aufgaben:Exercise 5.9: Minimization of the MSE"
| (2 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
[[File:P_ID652__Sto_A_5_9.png|right|frame|Power-spectral densities <br>with the Wiener filter ]] | [[File:P_ID652__Sto_A_5_9.png|right|frame|Power-spectral densities <br>with the Wiener filter ]] | ||
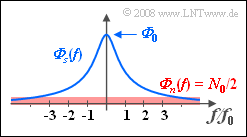
| − | Given a stochastic | + | Given a stochastic signal $s(t)$ of which only the power-spectral density $\rm (PSD)$ is known: |
:$${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$ | :$${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$ | ||
This power-spectral density ${\it \Phi} _s (f)$ is shown in blue in the accompanying diagram. | This power-spectral density ${\it \Phi} _s (f)$ is shown in blue in the accompanying diagram. | ||
| Line 10: | Line 10: | ||
*The average power of $s(t)$ is obtained by integration over the power-spectral density: | *The average power of $s(t)$ is obtained by integration over the power-spectral density: | ||
:$$P_s = \int_{ - \infty }^{ + \infty } {{\it \Phi} _s (f)}\, {\rm d} f = {\it \Phi} _0 \cdot f_0 \cdot {\rm{\pi }}.$$ | :$$P_s = \int_{ - \infty }^{ + \infty } {{\it \Phi} _s (f)}\, {\rm d} f = {\it \Phi} _0 \cdot f_0 \cdot {\rm{\pi }}.$$ | ||
| − | *Additively superimposed on | + | *Additively superimposed on this signal $s(t)$ is white noise $n(t)$ with noise power density ${\it \Phi}_n(f) = N_0/2.$ |
| − | *As an abbreviation, we use $Q = 2 \cdot {\it \Phi}_0/N_0$, where $Q$ could be interpreted as "quality". | + | *As an abbreviation, we use $Q = 2 \cdot {\it \Phi}_0/N_0$, where $Q$ could be interpreted as "quality". |
*Note that $Q$ does not represent a signal–to–noise power ratio. | *Note that $Q$ does not represent a signal–to–noise power ratio. | ||
| − | In this exercise, we want to determine the frequency response $H(f)$ of a filter that minimizes the mean square error $\rm (MSE)$ between the useful signal $s(t)$ and the filter output signal $d(t)$: | + | In this exercise, we want to determine the frequency response $H(f)$ of a filter that minimizes the mean square error $\rm (MSE)$ between the useful signal $s(t)$ and the filter output signal $d(t)$: |
:$${\rm{MSE}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{T_{\rm M} }\int_{ - T_{\rm M} /2}^{T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t.}$$ | :$${\rm{MSE}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{T_{\rm M} }\int_{ - T_{\rm M} /2}^{T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t.}$$ | ||
| Line 21: | Line 21: | ||
| − | + | Notes: | |
| − | |||
| − | |||
| − | |||
*The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Wiener–Kolmogorow–Filter|Wiener–Kolmogorow Filter]]. | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Wiener–Kolmogorow–Filter|Wiener–Kolmogorow Filter]]. | ||
| − | + | *For the optimal frequency response, according to Wiener and Kolmogorov, the following applies in general: | |
| + | :$$H_{\rm WF} (f) = \frac{1}{{1 + {\it \Phi} _n (f)/{\it \Phi} _s (f)}}.$$ | ||
*The following indefinite integral is given for solving: | *The following indefinite integral is given for solving: | ||
:$$\int {\frac{1}{a^2 + x^2 }} \, {\rm{d}}x ={1}/{a} \cdot \arctan \left( {{x}/{a}} \right).$$ | :$$\int {\frac{1}{a^2 + x^2 }} \, {\rm{d}}x ={1}/{a} \cdot \arctan \left( {{x}/{a}} \right).$$ | ||
| Line 38: | Line 36: | ||
{Which of the following statements are true? | {Which of the following statements are true? | ||
|type="[]"} | |type="[]"} | ||
| − | - $H(f)$ is a Gaussian low pass. | + | - $H(f)$ is a Gaussian low-pass. |
- $H(f)$ represents a matched filter. | - $H(f)$ represents a matched filter. | ||
+ $H(f)$ represents a Wiener–Kolmogorov filter. | + $H(f)$ represents a Wiener–Kolmogorov filter. | ||
| − | {Determine the frequency response $H(f)$ of the optimum filter for this purpose. What values result with $Q = 3$ at $f = 0$ and $f = 2f_0$? | + | {Determine the frequency response $H(f)=H_{\rm WF} (f)$ of the optimum filter for this purpose. <br>What values result with $Q = 3$ at $f = 0$ and $f = 2f_0$? |
|type="{}"} | |type="{}"} | ||
$H(f = 0) \ = \ $ { 0.75 3% } | $H(f = 0) \ = \ $ { 0.75 3% } | ||
| Line 49: | Line 47: | ||
| − | {Let $Q = 3$. Calculate the mean square error $(\rm MSE)$ with respect to $P_s$ | + | {Let $Q = 3$. Calculate the mean square error $(\rm MSE)$ with respect to $P_s$ of the best possible filter. |
|type="{}"} | |type="{}"} | ||
${\rm MSE}/P_s \ = \ $ { 0.5 3% } | ${\rm MSE}/P_s \ = \ $ { 0.5 3% } | ||
| − | {How | + | {How must the "quality factor" $Q$ be chosen at least, so that for the quotient the value ${\rm MSE}/P_s = 0.1$ can be reached? |
|type="{}"} | |type="{}"} | ||
$Q_\text{min} \ = \ $ { 99 3% } | $Q_\text{min} \ = \ $ { 99 3% } | ||
| Line 70: | Line 68: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u>Only the last solution</u> is correct: | + | '''(1)''' <u>Only the last solution</u> is correct: |
| − | *The task | + | *The task "Minimization of the mean square error" already points to the Wiener–Kolmogorow filter. |
| − | *The matched filter, on the other hand, is used to concentrate the signal energy and thereby maximize the S/N ratio for a given time. | + | *The matched filter, on the other hand, is used to concentrate the signal energy and thereby maximize the S/N ratio for a given time. |
| − | '''(2)''' For the optimal frequency response, according to Wiener and Kolmogorov, the following applies in general: | + | '''(2)''' For the optimal frequency response, according to Wiener and Kolmogorov, the following applies in general: |
:$$H(f) = H_{\rm WF} (f) = \frac{1}{{1 + {\it \Phi} _n (f)/{\it \Phi} _s (f)}}.$$ | :$$H(f) = H_{\rm WF} (f) = \frac{1}{{1 + {\it \Phi} _n (f)/{\it \Phi} _s (f)}}.$$ | ||
| − | *With the given power-spectral density, it is also possible to write for this: | + | *With the given power-spectral density, it is also possible to write for this: |
:$$H(f) = \frac{1}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} = \frac{1}{{1 + {1}/{Q}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}}.$$ | :$$H(f) = \frac{1}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} = \frac{1}{{1 + {1}/{Q}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}}.$$ | ||
| Line 88: | Line 86: | ||
| − | '''(3)''' For the filter calculated in subtask '''(2)''', taking symmetry into account, the following holds: | + | '''(3)''' For the filter calculated in subtask '''(2)''', taking symmetry into account, the following holds: |
:$${\rm{MSE = }}\int_{-\infty}^{+\infty} H(f) \cdot {\it \Phi} _n (f) \,\, {\rm{d}}f = \int_{0}^{+\infty} \frac{N_0}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} \,\, {\rm{d}}f .$$ | :$${\rm{MSE = }}\int_{-\infty}^{+\infty} H(f) \cdot {\it \Phi} _n (f) \,\, {\rm{d}}f = \int_{0}^{+\infty} \frac{N_0}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} \,\, {\rm{d}}f .$$ | ||
| − | *For this, with $Q = 2 \cdot {\it \Phi}_0/N_0$ and $a^2 = Q + 1$, we can also write:<br /> | + | *For this, with $Q = 2 \cdot {\it \Phi}_0/N_0$ and $a^2 = Q + 1$, we can also write:<br /> |
:$${\rm{MSE = }}\int_0^\infty {\frac{{2{\it \Phi} _0 }}{{ Q+1 + ( {f/f_0 })^2 }}} \,\, {\rm{d}}f = 2{\it \Phi} _0 \cdot f_0 \int_0^\infty {\frac{1}{a^2 + x^2 }}\,\, {\rm{d}}x.$$ | :$${\rm{MSE = }}\int_0^\infty {\frac{{2{\it \Phi} _0 }}{{ Q+1 + ( {f/f_0 })^2 }}} \,\, {\rm{d}}f = 2{\it \Phi} _0 \cdot f_0 \int_0^\infty {\frac{1}{a^2 + x^2 }}\,\, {\rm{d}}x.$$ | ||
| − | * | + | *This leads to the result with the integral given: |
:$${\rm{MSE}} = \frac{{2{\it \Phi} _0 f_0 }}{{\sqrt {1 + Q} }}\left( {\arctan ( \infty ) - \arctan ( 0 )} \right) = \frac{{{\it \Phi} _0 f_0 {\rm{\pi }}}}{{\sqrt {1 + Q} }}.$$ | :$${\rm{MSE}} = \frac{{2{\it \Phi} _0 f_0 }}{{\sqrt {1 + Q} }}\left( {\arctan ( \infty ) - \arctan ( 0 )} \right) = \frac{{{\it \Phi} _0 f_0 {\rm{\pi }}}}{{\sqrt {1 + Q} }}.$$ | ||
| − | *Normalizing MSE to the | + | *Normalizing MSE to the power $P_s$ of the signal $s(t)$, we obtain for $Q=3$: |
:$$\frac{\rm{MSE}}{P_s} = \frac{1}{{\sqrt {1 + Q} }} \hspace{0.15cm}\underline { = 0.5}.$$ | :$$\frac{\rm{MSE}}{P_s} = \frac{1}{{\sqrt {1 + Q} }} \hspace{0.15cm}\underline { = 0.5}.$$ | ||
| Line 103: | Line 101: | ||
'''(4)''' From the calculation in subtask '''(3)''', the condition $Q \ge 99$ ⇒ $Q_{\rm min} \hspace{0.15cm}\underline{= 99}$ follows directly for ${\rm MSE}/P_s \ge 0.1.$ | '''(4)''' From the calculation in subtask '''(3)''', the condition $Q \ge 99$ ⇒ $Q_{\rm min} \hspace{0.15cm}\underline{= 99}$ follows directly for ${\rm MSE}/P_s \ge 0.1.$ | ||
| − | *The larger $Q$ | + | *The larger $Q$, the smaller the mean square error becomes. |
| − | '''(5)''' <u>Only the second solution</u> is correct: | + | '''(5)''' <u>Only the second solution</u> is correct: |
*A frequency response of the same shape as the Wiener–Kolmogorov filter ⇒ $H(f) = K \cdot H_{\rm WF}(f)$ with $K \ne 1$ always leads to large distortions. | *A frequency response of the same shape as the Wiener–Kolmogorov filter ⇒ $H(f) = K \cdot H_{\rm WF}(f)$ with $K \ne 1$ always leads to large distortions. | ||
| − | *This can be illustrated | + | *This can be illustrated by the noise-free case $(Q \to \infty)$: $d(t) = K \cdot s(t)$ and the optimization task would be extremely poorly solved despite good conditions. |
| − | * | + | *One might incorrectly conclude from the equation |
| + | [[File:P_ID651__Sto_A_5_9_e.png|right|frame|Power-spectral density with the <br>Wiener–Kolmogorov filter]] | ||
| + | |||
:$${\rm{MSE}} = \int_{ - \infty }^{ + \infty } {H_{\rm WF} (f)} \cdot \it{\Phi} _n (f)\,\,{\rm{d}}f$$ | :$${\rm{MSE}} = \int_{ - \infty }^{ + \infty } {H_{\rm WF} (f)} \cdot \it{\Phi} _n (f)\,\,{\rm{d}}f$$ | ||
| − | : | + | :that a filter $H(f) = 2 \cdot H_{\rm WF}(f)$ only doubles the mean squared error. |
| − | *However, this is not the case, since $H(f)$ is then no longer a Wiener filter and the above equation is | + | *However, this is not the case, since $H(f)$ is then no longer a Wiener filter and the above equation is no longer applicable. |
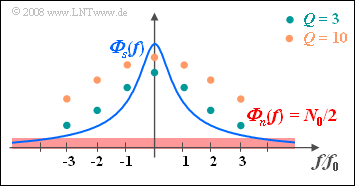
| − | + | The second statement is true, as can be seen from the accompanying diagram. | |
| − | The second statement is true, as can be seen from the accompanying diagram. | + | *The dots mark the frequency response $H_{\rm WF}(f)$ of the filter for $Q = 3$ and for $Q = 10$, resp. |
| − | *The dots mark the frequency response $H_{\rm WF}(f | ||
*For larger $Q (= 10)$, high components are attenuated less than for lower $Q (= 3)$. | *For larger $Q (= 10)$, high components are attenuated less than for lower $Q (= 3)$. | ||
| − | *Therefore, in the case of $Q = 10$, the filter output signal | + | *Therefore, in the case of $Q = 10$, the filter output signal contains more higher frequency components, which are due to the noise $n(t)$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 15:35, 23 February 2022
Given a stochastic signal $s(t)$ of which only the power-spectral density $\rm (PSD)$ is known:
- $${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$
This power-spectral density ${\it \Phi} _s (f)$ is shown in blue in the accompanying diagram.
- The average power of $s(t)$ is obtained by integration over the power-spectral density:
- $$P_s = \int_{ - \infty }^{ + \infty } {{\it \Phi} _s (f)}\, {\rm d} f = {\it \Phi} _0 \cdot f_0 \cdot {\rm{\pi }}.$$
- Additively superimposed on this signal $s(t)$ is white noise $n(t)$ with noise power density ${\it \Phi}_n(f) = N_0/2.$
- As an abbreviation, we use $Q = 2 \cdot {\it \Phi}_0/N_0$, where $Q$ could be interpreted as "quality".
- Note that $Q$ does not represent a signal–to–noise power ratio.
In this exercise, we want to determine the frequency response $H(f)$ of a filter that minimizes the mean square error $\rm (MSE)$ between the useful signal $s(t)$ and the filter output signal $d(t)$:
- $${\rm{MSE}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{T_{\rm M} }\int_{ - T_{\rm M} /2}^{T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t.}$$
Notes:
- The exercise belongs to the chapter Wiener–Kolmogorow Filter.
- For the optimal frequency response, according to Wiener and Kolmogorov, the following applies in general:
- $$H_{\rm WF} (f) = \frac{1}{{1 + {\it \Phi} _n (f)/{\it \Phi} _s (f)}}.$$
- The following indefinite integral is given for solving:
- $$\int {\frac{1}{a^2 + x^2 }} \, {\rm{d}}x ={1}/{a} \cdot \arctan \left( {{x}/{a}} \right).$$
Questions
Solution
- The task "Minimization of the mean square error" already points to the Wiener–Kolmogorow filter.
- The matched filter, on the other hand, is used to concentrate the signal energy and thereby maximize the S/N ratio for a given time.
(2) For the optimal frequency response, according to Wiener and Kolmogorov, the following applies in general:
- $$H(f) = H_{\rm WF} (f) = \frac{1}{{1 + {\it \Phi} _n (f)/{\it \Phi} _s (f)}}.$$
- With the given power-spectral density, it is also possible to write for this:
- $$H(f) = \frac{1}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} = \frac{1}{{1 + {1}/{Q}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}}.$$
- With $Q = 3$ it follows:
- $$H( {f = 0} ) = \frac{1}{{1 + {1}/{Q}}} = \frac{Q}{Q + 1} \hspace{0.15cm}\underline {= 0.75},$$
- $$H( {f = 2f_0 } ) = \frac{1}{{1 + {5}/{Q}}} = \frac{Q}{Q + 5} \hspace{0.15cm}\underline {= 0.375}.$$
(3) For the filter calculated in subtask (2), taking symmetry into account, the following holds:
- $${\rm{MSE = }}\int_{-\infty}^{+\infty} H(f) \cdot {\it \Phi} _n (f) \,\, {\rm{d}}f = \int_{0}^{+\infty} \frac{N_0}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} \,\, {\rm{d}}f .$$
- For this, with $Q = 2 \cdot {\it \Phi}_0/N_0$ and $a^2 = Q + 1$, we can also write:
- $${\rm{MSE = }}\int_0^\infty {\frac{{2{\it \Phi} _0 }}{{ Q+1 + ( {f/f_0 })^2 }}} \,\, {\rm{d}}f = 2{\it \Phi} _0 \cdot f_0 \int_0^\infty {\frac{1}{a^2 + x^2 }}\,\, {\rm{d}}x.$$
- This leads to the result with the integral given:
- $${\rm{MSE}} = \frac{{2{\it \Phi} _0 f_0 }}{{\sqrt {1 + Q} }}\left( {\arctan ( \infty ) - \arctan ( 0 )} \right) = \frac{{{\it \Phi} _0 f_0 {\rm{\pi }}}}{{\sqrt {1 + Q} }}.$$
- Normalizing MSE to the power $P_s$ of the signal $s(t)$, we obtain for $Q=3$:
- $$\frac{\rm{MSE}}{P_s} = \frac{1}{{\sqrt {1 + Q} }} \hspace{0.15cm}\underline { = 0.5}.$$
(4) From the calculation in subtask (3), the condition $Q \ge 99$ ⇒ $Q_{\rm min} \hspace{0.15cm}\underline{= 99}$ follows directly for ${\rm MSE}/P_s \ge 0.1.$
- The larger $Q$, the smaller the mean square error becomes.
(5) Only the second solution is correct:
- A frequency response of the same shape as the Wiener–Kolmogorov filter ⇒ $H(f) = K \cdot H_{\rm WF}(f)$ with $K \ne 1$ always leads to large distortions.
- This can be illustrated by the noise-free case $(Q \to \infty)$: $d(t) = K \cdot s(t)$ and the optimization task would be extremely poorly solved despite good conditions.
- One might incorrectly conclude from the equation
- $${\rm{MSE}} = \int_{ - \infty }^{ + \infty } {H_{\rm WF} (f)} \cdot \it{\Phi} _n (f)\,\,{\rm{d}}f$$
- that a filter $H(f) = 2 \cdot H_{\rm WF}(f)$ only doubles the mean squared error.
- However, this is not the case, since $H(f)$ is then no longer a Wiener filter and the above equation is no longer applicable.
The second statement is true, as can be seen from the accompanying diagram.
- The dots mark the frequency response $H_{\rm WF}(f)$ of the filter for $Q = 3$ and for $Q = 10$, resp.
- For larger $Q (= 10)$, high components are attenuated less than for lower $Q (= 3)$.
- Therefore, in the case of $Q = 10$, the filter output signal contains more higher frequency components, which are due to the noise $n(t)$.