Difference between revisions of "Aufgaben:Exercise 1.2: Bit Error Rate"
| (2 intermediate revisions by one other user not shown) | |||
| Line 4: | Line 4: | ||
| − | [[File:P_ID1264__Dig_A_1_2.png|right|frame|Table of Gaussian error functions]] | + | [[File:P_ID1264__Dig_A_1_2.png|right|frame|Table of two Gaussian error functions]] |
It is known from a digital transmission system that it can be approximated by a | It is known from a digital transmission system that it can be approximated by a | ||
| − | BSC model ( | + | BSC model ("Binary Symmetrical Channel") with error probability $p$. |
| − | For verification, the bit error rate is to be determined by comparing the sink symbol sequence $ \langle v_\nu \rangle $ with the source symbol sequence | + | For verification, the bit error rate is to be determined by comparing the sink symbol sequence $ \langle v_\nu \rangle $ with the source symbol sequence |
$ \langle q_\nu \rangle $ and finding the error sequence $ \langle e_\nu \rangle $. Thereby holds: | $ \langle q_\nu \rangle $ and finding the error sequence $ \langle e_\nu \rangle $. Thereby holds: | ||
| − | $$e_\nu = \left\{ \begin{array}{c} 0 \\ | + | :$$e_\nu = \left\{ \begin{array}{c} 0 \\ |
1 \\ \end{array} \right.\quad | 1 \\ \end{array} \right.\quad | ||
\begin{array}{*{1}c} {\rm{for}} | \begin{array}{*{1}c} {\rm{for}} | ||
| Line 18: | Line 18: | ||
v_\nu \ne q_\nu . \\ | v_\nu \ne q_\nu . \\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | The bit error rate is an approximation for the bit error probability $p$ | + | The bit error rate is an approximation for the bit error probability $p$: |
:$${\rm BER} = \frac{1}{N}\cdot\sum_{\nu=1}^N e_\nu.$$ | :$${\rm BER} = \frac{1}{N}\cdot\sum_{\nu=1}^N e_\nu.$$ | ||
| − | The larger the simulation parameter $N$ is chosen, the more accurate this approximation | + | The larger the simulation parameter $N$ is chosen, the more accurate is this approximation. |
| − | From [[Aufgaben:Exercise_3.7:_Bit_Error_Rate_(BER)|Exercise 3.7]] in the book "Stochastic Signal Theory" it is known that the random variable "BER" is actually binomially distributed, but can be approximated with good approximation by a (discrete) Gaussian distribution with mean $p$ and standard deviation $\sigma$: | + | From [[Aufgaben:Exercise_3.7:_Bit_Error_Rate_(BER)|"Exercise 3.7"]] in the book "Stochastic Signal Theory" it is known that the random variable "BER" is actually binomially distributed, but can be approximated with good approximation by a (discrete) Gaussian distribution with mean $p$ and standard deviation $\sigma$: |
:$$\sigma = \sqrt{\frac{ p\cdot (\rm 1- \it p)}{N}}.$$ | :$$\sigma = \sqrt{\frac{ p\cdot (\rm 1- \it p)}{N}}.$$ | ||
| Line 29: | Line 29: | ||
| − | + | Notes: | |
| − | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission|Error Probability for Baseband Transmission]]. | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission|"Error Probability for Baseband Transmission"]]. |
| − | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|Gaussian Distributed Random Variables]] in the book "Stochastic Signal Theory". | + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|"Gaussian Distributed Random Variables"]] in the book "Stochastic Signal Theory". |
| − | *In the table some values of the Gaussian error functions $\rm \phi(x)$ and $\rm Q(x)$ are given. | + | *In the table some values of the Gaussian error functions ${\rm \phi}(x)$ and ${\rm Q}(x)$ are given. |
| Line 43: | Line 43: | ||
- $\rm BER$ is a probability. | - $\rm BER$ is a probability. | ||
+ $\rm BER$ is a relative frequency. | + $\rm BER$ is a relative frequency. | ||
| − | - If $N$ is sufficiently large, $\rm BER$ coincides <b>exactly</b> with $p$ | + | - If $N$ is sufficiently large, $\rm BER$ coincides <b>exactly</b> with $p$. |
| Line 67: | Line 67: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u>Only the second statement</u> is correct: | + | '''(1)''' <u>Only the second statement</u> is correct: |
| − | *$\rm BER$ is the quotient of the number $n_{\rm B}$ of detected symbol errors and the number $N$ of all simulated symbols and thus actually a relative frequency. | + | *$\rm BER$ is the quotient of the number $n_{\rm B}$ of detected symbol errors and the number $N$ of all simulated symbols and thus actually a relative frequency. |
| − | *The probability that ${\rm BER} = p$ is always exactly zero, since $\rm BER$ is a continuous random variable. | + | *The probability that ${\rm BER} = p$ is always exactly zero, since $\rm BER$ is a continuous random variable. |
| − | *However, the probability that $\rm BER$ lies in a narrow interval around $p$ increases as $N$ increases. | + | *However, the probability that $\rm BER$ lies in a narrow interval around $p$ increases as $N$ increases. |
| − | '''(2)''' The standard deviation of the Gaussian random variable $\rm BER$ with $N = 10^6$ and $p = 10^{-2}$ is given by | + | '''(2)''' The standard deviation of the Gaussian random variable $\rm BER$ with $N = 10^6$ and $p = 10^{-2}$ is given by |
:$$\sigma = \sqrt{{ p\cdot (\rm 1- \it p)}/{N}}\approx \sqrt{{ p}/{N}}\hspace{0.1cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$ | :$$\sigma = \sqrt{{ p\cdot (\rm 1- \it p)}/{N}}\approx \sqrt{{ p}/{N}}\hspace{0.1cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' The probability that the $\rm BER$ takes a value outside the range | + | '''(3)''' The probability that the $\rm BER$ takes a value outside the range |
| − | $0.95 \cdot p$ ... $1.05 \cdot p$ is obtained with $\varepsilon = 5 \cdot | + | $0.95 \cdot p$ ... $1.05 \cdot p$ is obtained with $\varepsilon = 5 \cdot 10^{-4}$ $(p = 10^{-2})$ as follows. |
:$${\rm Pr} \left( {\rm BER} < 0.95 \cdot 10^{-2} \right) | :$${\rm Pr} \left( {\rm BER} < 0.95 \cdot 10^{-2} \right) | ||
= {\rm Pr} \left( {\rm BER} > 1.05 \cdot 10^{-2} \right) | = {\rm Pr} \left( {\rm BER} > 1.05 \cdot 10^{-2} \right) | ||
| Line 87: | Line 87: | ||
| − | '''(4)''' With $p = 10^{-4}$, the comparable probability is: | + | '''(4)''' With $p = 10^{-4}$, the comparable probability is: |
:$${\rm Pr} \left( |{\rm BER} - 10^{-4}| > 0.05 \cdot 10^{-4} \right) | :$${\rm Pr} \left( |{\rm BER} - 10^{-4}| > 0.05 \cdot 10^{-4} \right) | ||
= 2 \cdot {\rm Q} \left( {\varepsilon}/{\sigma} | = 2 \cdot {\rm Q} \left( {\varepsilon}/{\sigma} | ||
| Line 98: | Line 98: | ||
| − | '''(5)''' This condition can be formulated with $\varepsilon = 5 \cdot 10^{-6}$ as follows: | + | '''(5)''' This condition can be formulated with $\varepsilon = 5 \cdot 10^{-6}$ as follows: |
:$${\rm Q} \left( {\varepsilon}/{\sigma} \right) < 0.1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$${\rm Q} \left( {\varepsilon}/{\sigma} \right) < 0.1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
{\varepsilon}/{\sigma} > {\rm Q}^{-1}(0.05) \approx 1.64 | {\varepsilon}/{\sigma} > {\rm Q}^{-1}(0.05) \approx 1.64 | ||
Latest revision as of 15:51, 9 May 2022
It is known from a digital transmission system that it can be approximated by a BSC model ("Binary Symmetrical Channel") with error probability $p$.
For verification, the bit error rate is to be determined by comparing the sink symbol sequence $ \langle v_\nu \rangle $ with the source symbol sequence $ \langle q_\nu \rangle $ and finding the error sequence $ \langle e_\nu \rangle $. Thereby holds:
- $$e_\nu = \left\{ \begin{array}{c} 0 \\ 1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} v_\nu = q_\nu \hspace{0.05cm}, \\ v_\nu \ne q_\nu . \\ \end{array}$$
The bit error rate is an approximation for the bit error probability $p$:
- $${\rm BER} = \frac{1}{N}\cdot\sum_{\nu=1}^N e_\nu.$$
The larger the simulation parameter $N$ is chosen, the more accurate is this approximation.
From "Exercise 3.7" in the book "Stochastic Signal Theory" it is known that the random variable "BER" is actually binomially distributed, but can be approximated with good approximation by a (discrete) Gaussian distribution with mean $p$ and standard deviation $\sigma$:
- $$\sigma = \sqrt{\frac{ p\cdot (\rm 1- \it p)}{N}}.$$
Notes:
- The exercise belongs to the chapter "Error Probability for Baseband Transmission".
- Reference is also made to the chapter "Gaussian Distributed Random Variables" in the book "Stochastic Signal Theory".
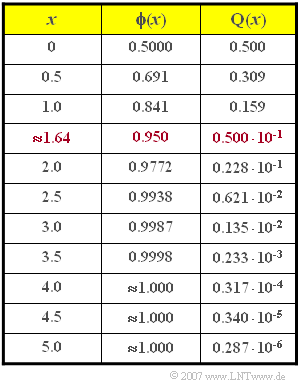
- In the table some values of the Gaussian error functions ${\rm \phi}(x)$ and ${\rm Q}(x)$ are given.
Questions
Solution
- $\rm BER$ is the quotient of the number $n_{\rm B}$ of detected symbol errors and the number $N$ of all simulated symbols and thus actually a relative frequency.
- The probability that ${\rm BER} = p$ is always exactly zero, since $\rm BER$ is a continuous random variable.
- However, the probability that $\rm BER$ lies in a narrow interval around $p$ increases as $N$ increases.
(2) The standard deviation of the Gaussian random variable $\rm BER$ with $N = 10^6$ and $p = 10^{-2}$ is given by
- $$\sigma = \sqrt{{ p\cdot (\rm 1- \it p)}/{N}}\approx \sqrt{{ p}/{N}}\hspace{0.1cm}\underline {= 10^{-4}}\hspace{0.05cm}.$$
(3) The probability that the $\rm BER$ takes a value outside the range
$0.95 \cdot p$ ... $1.05 \cdot p$ is obtained with $\varepsilon = 5 \cdot 10^{-4}$ $(p = 10^{-2})$ as follows.
- $${\rm Pr} \left( {\rm BER} < 0.95 \cdot 10^{-2} \right) = {\rm Pr} \left( {\rm BER} > 1.05 \cdot 10^{-2} \right) = {\rm Q} \left({\varepsilon}/{\sigma} \right)$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr} \left( |{\rm BER} - p| > \varepsilon \right) = 2 \cdot {\rm Q} \left( \frac{5 \cdot 10^{-4}}{10^{-4}} \right) = 2 \cdot 0.287 \cdot 10^{-6}\hspace{0.1cm}\underline {= 0.00574 \cdot 10^{-4}}\hspace{0.05cm}.$$
(4) With $p = 10^{-4}$, the comparable probability is:
- $${\rm Pr} \left( |{\rm BER} - 10^{-4}| > 0.05 \cdot 10^{-4} \right) = 2 \cdot {\rm Q} \left( {\varepsilon}/{\sigma} \right);\hspace{0.5cm} \text{with}\hspace{0.5cm}\sigma \approx \sqrt{{ p}/{N}}= 10^{-5}\hspace{0.05cm}, \hspace{0.3cm}\varepsilon = 5 \cdot 10^{-6}\text{:}$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr} \left( |{\rm BER} - 10^{-4}| > 0.05 \cdot 10^{-4} \right) = 2 \cdot {\rm Q} \left( \frac{5 \cdot 10^{-6}}{10^{-5}} \right) = 2 \cdot 0.309 \hspace{0.1cm}\underline {= 0.618} \hspace{0.05cm}.$$
(5) This condition can be formulated with $\varepsilon = 5 \cdot 10^{-6}$ as follows:
- $${\rm Q} \left( {\varepsilon}/{\sigma} \right) < 0.1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\varepsilon}/{\sigma} > {\rm Q}^{-1}(0.05) \approx 1.64 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{\varepsilon^2}{\sigma^2}\approx \frac{\varepsilon^2 \cdot N}{p}> 1.64^2 = 2.69$$
- $$\Rightarrow \hspace{0.3cm} N > \frac{2.69 \cdot p}{\varepsilon^2}= \frac{2.69 \cdot 10^{-4}}{25 \cdot10^{-12}}\hspace{0.1cm}\underline {\approx 10.8 \cdot 10^{6}}\hspace{0.05cm}.$$