Difference between revisions of "Aufgaben:Exercise 4.4: Maximum–a–posteriori and Maximum–Likelihood"
| (2 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver}} | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver}} | ||
| − | [[File: | + | [[File:EN_Dig_A_4_4.png|right|frame|Channel transition probabilities]] |
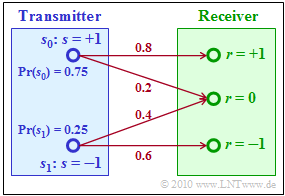
| − | To illustrate MAP and ML decision, we now construct a very simple example with only two possible messages $m_0 = 0$ and $m_1 = 1$, represented by the signal values $s_0$ | + | To illustrate "maximum–a–posteriori" $\rm (MAP)$ and "maximum likelihood" $\rm (ML)$ decision, we now construct a very simple example with only two possible messages $m_0 = 0$ and $m_1 = 1$, represented by the signal values $s_0$ resp. $s_1$: |
:$$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_0 = +1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_0 = 0\hspace{0.05cm},$$ | :$$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_0 = +1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_0 = 0\hspace{0.05cm},$$ | ||
:$$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_1 = -1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_1 = 1\hspace{0.05cm}.$$ | :$$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_1 = -1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_1 = 1\hspace{0.05cm}.$$ | ||
| Line 16: | Line 16: | ||
| − | After transmission, the | + | After transmission, the message is to be estimated by an optimal receiver. Available are: |
| − | * the '''maximum likelihood receiver''' (ML receiver), which does not know the occurrence probabilities ${\rm Pr}(s = s_i)$, with the decision rule: | + | * the '''maximum likelihood receiver''' $\rm (ML$ receiver$)$, which does not know the occurrence probabilities ${\rm Pr}(s = s_i)$, with the decision rule: |
:$$\hat{m}_{\rm ML} = {\rm arg} \max_i \hspace{0.1cm} \big[ p_{r |s } \hspace{0.05cm} (\rho | :$$\hat{m}_{\rm ML} = {\rm arg} \max_i \hspace{0.1cm} \big[ p_{r |s } \hspace{0.05cm} (\rho | ||
|s_i ) \big]\hspace{0.05cm},$$ | |s_i ) \big]\hspace{0.05cm},$$ | ||
| − | * the '''maximum-a-posteriori receiver''' (MAP receiver); this receiver also considers the symbol probabilities of the source in its decision process: | + | * the '''maximum-a-posteriori receiver''' $\rm (MAP$ receiver$)$; this receiver also considers the symbol probabilities of the source in its decision process: |
:$$\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big[ {\rm Pr}( s = s_i) \cdot p_{r |s } \hspace{0.05cm} (\rho | :$$\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big[ {\rm Pr}( s = s_i) \cdot p_{r |s } \hspace{0.05cm} (\rho | ||
|s_i ) \big ]\hspace{0.05cm}.$$ | |s_i ) \big ]\hspace{0.05cm}.$$ | ||
| Line 28: | Line 28: | ||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Optimal_Receiver_Strategies|"Optimal Receiver Strategies"]]. | ||
| + | *Reference is also made to the chapter [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver|"Structure of the Optimal Receiver]]. | ||
| − | + | * The necessary statistical principles can be found in the chapter [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence| "Statistical Dependence and Independence"]] of the book "Theory of Stochastic Signals". | |
| − | |||
| − | |||
| − | * The necessary statistical principles can be found in the chapter [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence| "Statistical Dependence and Independence"]] of the book "Theory of Stochastic Signals". | ||
| Line 75: | Line 75: | ||
{Calculate the symbol error probability of the '''ML receiver'''. | {Calculate the symbol error probability of the '''ML receiver'''. | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr(symbol error)}\ = \ $ { 0.15 3% } | + | ${\rm Pr(symbol\hspace{0.15cm} error)}\ = \ $ { 0.15 3% } |
{Calculate the symbol error probability of the '''MAP receiver'''. | {Calculate the symbol error probability of the '''MAP receiver'''. | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr(symbol error)}\ = \ $ { 0.1 3% } | + | ${\rm Pr(symbol\hspace{0.15cm}error)}\ = \ $ { 0.1 3% } |
</quiz> | </quiz> | ||
| Line 89: | Line 89: | ||
:$${\rm Pr} ( r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 - {\rm Pr} ( r = +1) - {\rm Pr} ( r = -1) = 1 - 0.6 - 0.15 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm}.$$ | :$${\rm Pr} ( r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 - {\rm Pr} ( r = +1) - {\rm Pr} ( r = -1) = 1 - 0.6 - 0.15 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm}.$$ | ||
| − | For the last probability also holds: | + | *For the last probability also holds: |
:$${\rm Pr} ( r = 0) = 0.75 \cdot 0.2 + 0.25 \cdot 0.4 = 0.25\hspace{0.05cm}.$$ | :$${\rm Pr} ( r = 0) = 0.75 \cdot 0.2 + 0.25 \cdot 0.4 = 0.25\hspace{0.05cm}.$$ | ||
| Line 97: | Line 97: | ||
= \frac{0.8 \cdot 0.75}{0.6} \hspace{0.05cm}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$ | = \frac{0.8 \cdot 0.75}{0.6} \hspace{0.05cm}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$ | ||
| − | Correspondingly, we obtain for the other probabilities: | + | *Correspondingly, we obtain for the other probabilities: |
:$${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{-0.1cm} \ = \ 1 - {\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$ | :$${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{-0.1cm} \ = \ 1 - {\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$ | ||
:$${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = -1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$ | :$${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = -1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$ | ||
| Line 105: | Line 105: | ||
| − | '''(3)''' Let $r = +1$. Then decides | + | '''(3)''' Let $r = +1$. Then decides |
| − | * the MAP receiver for $s_0$, because ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) = 1 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1)= 0\hspace{0.05cm},$ | + | * the MAP receiver for $s_0$, because ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) = 1 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1)= 0\hspace{0.05cm},$ |
| − | * the ML receiver likewise for $s_0$, since ${\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.8 > {\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0 \hspace{0.05cm}.$ | + | * the ML receiver likewise for $s_0$, since ${\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.8 > {\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0 \hspace{0.05cm}.$ |
| − | So the correct answer is <u>NO</u>. | + | So the correct answer is <u>NO</u>. |
| − | '''(4)''' <u>NO</u> is also true under the condition "$r = \, –1$", since there is no connection between $s_0$ and "$r = \, –1$". | + | '''(4)''' <u>NO</u> is also true under the condition "$r = \, –1$", since there is no connection between $s_0$ and "$r = \, –1$". |
| − | '''(5)''' <u>Solutions 1 and 4</u> are correct: | + | '''(5)''' <u>Solutions 1 and 4</u> are correct: |
| − | *The MAP receiver will choose event $s_0$, since ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.6 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.4 \hspace{0.05cm}.$ | + | *The MAP receiver will choose event $s_0$, since ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.6 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.4 \hspace{0.05cm}.$ |
| − | *In contrast, the ML receiver will choose $s_1$, since ${\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0.4 > {\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.2 \hspace{0.05cm}.$ | + | *In contrast, the ML receiver will choose $s_1$, since ${\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0.4 > {\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.2 \hspace{0.05cm}.$ |
'''(6)''' The maximum likelihood receiver | '''(6)''' The maximum likelihood receiver | ||
| − | * decides for $s_0$ only if $r = +1$, | + | * decides for $s_0$ only if $r = +1$, |
| − | * thus makes no error if $s_1$ was sent, | + | |
| − | * only makes an error when "$s_0$" and "$r = 0$" are combined: | + | * thus makes no error if $s_1$ was sent, |
| − | :$${\rm Pr} ({\rm symbol error} ) = {\rm Pr} ({\cal E } ) = 0.75 \cdot 0.2 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.15} \hspace{0.05cm}.$$ | + | |
| + | * only makes an error when "$s_0$" and "$r = 0$" are combined: | ||
| + | :$${\rm Pr} ({\rm symbol\hspace{0.15cm}error} ) = {\rm Pr} ({\cal E } ) = 0.75 \cdot 0.2 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.15} \hspace{0.05cm}.$$ | ||
| − | '''(7)''' The MAP receiver, on the other hand, decides | + | '''(7)''' The MAP receiver, on the other hand, decides for $s_0$ when "$r = 0$". So there is a symbol error only in the combination "$s_1$" and "$r = 0$". From this follows: |
| − | :$${\rm Pr} ({\rm symbol error} ) = {\rm Pr} ({\cal E } ) = 0.25 \cdot 0.4 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.1} \hspace{0.05cm}.$$ | + | :$${\rm Pr} ({\rm symbol\hspace{0.15cm}error} ) = {\rm Pr} ({\cal E } ) = 0.25 \cdot 0.4 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.1} \hspace{0.05cm}.$$ |
*The error probability here is lower than for the ML receiver, | *The error probability here is lower than for the ML receiver, | ||
| − | *because now also the different | + | *because now also the different a-priori probabilities ${\rm Pr}(s_0)$ and ${\rm Pr}(s_1)$ are considered. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 15:39, 15 July 2022
To illustrate "maximum–a–posteriori" $\rm (MAP)$ and "maximum likelihood" $\rm (ML)$ decision, we now construct a very simple example with only two possible messages $m_0 = 0$ and $m_1 = 1$, represented by the signal values $s_0$ resp. $s_1$:
- $$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_0 = +1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_0 = 0\hspace{0.05cm},$$
- $$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_1 = -1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_1 = 1\hspace{0.05cm}.$$
- Let the probabilities of occurrence be:
- $${\rm Pr}(s = s_0) = 0.75,\hspace{0.2cm}{\rm Pr}(s = s_1) = 0.25 \hspace{0.05cm}.$$
- The received signal can – for whatever reason – take three different values, i.e.
- $$r = +1,\hspace{0.2cm}r = 0,\hspace{0.2cm}r = -1 \hspace{0.05cm}.$$
- The conditional channel probabilities can be taken from the graph.
After transmission, the message is to be estimated by an optimal receiver. Available are:
- the maximum likelihood receiver $\rm (ML$ receiver$)$, which does not know the occurrence probabilities ${\rm Pr}(s = s_i)$, with the decision rule:
- $$\hat{m}_{\rm ML} = {\rm arg} \max_i \hspace{0.1cm} \big[ p_{r |s } \hspace{0.05cm} (\rho |s_i ) \big]\hspace{0.05cm},$$
- the maximum-a-posteriori receiver $\rm (MAP$ receiver$)$; this receiver also considers the symbol probabilities of the source in its decision process:
- $$\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big[ {\rm Pr}( s = s_i) \cdot p_{r |s } \hspace{0.05cm} (\rho |s_i ) \big ]\hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Optimal Receiver Strategies".
- Reference is also made to the chapter "Structure of the Optimal Receiver.
- The necessary statistical principles can be found in the chapter "Statistical Dependence and Independence" of the book "Theory of Stochastic Signals".
Questions
Solution
- $${\rm Pr} ( r = +1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} ( s_0) \cdot {\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s = +1) = 0.75 \cdot 0.8 \hspace{0.05cm}\hspace{0.15cm}\underline { = 0.6}\hspace{0.05cm},$$
- $${\rm Pr} ( r = -1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} ( s_1) \cdot {\rm Pr} ( r = -1 \hspace{0.05cm}| \hspace{0.05cm}s = -1) = 0.25 \cdot 0.6 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.15}\hspace{0.05cm},$$
- $${\rm Pr} ( r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 - {\rm Pr} ( r = +1) - {\rm Pr} ( r = -1) = 1 - 0.6 - 0.15 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm}.$$
- For the last probability also holds:
- $${\rm Pr} ( r = 0) = 0.75 \cdot 0.2 + 0.25 \cdot 0.4 = 0.25\hspace{0.05cm}.$$
(2) For the first inference probability we are looking for holds:
- $${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) = \frac{{\rm Pr} ( r = +1 \hspace{0.05cm}|\hspace{0.05cm}s_0 ) \cdot {\rm Pr} ( s_0)}{{\rm Pr} ( r = +1)} = \frac{0.8 \cdot 0.75}{0.6} \hspace{0.05cm}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$
- Correspondingly, we obtain for the other probabilities:
- $${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{-0.1cm} \ = \ 1 - {\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$
- $${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = -1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$
- $${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = -1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm},$$
- $${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{{\rm Pr} ( r = 0 \hspace{0.05cm}|\hspace{0.05cm}s_0 ) \cdot {\rm Pr} ( s_0)}{{\rm Pr} ( r = 0 )}= \frac{0.2 \cdot 0.75}{0.25} \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.6}\hspace{0.05cm},$$
- $${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1- {\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.4} \hspace{0.05cm}.$$
(3) Let $r = +1$. Then decides
- the MAP receiver for $s_0$, because ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) = 1 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1)= 0\hspace{0.05cm},$
- the ML receiver likewise for $s_0$, since ${\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.8 > {\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0 \hspace{0.05cm}.$
So the correct answer is NO.
(4) NO is also true under the condition "$r = \, –1$", since there is no connection between $s_0$ and "$r = \, –1$".
(5) Solutions 1 and 4 are correct:
- The MAP receiver will choose event $s_0$, since ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.6 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.4 \hspace{0.05cm}.$
- In contrast, the ML receiver will choose $s_1$, since ${\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0.4 > {\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.2 \hspace{0.05cm}.$
(6) The maximum likelihood receiver
- decides for $s_0$ only if $r = +1$,
- thus makes no error if $s_1$ was sent,
- only makes an error when "$s_0$" and "$r = 0$" are combined:
- $${\rm Pr} ({\rm symbol\hspace{0.15cm}error} ) = {\rm Pr} ({\cal E } ) = 0.75 \cdot 0.2 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.15} \hspace{0.05cm}.$$
(7) The MAP receiver, on the other hand, decides for $s_0$ when "$r = 0$". So there is a symbol error only in the combination "$s_1$" and "$r = 0$". From this follows:
- $${\rm Pr} ({\rm symbol\hspace{0.15cm}error} ) = {\rm Pr} ({\cal E } ) = 0.25 \cdot 0.4 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.1} \hspace{0.05cm}.$$
- The error probability here is lower than for the ML receiver,
- because now also the different a-priori probabilities ${\rm Pr}(s_0)$ and ${\rm Pr}(s_1)$ are considered.