Difference between revisions of "Aufgaben:Exercise 4.10: Union Bound"
From LNTwww
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Approximation_of_the_Error_Probability}} |
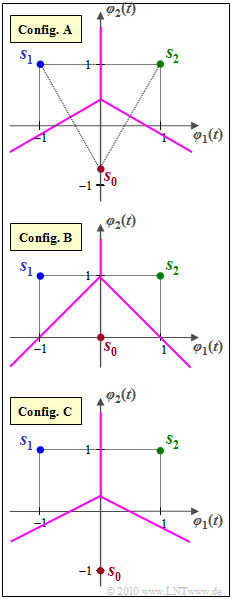
| − | [[File: | + | [[File:EN_Dig_A_4_10.png|right|frame|Signal space constellations with $N=2$ and $M=3$]] |
| − | + | The so-called "Union Bound" gives an upper bound for the error probability of a non-binary transmission system $(M > 2)$. | |
| − | + | *The actual (average) error probability is generally given as follows: | |
:$${\rm Pr}({ \cal E}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sum\limits_{i = 0 }^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{0.05cm},$$ | :$${\rm Pr}({ \cal E}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sum\limits_{i = 0 }^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{0.05cm},$$ | ||
| − | :$$ {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} \left [ \bigcup_{k \ne i} { \cal E}_{ik}\right ] \hspace{0.05cm},\hspace{0.2cm}{ \rm | + | :$$ {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} \left [ \bigcup_{k \ne i} { \cal E}_{ik}\right ] \hspace{0.05cm},\hspace{0.2cm}{ \rm where}\hspace{0.2cm} |
| − | { \cal E}_{ik}\text{:} \ \ \boldsymbol{ r }{\rm \hspace{0.15cm} | + | { \cal E}_{ik}\text{:} \ \ \boldsymbol{ r }{\rm \hspace{0.15cm}is \hspace{0.15cm}closer \hspace{0.15cm}to \hspace{0.15cm}}\boldsymbol{ s }_k {\rm \hspace{0.15cm}than \hspace{0.15cm}to \hspace{0.15cm}the \hspace{0.15cm}setpoint \hspace{0.15cm}}\boldsymbol{ s }_i |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *The simpler "Union Bound" $\rm (UB)$ provides an upper bound on the falsification probability assuming that message $m_i$ $($or signal $\boldsymbol{s}_i)$ was sent: | |
:$$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ \ge \ \hspace{-0.1cm} {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s }_i ) = {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i )\hspace{0.05cm},\ $$ | :$$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ \ge \ \hspace{-0.1cm} {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s }_i ) = {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i )\hspace{0.05cm},\ $$ | ||
:$$ p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ = \ \hspace{-0.2cm}\sum\limits_{k = 0 ,\hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm} | :$$ p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ = \ \hspace{-0.2cm}\sum\limits_{k = 0 ,\hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm} | ||
{\rm Pr}({ \cal E}_{ik}) = \hspace{-0.1cm}\sum\limits_{k = 0, \hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm}{\rm Q} \left ( \frac{d_{ik}/2}{\sigma_n} \right )\hspace{0.05cm}. $$ | {\rm Pr}({ \cal E}_{ik}) = \hspace{-0.1cm}\sum\limits_{k = 0, \hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm}{\rm Q} \left ( \frac{d_{ik}/2}{\sigma_n} \right )\hspace{0.05cm}. $$ | ||
| − | + | The following abbreviations are used: | |
| − | * ${\rm Q}(x)$ | + | * ${\rm Q}(x)$ is the complementary Gaussian error function; |
| − | |||
| − | |||
| + | * $d_{ik}$ denotes the distance between the signal points $\boldsymbol{s}_i$ and $\boldsymbol{s}_k$; | ||
| − | + | * $\sigma_n$ is the rms value (⇒ root of the variance) of the additive white Gaussian noise. | |
| + | |||
| + | |||
| + | ⇒ By averaging over all possible signals $\boldsymbol{s}_i$, we then arrive at the actual "Union Bound": | ||
:$$p_{\rm UB} = \sum\limits_{i = 0 }^{M-1} {\rm Pr}(\boldsymbol{ s }_i) \cdot p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \ge {\rm Pr}({ \cal E}) \hspace{0.05cm}.$$ | :$$p_{\rm UB} = \sum\limits_{i = 0 }^{M-1} {\rm Pr}(\boldsymbol{ s }_i) \cdot p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \ge {\rm Pr}({ \cal E}) \hspace{0.05cm}.$$ | ||
| − | * | + | *The graph shows three different signal space constellations, <br>each with $M = 3$ signal space points $\boldsymbol{s}_0$, $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$ in two-dimensional space $(N = 2)$. |
| − | * | + | |
| − | * | + | *The basis functions $\varphi_1(t)$ and $\varphi_2(t)$ are suitably normalized. |
| + | |||
| + | *Thus, the signal space coordinates are also pure numerical values without unit: | ||
:$$\boldsymbol{ s }_1 = (-1, \hspace{0.1cm}+1)\hspace{0.05cm}, \hspace{0.2cm} | :$$\boldsymbol{ s }_1 = (-1, \hspace{0.1cm}+1)\hspace{0.05cm}, \hspace{0.2cm} | ||
\boldsymbol{ s }_2 = (+1, \hspace{0.1cm}+1)\hspace{0.05cm}.$$ | \boldsymbol{ s }_2 = (+1, \hspace{0.1cm}+1)\hspace{0.05cm}.$$ | ||
| − | * | + | *The signal space point $\boldsymbol{s}_0$ in configuration $\rm A$ is located such that $\boldsymbol{s}_0$, $\boldsymbol{s}_1$, $\boldsymbol{s}_2$ describe an equilateral triangle. |
| + | |||
| + | *In contrast, in configurations $\rm B$ and $\rm C$, $\boldsymbol{s}_0 = (0,\ 0)$ resp. $\boldsymbol{s}_0 = (0, \ –1)$. | ||
| Line 37: | Line 43: | ||
| − | + | Notes: | |
| − | * | + | * The exercise belongs to the chapter [[Digital_Signal_Transmission/Approximation_of_the_Error_Probability|"Approximation of the Error Probability"]]. |
| − | * | + | |
| + | *Use the AWGN rms value $\sigma_n = 0.5$ for all calculations. | ||
| − | * | + | * Given the following values of the complementary Gaussian error function: |
:$${\rm Q}(1) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.159\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(\sqrt{2}) \approx 0.079\hspace{0.05cm}, \hspace{0.23cm}{\rm Q}(\sqrt{3}) \approx 0.042\hspace{0.05cm},$$ | :$${\rm Q}(1) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.159\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(\sqrt{2}) \approx 0.079\hspace{0.05cm}, \hspace{0.23cm}{\rm Q}(\sqrt{3}) \approx 0.042\hspace{0.05cm},$$ | ||
:$${\rm Q}(2) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.023\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.14) \approx 0.016\hspace{0.05cm}, \hspace{0.1cm}{\rm Q}(\sqrt{5}) \approx 0.013 \hspace{0.05cm}.$$ | :$${\rm Q}(2) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.023\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.14) \approx 0.016\hspace{0.05cm}, \hspace{0.1cm}{\rm Q}(\sqrt{5}) \approx 0.013 \hspace{0.05cm}.$$ | ||
| Line 47: | Line 54: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the three configurations leads to the smallest error probability $($at least according to the Union Bound approximation$)$? |
|type="()"} | |type="()"} | ||
| − | - | + | - Configuration $\rm A$, |
| − | - | + | - Configuration $\rm B$, |
| − | + | + | + Configuration $\rm C$. |
| − | { | + | {Calculate the "averaged Union Bound" $(p_{\rm UB})$ for configuration $\rm A$. |
|type="{}"} | |type="{}"} | ||
$p_{\rm UB} \ = \ ${ 4.6 3% } $\ \%$ | $p_{\rm UB} \ = \ ${ 4.6 3% } $\ \%$ | ||
| − | { | + | {Calculate the "averaged Union Bound" for configuration $\rm B$. |
|type="{}"} | |type="{}"} | ||
$p_{\rm UB} \ = \ ${ 12.1 3% } $\ \%$ | $p_{\rm UB} \ = \ ${ 12.1 3% } $\ \%$ | ||
| − | { | + | {Calculate the "averaged Union Bound" for configuration $\rm C$. |
|type="{}"} | |type="{}"} | ||
$p_{\rm UB} \ = \ ${ 3.2 3% } $\ \%$ | $p_{\rm UB} \ = \ ${ 3.2 3% } $\ \%$ | ||
| − | { | + | {How would the noise rms value $\sigma_n$ have to be changed for configuration $\rm A$ to yield the same "Union Bound" as in subtask '''(4)'''? |
|type="{}"} | |type="{}"} | ||
$\sigma_n \ = \ ${ 0.467 3% } | $\sigma_n \ = \ ${ 0.467 3% } | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Points $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$ are the same for all configurations. |
| − | * | + | *The smallest error probability occurs when $\boldsymbol{s}_0$ is farthest from $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$. |
| − | * | + | |
| + | *This is the case for configuration $\rm C$ ⇒ <u>solution 3</u>. | ||
| + | |||
| + | '''(2)''' For configuration $\rm A$, the distance between all points is the same: $d_{01} = d_{02} = d_{12} = 2$. | ||
| + | *Therefore, to calculate the "Union Bound", it is not necessary to average over all symbols. | ||
| − | + | *And it is valid since e.g. $\boldsymbol{s}_0$ is distorted into symbol $\boldsymbol{s}_1$ or $\boldsymbol{s}_2$ with equal probability: | |
| − | |||
:$${\rm Pr}({ \cal E}) \le p_{\rm UB} = 2 \cdot {\rm Q} \left ( \frac{d_{ik}/2}{\sigma_n} \right ) = 2 \cdot {\rm Q}(2) \approx 2 \cdot 0.023 \hspace{0.1cm}\hspace{0.15cm}\underline {= 4.6\%} \hspace{0.05cm}. $$ | :$${\rm Pr}({ \cal E}) \le p_{\rm UB} = 2 \cdot {\rm Q} \left ( \frac{d_{ik}/2}{\sigma_n} \right ) = 2 \cdot {\rm Q}(2) \approx 2 \cdot 0.023 \hspace{0.1cm}\hspace{0.15cm}\underline {= 4.6\%} \hspace{0.05cm}. $$ | ||
| − | '''(3)''' | + | '''(3)''' Here, the falsification probabilities differ for each symbol. |
| − | * | + | *If $\boldsymbol{s}_0$ was sent, with $d_{01} = d_{02} = 2^{0.5}$ and $\sigma = 0.5$: |
:$$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_0} = 2 \cdot {\rm Q} \left ( \frac{\sqrt{2}/2}{0.5} \right ) | :$$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_0} = 2 \cdot {\rm Q} \left ( \frac{\sqrt{2}/2}{0.5} \right ) | ||
= 2 \cdot {\rm Q}(\sqrt{2}) = 2 \cdot 0.079 = 0.158 \hspace{0.05cm}. $$ | = 2 \cdot {\rm Q}(\sqrt{2}) = 2 \cdot 0.079 = 0.158 \hspace{0.05cm}. $$ | ||
| − | * | + | *In contrast, the other two conditional probabilities are smaller: |
:$$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_1} = p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} | :$$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_1} = p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} | ||
{\rm Q} \left ( \frac{{2}/2}{0.5} \right )+{\rm Q} \left ( \frac{\sqrt{2}/2}{0.5} \right )= {\rm Q}(2) +{\rm Q}(\sqrt{2}) = 0.023 + 0.079 = 0.102 \hspace{0.05cm}.$$ | {\rm Q} \left ( \frac{{2}/2}{0.5} \right )+{\rm Q} \left ( \frac{\sqrt{2}/2}{0.5} \right )= {\rm Q}(2) +{\rm Q}(\sqrt{2}) = 0.023 + 0.079 = 0.102 \hspace{0.05cm}.$$ | ||
| − | + | *By averaging, we obtain for the Union Bound considering the different distances: | |
:$$p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{3} \cdot \left [ p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_0} + p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_1} +p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_2}\right ]= | :$$p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{3} \cdot \left [ p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_0} + p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_1} +p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_2}\right ]= | ||
{1}/{3} \cdot \left [ 2 \cdot {\rm Q}(\sqrt{2})+ 2 \cdot ({\rm Q}({2}) + {\rm Q}(\sqrt{2})) \right ] = | {1}/{3} \cdot \left [ 2 \cdot {\rm Q}(\sqrt{2})+ 2 \cdot ({\rm Q}({2}) + {\rm Q}(\sqrt{2})) \right ] = | ||
{1}/{3} \cdot \left [ 4 \cdot {\rm Q}(\sqrt{2})+ 2 \cdot {\rm Q}({2}) \right ] $$ | {1}/{3} \cdot \left [ 4 \cdot {\rm Q}(\sqrt{2})+ 2 \cdot {\rm Q}({2}) \right ] $$ | ||
:$$ \Rightarrow \hspace{0.3cm} p_{\rm UB} = | :$$ \Rightarrow \hspace{0.3cm} p_{\rm UB} = | ||
| − | {1}/{3} \cdot \ | + | {1}/{3} \cdot \big [ 4 \cdot 0.079+ 2 \cdot 0.023 \big ] \hspace{0.1cm}\hspace{0.12cm}\underline {\approx 12.1\% } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm UB}\ge {\rm Pr}({ \cal E})\hspace{0.05cm}.$$ |
| − | '''(4)''' | + | '''(4)''' This configuration is described by the following equations: |
:$$d_{01} = d_{02} = \sqrt{2^2 + 1^2}= \sqrt{5} \approx 2.24\hspace{0.2cm}, d_{12} = 2$$ | :$$d_{01} = d_{02} = \sqrt{2^2 + 1^2}= \sqrt{5} \approx 2.24\hspace{0.2cm}, d_{12} = 2$$ | ||
:$$\Rightarrow \hspace{0.3cm} p_{\rm UB} = | :$$\Rightarrow \hspace{0.3cm} p_{\rm UB} = | ||
| − | {1}/{3} \cdot \ | + | {1}/{3} \cdot \big [ 4 \cdot {\rm Q}(\sqrt{5})+ 2 \cdot {\rm Q}({2}) \big ] = {1}/{3} \cdot \big [ 4 \cdot 0.013+ 2 \cdot 0.023 \big ]\hspace{0.1cm}\hspace{0.15cm}\underline {\approx 3.2\%} \hspace{0.05cm}. $$ |
| − | '''(5)''' | + | '''(5)''' Let it be: |
:$$p_{\rm UB} = 2 \cdot {\rm Q}\left ( {1}/{\sigma_n} \right ) = 0.032 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | :$$p_{\rm UB} = 2 \cdot {\rm Q}\left ( {1}/{\sigma_n} \right ) = 0.032 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
{\rm Q}\left ( {1}/{\sigma_n} \right ) = 0.016\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {1}/{\sigma_n} \approx 2.14 | {\rm Q}\left ( {1}/{\sigma_n} \right ) = 0.016\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {1}/{\sigma_n} \approx 2.14 | ||
Latest revision as of 16:13, 6 September 2022
The so-called "Union Bound" gives an upper bound for the error probability of a non-binary transmission system $(M > 2)$.
- The actual (average) error probability is generally given as follows:
- $${\rm Pr}({ \cal E}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sum\limits_{i = 0 }^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{0.05cm},$$
- $$ {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} \left [ \bigcup_{k \ne i} { \cal E}_{ik}\right ] \hspace{0.05cm},\hspace{0.2cm}{ \rm where}\hspace{0.2cm} { \cal E}_{ik}\text{:} \ \ \boldsymbol{ r }{\rm \hspace{0.15cm}is \hspace{0.15cm}closer \hspace{0.15cm}to \hspace{0.15cm}}\boldsymbol{ s }_k {\rm \hspace{0.15cm}than \hspace{0.15cm}to \hspace{0.15cm}the \hspace{0.15cm}setpoint \hspace{0.15cm}}\boldsymbol{ s }_i \hspace{0.05cm}.$$
- The simpler "Union Bound" $\rm (UB)$ provides an upper bound on the falsification probability assuming that message $m_i$ $($or signal $\boldsymbol{s}_i)$ was sent:
- $$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ \ge \ \hspace{-0.1cm} {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s }_i ) = {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i )\hspace{0.05cm},\ $$
- $$ p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ = \ \hspace{-0.2cm}\sum\limits_{k = 0 ,\hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm} {\rm Pr}({ \cal E}_{ik}) = \hspace{-0.1cm}\sum\limits_{k = 0, \hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm}{\rm Q} \left ( \frac{d_{ik}/2}{\sigma_n} \right )\hspace{0.05cm}. $$
The following abbreviations are used:
- ${\rm Q}(x)$ is the complementary Gaussian error function;
- $d_{ik}$ denotes the distance between the signal points $\boldsymbol{s}_i$ and $\boldsymbol{s}_k$;
- $\sigma_n$ is the rms value (⇒ root of the variance) of the additive white Gaussian noise.
⇒ By averaging over all possible signals $\boldsymbol{s}_i$, we then arrive at the actual "Union Bound":
- $$p_{\rm UB} = \sum\limits_{i = 0 }^{M-1} {\rm Pr}(\boldsymbol{ s }_i) \cdot p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \ge {\rm Pr}({ \cal E}) \hspace{0.05cm}.$$
- The graph shows three different signal space constellations,
each with $M = 3$ signal space points $\boldsymbol{s}_0$, $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$ in two-dimensional space $(N = 2)$.
- The basis functions $\varphi_1(t)$ and $\varphi_2(t)$ are suitably normalized.
- Thus, the signal space coordinates are also pure numerical values without unit:
- $$\boldsymbol{ s }_1 = (-1, \hspace{0.1cm}+1)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_2 = (+1, \hspace{0.1cm}+1)\hspace{0.05cm}.$$
- The signal space point $\boldsymbol{s}_0$ in configuration $\rm A$ is located such that $\boldsymbol{s}_0$, $\boldsymbol{s}_1$, $\boldsymbol{s}_2$ describe an equilateral triangle.
- In contrast, in configurations $\rm B$ and $\rm C$, $\boldsymbol{s}_0 = (0,\ 0)$ resp. $\boldsymbol{s}_0 = (0, \ –1)$.
Notes:
- The exercise belongs to the chapter "Approximation of the Error Probability".
- Use the AWGN rms value $\sigma_n = 0.5$ for all calculations.
- Given the following values of the complementary Gaussian error function:
- $${\rm Q}(1) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.159\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(\sqrt{2}) \approx 0.079\hspace{0.05cm}, \hspace{0.23cm}{\rm Q}(\sqrt{3}) \approx 0.042\hspace{0.05cm},$$
- $${\rm Q}(2) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.023\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.14) \approx 0.016\hspace{0.05cm}, \hspace{0.1cm}{\rm Q}(\sqrt{5}) \approx 0.013 \hspace{0.05cm}.$$
Questions
Solution
(1) Points $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$ are the same for all configurations.
- The smallest error probability occurs when $\boldsymbol{s}_0$ is farthest from $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$.
- This is the case for configuration $\rm C$ ⇒ solution 3.
(2) For configuration $\rm A$, the distance between all points is the same: $d_{01} = d_{02} = d_{12} = 2$.
- Therefore, to calculate the "Union Bound", it is not necessary to average over all symbols.
- And it is valid since e.g. $\boldsymbol{s}_0$ is distorted into symbol $\boldsymbol{s}_1$ or $\boldsymbol{s}_2$ with equal probability:
- $${\rm Pr}({ \cal E}) \le p_{\rm UB} = 2 \cdot {\rm Q} \left ( \frac{d_{ik}/2}{\sigma_n} \right ) = 2 \cdot {\rm Q}(2) \approx 2 \cdot 0.023 \hspace{0.1cm}\hspace{0.15cm}\underline {= 4.6\%} \hspace{0.05cm}. $$
(3) Here, the falsification probabilities differ for each symbol.
- If $\boldsymbol{s}_0$ was sent, with $d_{01} = d_{02} = 2^{0.5}$ and $\sigma = 0.5$:
- $$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_0} = 2 \cdot {\rm Q} \left ( \frac{\sqrt{2}/2}{0.5} \right ) = 2 \cdot {\rm Q}(\sqrt{2}) = 2 \cdot 0.079 = 0.158 \hspace{0.05cm}. $$
- In contrast, the other two conditional probabilities are smaller:
- $$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_1} = p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Q} \left ( \frac{{2}/2}{0.5} \right )+{\rm Q} \left ( \frac{\sqrt{2}/2}{0.5} \right )= {\rm Q}(2) +{\rm Q}(\sqrt{2}) = 0.023 + 0.079 = 0.102 \hspace{0.05cm}.$$
- By averaging, we obtain for the Union Bound considering the different distances:
- $$p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{3} \cdot \left [ p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_0} + p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_1} +p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_2}\right ]= {1}/{3} \cdot \left [ 2 \cdot {\rm Q}(\sqrt{2})+ 2 \cdot ({\rm Q}({2}) + {\rm Q}(\sqrt{2})) \right ] = {1}/{3} \cdot \left [ 4 \cdot {\rm Q}(\sqrt{2})+ 2 \cdot {\rm Q}({2}) \right ] $$
- $$ \Rightarrow \hspace{0.3cm} p_{\rm UB} = {1}/{3} \cdot \big [ 4 \cdot 0.079+ 2 \cdot 0.023 \big ] \hspace{0.1cm}\hspace{0.12cm}\underline {\approx 12.1\% } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm UB}\ge {\rm Pr}({ \cal E})\hspace{0.05cm}.$$
(4) This configuration is described by the following equations:
- $$d_{01} = d_{02} = \sqrt{2^2 + 1^2}= \sqrt{5} \approx 2.24\hspace{0.2cm}, d_{12} = 2$$
- $$\Rightarrow \hspace{0.3cm} p_{\rm UB} = {1}/{3} \cdot \big [ 4 \cdot {\rm Q}(\sqrt{5})+ 2 \cdot {\rm Q}({2}) \big ] = {1}/{3} \cdot \big [ 4 \cdot 0.013+ 2 \cdot 0.023 \big ]\hspace{0.1cm}\hspace{0.15cm}\underline {\approx 3.2\%} \hspace{0.05cm}. $$
(5) Let it be:
- $$p_{\rm UB} = 2 \cdot {\rm Q}\left ( {1}/{\sigma_n} \right ) = 0.032 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q}\left ( {1}/{\sigma_n} \right ) = 0.016\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {1}/{\sigma_n} \approx 2.14 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.1cm}\hspace{0.15cm}\sigma_n \hspace{0.15cm}\underline {\approx 0.467}\hspace{0.05cm}. $$