Difference between revisions of "Aufgaben:Exercise 5.2: Error Correlation Function"
| (2 intermediate revisions by 2 users not shown) | |||
| Line 41: | Line 41: | ||
${\rm E}\big[a\big] \ = \ ${ 10 3% } | ${\rm E}\big[a\big] \ = \ ${ 10 3% } | ||
| − | {Calculate the value of the error correlation function \rm (ECF)$ for $k = 1$. | + | {Calculate the value of the error correlation function $\rm (ECF)$ for $k = 1$. |
|type="{}"} | |type="{}"} | ||
$\varphi_e(k = 1) \ = \ ${ 0.0309 3% } | $\varphi_e(k = 1) \ = \ ${ 0.0309 3% } | ||
| Line 52: | Line 52: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The mean probability | + | '''(1)''' The mean error probability is equal to the ECF value for $k = 0$. Namely, because of $e_{\nu} ∈ \{0, 1\}$: |
:$$\varphi_{e}(k = 0) = {\rm E}[e_{\nu}^2 ]= {\rm E}[e_{\nu} ]= | :$$\varphi_{e}(k = 0) = {\rm E}[e_{\nu}^2 ]= {\rm E}[e_{\nu} ]= | ||
p_{\rm M} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm M}\hspace{0.15cm}\underline { = 0.1} | p_{\rm M} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm M}\hspace{0.15cm}\underline { = 0.1} | ||
| Line 58: | Line 58: | ||
| − | '''(2)''' The mean error distance is equal to the reciprocal of the mean error probability. That is: | + | '''(2)''' The mean $($or: "average"$)$ error distance is equal to the reciprocal of the mean error probability. That is: |
:$${\rm E}\big[a\big] = 1/p_{\rm M} \ \underline {= 10}.$$ | :$${\rm E}\big[a\big] = 1/p_{\rm M} \ \underline {= 10}.$$ | ||
| − | '''(3)''' According to the definition equation and [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence#Conditional_Probability| "Bayes' theorem"]], the following result is obtained: | + | '''(3)''' According to the definition equation and [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence#Conditional_Probability| "Bayes' theorem"]], the following result is obtained: |
:$$\varphi_{e}(k = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm | :$$\varphi_{e}(k = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm | ||
E}[e_{\nu} \cdot e_{\nu + 1}] = {\rm E}[(e_{\nu} = 1) \cdot | E}[e_{\nu} \cdot e_{\nu + 1}] = {\rm E}[(e_{\nu} = 1) \cdot | ||
| Line 70: | Line 70: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The first probability is equal to ${\rm Pr}(a = 1)$ and the second probability is equal to $p_{\rm M}$: | + | *The first probability is equal to ${\rm Pr}(a = 1)$ and the second probability is equal to $p_{\rm M}$: |
| − | :$$\varphi_{e}(k = 1) = 0.3091 \cdot 0.1\hspace{0.15cm}\underline { = 0.0309} | + | :$$\varphi_{e}(k = 1) = {\rm Pr}(a = 1) \cdot p_{\rm M} = 0.3091 \cdot 0.1\hspace{0.15cm}\underline { = 0.0309} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(4)''' The ECF value $\varphi_e(k = 2)$ can be interpreted (approximately) as follows: | + | '''(4)''' The ECF value $\varphi_e(k = 2)$ can be interpreted (approximately) as follows: |
:$$\varphi_{e}(k = 2) ={\rm Pr}(e_{\nu + 2}=1 | :$$\varphi_{e}(k = 2) ={\rm Pr}(e_{\nu + 2}=1 | ||
| − | \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) \cdot p_{\rm M} | + | \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) \cdot p_{\rm M} $$ |
| − | \Rightarrow \hspace{0.3cm}{\rm Pr}(e_{\nu + 2}=1 | + | :$$\Rightarrow \hspace{0.3cm}{\rm Pr}(e_{\nu + 2}=1 |
\hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) = \frac{\varphi_{e}(k | \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) = \frac{\varphi_{e}(k | ||
= 2)}{p_{\rm M}} = \frac{0.0267}{0.1} = 0.267\hspace{0.05cm}.$$ | = 2)}{p_{\rm M}} = \frac{0.0267}{0.1} = 0.267\hspace{0.05cm}.$$ | ||
| − | This probability is composed of " | + | *This probability is composed of "at time $\nu+1$ an error occurs" and "at time $\nu+1$ there is no error": |
:$${\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = | :$${\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = | ||
1) = {\rm Pr}( a =1) \cdot {\rm Pr}( a =1) + {\rm Pr}( a =2)\hspace{0.3cm} | 1) = {\rm Pr}( a =1) \cdot {\rm Pr}( a =1) + {\rm Pr}( a =2)\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}{\rm Pr}( a =2)= 0.267 - 0.3091^2 \hspace{0.15cm}\underline {= 0.1715}\hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm}{\rm Pr}( a =2)= 0.267 - 0.3091^2 \hspace{0.15cm}\underline {= 0.1715}\hspace{0.05cm}.$$ | ||
| − | In the calculation, it was assumed that the individual error distances are statistically independent of each other. | + | *In the calculation, it was assumed that the individual error distances are statistically independent of each other. |
| − | + | #However, this assumption is valid only for a special class of channel models called "renewing". | |
| − | + | #The burst error model considered here does not satisfy this condition. | |
| − | + | #The actual probability ${\rm Pr}(a = 2) = 0.1675$ therefore deviates slightly from the value calculated here $(0.1715)$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Digital Signal Transmission: Exercises|^5.1 Digital Channel Models^]] | [[Category:Digital Signal Transmission: Exercises|^5.1 Digital Channel Models^]] | ||
Latest revision as of 03:39, 18 September 2022
For the characterization of digital channel models one uses among other things
- the "error correlation function" $\rm (ECF)$
- $$\varphi_{e}(k) = {\rm E}\big[e_{\nu} \cdot e_{\nu + k}\big]\hspace{0.05cm}, \hspace{0.2cm} k \ge 0\hspace{0.05cm},$$
- the "error distance probabilities"
- $${\rm Pr}( a =k) \hspace{0.05cm}, \hspace{0.2cm} k \ge 1\hspace{0.05cm}.$$
Here denote:
- $〈e_{\rm \nu}〉$ is the error sequence with $e_{\rm \nu} ∈ \{0, 1\}$.
- $a$ indicates the error distance with $a_{\rm \nu} ∈ \{0, 1, 2, \text{...} \}$.
Two directly consecutive symbol errors are thus characterized by the error distance $a = 1$.
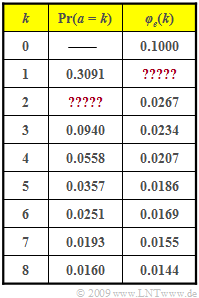
The table shows exemplary values of the error distance probabilities ${\rm Pr}(a = k)$ as well as the error correlation function $\varphi_e(k)$.
- Some data are missing in the table.
- These values are to be calculated from the given values.
Note: The exercise covers the subject matter of the chapter "Parameters of Digital Channel Models".
Questions
Solution
- $$\varphi_{e}(k = 0) = {\rm E}[e_{\nu}^2 ]= {\rm E}[e_{\nu} ]= p_{\rm M} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm M}\hspace{0.15cm}\underline { = 0.1} \hspace{0.05cm}.$$
(2) The mean $($or: "average"$)$ error distance is equal to the reciprocal of the mean error probability. That is:
- $${\rm E}\big[a\big] = 1/p_{\rm M} \ \underline {= 10}.$$
(3) According to the definition equation and "Bayes' theorem", the following result is obtained:
- $$\varphi_{e}(k = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm E}[e_{\nu} \cdot e_{\nu + 1}] = {\rm E}[(e_{\nu} = 1) \cdot (e_{\nu + 1}=1)]={\rm Pr}(e_{\nu + 1}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) \cdot {\rm Pr}(e_{\nu} = 1) \hspace{0.05cm}.$$
- The first probability is equal to ${\rm Pr}(a = 1)$ and the second probability is equal to $p_{\rm M}$:
- $$\varphi_{e}(k = 1) = {\rm Pr}(a = 1) \cdot p_{\rm M} = 0.3091 \cdot 0.1\hspace{0.15cm}\underline { = 0.0309} \hspace{0.05cm}.$$
(4) The ECF value $\varphi_e(k = 2)$ can be interpreted (approximately) as follows:
- $$\varphi_{e}(k = 2) ={\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) \cdot p_{\rm M} $$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) = \frac{\varphi_{e}(k = 2)}{p_{\rm M}} = \frac{0.0267}{0.1} = 0.267\hspace{0.05cm}.$$
- This probability is composed of "at time $\nu+1$ an error occurs" and "at time $\nu+1$ there is no error":
- $${\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) = {\rm Pr}( a =1) \cdot {\rm Pr}( a =1) + {\rm Pr}( a =2)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}( a =2)= 0.267 - 0.3091^2 \hspace{0.15cm}\underline {= 0.1715}\hspace{0.05cm}.$$
- In the calculation, it was assumed that the individual error distances are statistically independent of each other.
- However, this assumption is valid only for a special class of channel models called "renewing".
- The burst error model considered here does not satisfy this condition.
- The actual probability ${\rm Pr}(a = 2) = 0.1675$ therefore deviates slightly from the value calculated here $(0.1715)$.