Difference between revisions of "Aufgaben:Exercise 3.6: State Transition Diagram"
From LNTwww
| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
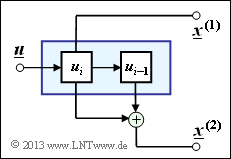
[[File:P_ID2648__KC_A_3_6.png|right|frame|Simple realization of a rate $1/2$ convolutional encoder]] | [[File:P_ID2648__KC_A_3_6.png|right|frame|Simple realization of a rate $1/2$ convolutional encoder]] | ||
| − | A description possibility for convolutional | + | A description possibility for convolutional encoders is provided by the so-called "state transition diagram". |
| + | *If the encoder contains $m$ memory registers ⇒ influence length $\nu = m + 1$, then there are different states $S_{\mu}$ with $0 ≤ \mu ≤ 2^m -1$, where holds for the index: | ||
:$$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2^{l-1} \cdot u_{i-l} | :$$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2^{l-1} \cdot u_{i-l} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | This type of code description is to be applied to the convolutional coder of rate $R = 1/2$ outlined above. | + | *This type of code description is to be applied to the convolutional coder of rate $R = 1/2$ outlined above. |
| − | |||
| − | |||
| − | |||
| + | <u>Hints:</u> | ||
| + | *This exercise belongs to the chapter [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram| "Code Description with State and Trellis Diagram"]]. | ||
| − | |||
| − | |||
*Reference is made in particular to the section [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#State_definition_for_a_memory_register|"State definition for a memory register"]]. | *Reference is made in particular to the section [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#State_definition_for_a_memory_register|"State definition for a memory register"]]. | ||
| Line 34: | Line 32: | ||
{What statements hold for the transition from $s_i = S_1$ to $s_{i+1} = S_0$? | {What statements hold for the transition from $s_i = S_1$ to $s_{i+1} = S_0$? | ||
|type="[]"} | |type="[]"} | ||
| − | + The current information bit must $u_i = 0$ . | + | + The current information bit must be $u_i = 0$ . |
- The current information bit must be $u_i = 1$ . | - The current information bit must be $u_i = 1$ . | ||
+ The associated code sequence is $\underline{x}_i = (01)$. | + The associated code sequence is $\underline{x}_i = (01)$. | ||
| Line 41: | Line 39: | ||
{What statements hold for the transition from $s_i = S_1$ to $s_{i+1} = S_1$? | {What statements hold for the transition from $s_i = S_1$ to $s_{i+1} = S_1$? | ||
|type="[]"} | |type="[]"} | ||
| − | - The current information bit must $u_i = 0$ . | + | - The current information bit must be $u_i = 0$ . |
+ The current information bit must be $u_i = 1$ . | + The current information bit must be $u_i = 1$ . | ||
- The associated code sequence is $\underline{x}_i = (01)$. | - The associated code sequence is $\underline{x}_i = (01)$. | ||
| Line 60: | Line 58: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
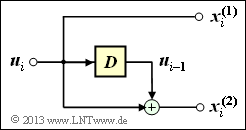
[[File:P_ID2649__KC_A_3_6a_neu.png|right|frame|Equivalent circuit diagram of the encoder under consideration]] | [[File:P_ID2649__KC_A_3_6a_neu.png|right|frame|Equivalent circuit diagram of the encoder under consideration]] | ||
| − | '''(1)''' As can be seen from the accompanying equivalent circuit diagram, the encoder contains only one memory element <br>⇒ | + | '''(1)''' As can be seen from the accompanying equivalent circuit diagram, the encoder contains only one memory element <br>⇒ memory $m = 1$. Thus there are $2^m \ \underline{= 2}$ states, viz. |
* the state $S_0 \ \Rightarrow \ u_{i–1} = 0$, | * the state $S_0 \ \Rightarrow \ u_{i–1} = 0$, | ||
| + | |||
* the state $S_1 \ \Rightarrow \ u_{i–1} = 1$. | * the state $S_1 \ \Rightarrow \ u_{i–1} = 1$. | ||
| − | '''(2)''' From each state $2^k = 2$ arrows | + | '''(2)''' From each state go $2^k = 2$ arrows to different states. |
| − | *Since there are only two states, the answer <u>YES</u> is correct. | + | *Since there are only two states, the answer <u>YES</u> is correct. |
| − | '''(3)''' Correct are the <u>solutions 1 and 3</u>: | + | '''(3)''' Correct are the <u>solutions 1 and 3</u>: |
| − | *The information bit $u_i$ present at time $i$ is | + | *The information bit $u_i$ present at time $i$ is with respect to the following time $(j = i + 1)$ the previous bit $(u_{j–1})$. |
| − | *Thus $s_{i+1} = u_i$ holds. Only with $u_i = 0$ does one get from $s_i = S_1$ to $s_{i+1} = S_0$ ⇒ <u>Proposed solution 1</u>. | + | |
| − | *From $s_i = S_1$ ⇒ $u_{i–1} = 1$ follows further ⇒ <u>Proposed solution 3</u>: | + | *Thus $s_{i+1} = u_i$ holds. Only with $u_i = 0$ does one get from $s_i = S_1$ to $s_{i+1} = S_0$ ⇒ <u>Proposed solution 1</u>. |
| + | |||
| + | *From $s_i = S_1$ ⇒ $u_{i–1} = 1$ follows further ⇒ <u>Proposed solution 3</u>: | ||
:$${x}_i^{(1)} = u_i = 0\hspace{0.05cm},\hspace{0.2cm}{x}_i^{(2)} = u_i + u_{i-1}= 0+1 = 1 | :$${x}_i^{(1)} = u_i = 0\hspace{0.05cm},\hspace{0.2cm}{x}_i^{(2)} = u_i + u_{i-1}= 0+1 = 1 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\underline{x}_i = (0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\underline{x}_i = (0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | *The proposed solution 4 could have been ruled out from the beginning. The graph on the specification sheet clearly shows that the coder is systematic: $x_i^{(1)} = u_i$. The combination $u_i = 0$ and $\underline{x}_i = (1, 0)$ would contradict this. | + | *The proposed solution 4 could have been ruled out from the beginning. The graph on the specification sheet clearly shows that the coder is systematic: $x_i^{(1)} = u_i$. |
| + | |||
| + | *The combination $u_i = 0$ and $\underline{x}_i = (1, 0)$ would contradict this. | ||
| + | |||
| + | |||
| + | |||
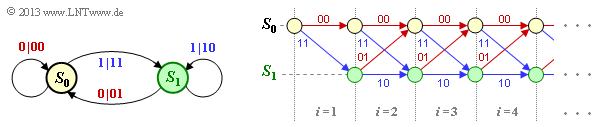
| + | [[File:P_ID2650__KC_A_3_6d.png|right|frame|State and trellis diagram for the encoder under consideration]] | ||
| + | '''(4)''' Correct are the <u>solutions 2 and 4</u>: | ||
| + | *Using a similar solution path as in subtask '''(3)''', one arrives at the result that the current information bit must be $u_i = 1$. | ||
| + | *The corresponding code sequence is $\underline{x}_i = (10)$. | ||
| + | |||
| + | *This results in the following state transition diagram $($left$)$ and the trellis diagram that can be derived from it: | ||
| + | *Red arrows indicate the information bit $u_i = 0$, while blue arrows indicate $u_i = 1$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(5)''' <u>Both proposed solutions</u> are correct. There are no other constraints $($except binary$)$ for the information sequences. | ||
| − | |||
| + | '''(6)''' Correct is the <u>proposed solution 1</u>. Starting from the state $S_0$ one comes | ||
| + | * with $u_1 = 1$ to the state $S_1$, output "$11$", | ||
| + | * with $u_2 = 1$ to the state $S_1$, output "$10$", | ||
| + | * with $u_3 = 0$ to state $S_0$, output "$01$", | ||
| + | * with $u_4 = 0$ to state $S_0$, output "$00$", | ||
| + | * with $u_5 = 1$ to state $S_1$, output "$11$", | ||
| + | * with $u_6 = 1$ to the state $S_1$, output "$10$". | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | In contrast, the second code sequence is not possible: | ||
| + | * The output "$11$" means that one started at $S_0$ and comes with $u_1 = 1$ to the state $S_1$. | ||
| − | + | * But in the state $S_1$ then only the outputs "$01$" and "$10$" are possible, but not "$00$". | |
| − | |||
| − | * But in the state $S_1$ then only the outputs "$01$" and "$10$" are possible, but not "$00$". | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 14:42, 12 November 2022
A description possibility for convolutional encoders is provided by the so-called "state transition diagram".
- If the encoder contains $m$ memory registers ⇒ influence length $\nu = m + 1$, then there are different states $S_{\mu}$ with $0 ≤ \mu ≤ 2^m -1$, where holds for the index:
- $$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2^{l-1} \cdot u_{i-l} \hspace{0.05cm}.$$
- This type of code description is to be applied to the convolutional coder of rate $R = 1/2$ outlined above.
Hints:
- This exercise belongs to the chapter "Code Description with State and Trellis Diagram".
- Reference is made in particular to the section "State definition for a memory register".
Questions
Solution
(1) As can be seen from the accompanying equivalent circuit diagram, the encoder contains only one memory element
⇒ memory $m = 1$. Thus there are $2^m \ \underline{= 2}$ states, viz.
- the state $S_0 \ \Rightarrow \ u_{i–1} = 0$,
- the state $S_1 \ \Rightarrow \ u_{i–1} = 1$.
(2) From each state go $2^k = 2$ arrows to different states.
- Since there are only two states, the answer YES is correct.
(3) Correct are the solutions 1 and 3:
- The information bit $u_i$ present at time $i$ is with respect to the following time $(j = i + 1)$ the previous bit $(u_{j–1})$.
- Thus $s_{i+1} = u_i$ holds. Only with $u_i = 0$ does one get from $s_i = S_1$ to $s_{i+1} = S_0$ ⇒ Proposed solution 1.
- From $s_i = S_1$ ⇒ $u_{i–1} = 1$ follows further ⇒ Proposed solution 3:
- $${x}_i^{(1)} = u_i = 0\hspace{0.05cm},\hspace{0.2cm}{x}_i^{(2)} = u_i + u_{i-1}= 0+1 = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\underline{x}_i = (0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \hspace{0.05cm}. $$
- The proposed solution 4 could have been ruled out from the beginning. The graph on the specification sheet clearly shows that the coder is systematic: $x_i^{(1)} = u_i$.
- The combination $u_i = 0$ and $\underline{x}_i = (1, 0)$ would contradict this.
(4) Correct are the solutions 2 and 4:
- Using a similar solution path as in subtask (3), one arrives at the result that the current information bit must be $u_i = 1$.
- The corresponding code sequence is $\underline{x}_i = (10)$.
- This results in the following state transition diagram $($left$)$ and the trellis diagram that can be derived from it:
- Red arrows indicate the information bit $u_i = 0$, while blue arrows indicate $u_i = 1$.
(5) Both proposed solutions are correct. There are no other constraints $($except binary$)$ for the information sequences.
(6) Correct is the proposed solution 1. Starting from the state $S_0$ one comes
- with $u_1 = 1$ to the state $S_1$, output "$11$",
- with $u_2 = 1$ to the state $S_1$, output "$10$",
- with $u_3 = 0$ to state $S_0$, output "$01$",
- with $u_4 = 0$ to state $S_0$, output "$00$",
- with $u_5 = 1$ to state $S_1$, output "$11$",
- with $u_6 = 1$ to the state $S_1$, output "$10$".
In contrast, the second code sequence is not possible:
- The output "$11$" means that one started at $S_0$ and comes with $u_1 = 1$ to the state $S_1$.
- But in the state $S_1$ then only the outputs "$01$" and "$10$" are possible, but not "$00$".