Difference between revisions of "Aufgaben:Exercise 4.2: Channel Log Likelihood Ratio at AWGN"
From LNTwww
| (3 intermediate revisions by the same user not shown) | |||
| Line 43: | Line 43: | ||
{What are the characteristics of the channels shown in the diagram? | {What are the characteristics of the channels shown in the diagram? | ||
|type="[]"} | |type="[]"} | ||
| − | + They describe the binary transmission under Gaussian | + | + They describe the binary transmission under Gaussian noise. |
+ The bit error probability without coding is ${\rm Q}(1/\sigma)$. | + The bit error probability without coding is ${\rm Q}(1/\sigma)$. | ||
| − | + The channel | + | + The channel log likelihood ratio is given as $L_{\rm K}(y) = K_{\rm L} \cdot y$. |
| − | {Which constant $K_{\rm L}$ characterizes the channel $\rm A$? | + | {Which constant $K_{\rm L}$ characterizes the channel $\rm A$? |
|type="{}"} | |type="{}"} | ||
$K_{\rm L} \ = \ ${ 2 3% } | $K_{\rm L} \ = \ ${ 2 3% } | ||
| − | {For channel $\rm A$ what information do the received values $y_1 = 1, \ y_2 = 0.5$, $y_3 = \, -1.5$ provide about the transmitted binary symbols $x_1, \ x_2$ and $x_3$ | + | {For channel $\rm A$ what information do the received values $y_1 = 1, \ y_2 = 0.5$, $y_3 = \, -1.5$ provide about the transmitted binary symbols $x_1, \ x_2$ and $x_3$? |
|type="[]"} | |type="[]"} | ||
+ $y_1 = 1.0$ states that probably $x_1 = +1$ was sent. | + $y_1 = 1.0$ states that probably $x_1 = +1$ was sent. | ||
+ $y_2 = 0.5$ states that probably $x_2 = +1$ was sent. | + $y_2 = 0.5$ states that probably $x_2 = +1$ was sent. | ||
+ $y_3 = \, -1.5$ states that probably $x_3 = \, -1$ was sent. | + $y_3 = \, -1.5$ states that probably $x_3 = \, -1$ was sent. | ||
| − | + The decision "$y_1 → x_1$" is | + | + The decision "$y_1 → x_1$" is safer than "$y_2 → x_2$". |
- The decision "$y_1 → x_1$" is safer than "$y_3 → x_3$". | - The decision "$y_1 → x_1$" is safer than "$y_3 → x_3$". | ||
| Line 63: | Line 63: | ||
$K_{\rm L} \ = \ ${ 8 3% } | $K_{\rm L} \ = \ ${ 8 3% } | ||
| − | {What information does channel $\rm B$ provide about the received values $y_1 = 1, \ y_2 = 0.5$, $y_3 = -1.5$ about the transmitted binary symbols $x_1, \ x_2$ | + | {What information does channel $\rm B$ provide about the received values $y_1 = 1, \ y_2 = 0.5$, $y_3 = -1.5$ about the transmitted binary symbols $x_1, \ x_2$ and $x_3$? |
|type="[]"} | |type="[]"} | ||
+ For $x_1, \ x_2, \ x_3$ is decided the same as for channel $\rm A$. | + For $x_1, \ x_2, \ x_3$ is decided the same as for channel $\rm A$. | ||
+ The estimate "$x_2 = +1$" is four times more certain than for channel $\rm A$. | + The estimate "$x_2 = +1$" is four times more certain than for channel $\rm A$. | ||
| − | - The estimate "$x_3 = \, -1$" at channel $\rm A$ is more reliable than the estimate "$x_2 = +1$" at channel $\rm B$. | + | - The estimate "$x_3 = \, -1$" at channel $\rm A$ is more reliable than the estimate "$x_2 = +1$" at channel $\rm B$. |
</quiz> | </quiz> | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u>All proposed solutions</u> are correct: | + | '''(1)''' <u>All proposed solutions</u> are correct: |
| − | * The transfer equation is always $y = x + n$, with $x ∈ \{+1, \, -1\}$ | + | * The transfer equation is always $y = x + n$, with $x ∈ \{+1, \, -1\}$. |
| − | |||
| − | |||
| − | |||
| + | *The variable $n$ is a Gaussian random variable with standard deviation $\sigma$ ⇒ variance $\sigma^2$ ⇒ [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_Binary_Input| "AWGN Channel"]]. | ||
| − | '''(2)''' For the AWGN channel | + | * The [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission#Error_probability_with_Gaussian_noise|"AWGN bit error probability"]] is calculated using the standard deviation $\sigma$ to ${\rm Q}(1/\sigma)$ where ${\rm Q}(x)$ denotes the [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Exceedance_probability|"complementary Gaussian error function"]]. |
| + | |||
| + | * For each AWGN channel, according to the [[Channel_Coding/Soft-in_Soft-Out_Decoder#Reliability_information_-_Log_Likelihood_Ratio|"theory section"]], the channel log likelihood ratio always results in $L_{\rm K}(y) = L(y|x) = K_{\rm L} \cdot y$. | ||
| + | |||
| + | *The constant $K_{\rm L}$ is different for the two channels. | ||
| + | |||
| + | |||
| + | '''(2)''' For the AWGN channel ⇒ $L_{\rm K}(y) = K_{\rm L} \cdot y$ with constant $K_{\rm L} = 2/\sigma^2$. | ||
| + | *The standard deviation $\sigma$ can be read from the graph on the data page as the distance of the inflection points within the Gaussian curves from their respective midpoints. For '''channel A''' ⇒ $\sigma = 1$ results. | ||
*The same result is obtained by evaluating the Gaussian function | *The same result is obtained by evaluating the Gaussian function | ||
:$$\frac{f_{\rm G}( y = \sigma)}{f_{\rm G}( y = 0)} = {\rm e} ^{ - y^2/(2\sigma^2) } \Bigg |_{\hspace{0.05cm} y \hspace{0.05cm} = \hspace{0.05cm} \sigma} = {\rm e} ^{ -0.5} \approx 0.6065\hspace{0.05cm}.$$ | :$$\frac{f_{\rm G}( y = \sigma)}{f_{\rm G}( y = 0)} = {\rm e} ^{ - y^2/(2\sigma^2) } \Bigg |_{\hspace{0.05cm} y \hspace{0.05cm} = \hspace{0.05cm} \sigma} = {\rm e} ^{ -0.5} \approx 0.6065\hspace{0.05cm}.$$ | ||
| − | *This means: At the abscissa value $y = \sigma$ the mean-free Gaussian function $f_{\rm G}(y)$ has decayed to $60.65\%$ of its maximum value. Thus, for the constant at '''channel A''': $K_{\rm L} = 2/\sigma^2 \ \underline{= 2}$. | + | *This means: At the abscissa value $y = \sigma$ the mean-free Gaussian function $f_{\rm G}(y)$ has decayed to $60.65\%$ of its maximum value. |
| + | |||
| + | *Thus, for the constant at '''channel A''': $K_{\rm L} = 2/\sigma^2 \ \underline{= 2}$. | ||
| − | '''(3)''' | + | '''(3)''' Correct are the <u>solutions 1 to 4</u>: |
| − | *We first give the respective | + | *We first give the respective log likelihood ratios of '''Channel A''': |
:$$L_{\rm K}(y_1 = +1.0) = +2\hspace{0.05cm},\hspace{0.3cm} | :$$L_{\rm K}(y_1 = +1.0) = +2\hspace{0.05cm},\hspace{0.3cm} | ||
L_{\rm K}(y_2 = +0.5) = +1\hspace{0.05cm},\hspace{0.3cm} | L_{\rm K}(y_2 = +0.5) = +1\hspace{0.05cm},\hspace{0.3cm} | ||
L_{\rm K}(y_3 = -1.5) = -3\hspace{0.05cm}. $$ | L_{\rm K}(y_3 = -1.5) = -3\hspace{0.05cm}. $$ | ||
*This results in the following consequences: | *This results in the following consequences: | ||
| − | # The decision for the (most probable) | + | # The decision for the $($most probable$)$ code bit $x_i$ is based on the sign of $L_{\rm K}(y_i)$: <br> $x_1 = +1, \ x_2 = +1, \ x_3 = \, -1$ ⇒ the <u>proposed solutions 1, 2 and 3</u> are correct. |
| − | # The decision "$x_1 = +1$" is more reliable than the decision "$x_2 = +1$" ⇒ <u>Proposition 4</u> is also correct. | + | # The decision "$x_1 = +1$" is more reliable than the decision "$x_2 = +1$" ⇒ <u>Proposition 4</u> is also correct. |
| − | # However, the decision "$x_1 = +1$" is less reliable than the decision "$x_3 = \, –1$" because $|L_{\rm K}(y_1) | + | # However, the decision "$x_1 = +1$" is less reliable than the decision "$x_3 = \, –1$" because $|L_{\rm K}(y_1)<|L_{\rm K}(y_3)|$ ⇒ proposed solution 5 is incorrect. |
| − | |||
| − | This can also be interpreted as follows: The quotient between the red and the blue PDF value at $y_3 = \, -1.5$ is larger than the quotient between the blue and the red PDF value at $y_1 = +1$. | + | *This can also be interpreted as follows: The quotient between the red and the blue PDF value at $y_3 = \, -1.5$ is larger than the quotient between the blue and the red PDF value at $y_1 = +1$. |
| − | '''(4)''' Following the same considerations as in subtask (2), the | + | '''(4)''' Following the same considerations as in subtask '''(2)''', the standard deviation of '''channel B''' is given by: |
| + | :$$\sigma = 1/2 \ \Rightarrow \ K_{\rm L} = 2/\sigma^2 \ \underline{= 8}.$$ | ||
| − | '''(5)''' For '''channel B''', the following applies: $L_{\rm K}(y_1 = +1.0) = +8, \ L_{\rm K}(y_2 = +0.5) = +4 | + | '''(5)''' For '''channel B''', the following applies: |
| + | :$$L_{\rm K}(y_1 = +1.0) = +8, \ L_{\rm K}(y_2 = +0.5) = +4, \ L_{\rm K}(y_3 = \, -1.5) = \, -12.$$ | ||
| − | *It is obvious that <u>the first two proposed solutions</u> are true, but not the third, because | + | *It is obvious that <u>the first two proposed solutions</u> are true, but not the third, because |
:$$|L_{\rm K}(y_3 = -1.5, {\rm channel\hspace{0.15cm} A)}| = 3 | :$$|L_{\rm K}(y_3 = -1.5, {\rm channel\hspace{0.15cm} A)}| = 3 | ||
| − | \hspace{0. | + | \hspace{0.2cm} <\hspace{0.2cm} |
|L_{\rm K}(y_2 = 0.5, {\rm channel\hspace{0.15cm} B)}| = 4\hspace{0.05cm} . $$ | |L_{\rm K}(y_2 = 0.5, {\rm channel\hspace{0.15cm} B)}| = 4\hspace{0.05cm} . $$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 15:21, 29 November 2022
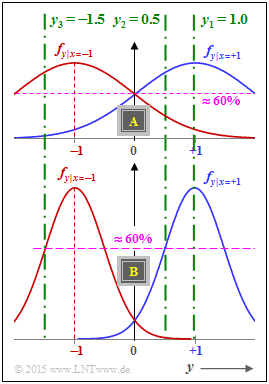
We consider two channels $\rm A$ and $\rm B$, each with
- binary bipolar input $x ∈ \{+1, \, -1\}$, and
- continuous-valued output $y ∈ {\rm \mathcal{R}}$ (real number).
The graph shows for both channels
- as blue curve the probability density functions $f_{y\hspace{0.05cm}|\hspace{0.05cm}x=+1}$,
- as red curve the probability density functions $f_{y\hspace{0.05cm}|\hspace{0.05cm}x=-1}$.
In the "theory section" the channel $($German: "Kanal" ⇒ subscript: "K"$)$ log likelihood ratio was derived for this AWGN constellation as follows:
- $$L_{\rm K}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=+1) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = -1)} \hspace{0.05cm}.$$
Evaluating this equation analytically, we obtain with the proportionality constant $K_{\rm L} = 2/\sigma^2$:
- $$L_{\rm K}(y) = K_{\rm L} \cdot y \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the sections
Questions
Solution
(1) All proposed solutions are correct:
- The transfer equation is always $y = x + n$, with $x ∈ \{+1, \, -1\}$.
- The variable $n$ is a Gaussian random variable with standard deviation $\sigma$ ⇒ variance $\sigma^2$ ⇒ "AWGN Channel".
- The "AWGN bit error probability" is calculated using the standard deviation $\sigma$ to ${\rm Q}(1/\sigma)$ where ${\rm Q}(x)$ denotes the "complementary Gaussian error function".
- For each AWGN channel, according to the "theory section", the channel log likelihood ratio always results in $L_{\rm K}(y) = L(y|x) = K_{\rm L} \cdot y$.
- The constant $K_{\rm L}$ is different for the two channels.
(2) For the AWGN channel ⇒ $L_{\rm K}(y) = K_{\rm L} \cdot y$ with constant $K_{\rm L} = 2/\sigma^2$.
- The standard deviation $\sigma$ can be read from the graph on the data page as the distance of the inflection points within the Gaussian curves from their respective midpoints. For channel A ⇒ $\sigma = 1$ results.
- The same result is obtained by evaluating the Gaussian function
- $$\frac{f_{\rm G}( y = \sigma)}{f_{\rm G}( y = 0)} = {\rm e} ^{ - y^2/(2\sigma^2) } \Bigg |_{\hspace{0.05cm} y \hspace{0.05cm} = \hspace{0.05cm} \sigma} = {\rm e} ^{ -0.5} \approx 0.6065\hspace{0.05cm}.$$
- This means: At the abscissa value $y = \sigma$ the mean-free Gaussian function $f_{\rm G}(y)$ has decayed to $60.65\%$ of its maximum value.
- Thus, for the constant at channel A: $K_{\rm L} = 2/\sigma^2 \ \underline{= 2}$.
(3) Correct are the solutions 1 to 4:
- We first give the respective log likelihood ratios of Channel A:
- $$L_{\rm K}(y_1 = +1.0) = +2\hspace{0.05cm},\hspace{0.3cm} L_{\rm K}(y_2 = +0.5) = +1\hspace{0.05cm},\hspace{0.3cm} L_{\rm K}(y_3 = -1.5) = -3\hspace{0.05cm}. $$
- This results in the following consequences:
- The decision for the $($most probable$)$ code bit $x_i$ is based on the sign of $L_{\rm K}(y_i)$:
$x_1 = +1, \ x_2 = +1, \ x_3 = \, -1$ ⇒ the proposed solutions 1, 2 and 3 are correct. - The decision "$x_1 = +1$" is more reliable than the decision "$x_2 = +1$" ⇒ Proposition 4 is also correct.
- However, the decision "$x_1 = +1$" is less reliable than the decision "$x_3 = \, –1$" because $|L_{\rm K}(y_1)<|L_{\rm K}(y_3)|$ ⇒ proposed solution 5 is incorrect.
- This can also be interpreted as follows: The quotient between the red and the blue PDF value at $y_3 = \, -1.5$ is larger than the quotient between the blue and the red PDF value at $y_1 = +1$.
(4) Following the same considerations as in subtask (2), the standard deviation of channel B is given by:
- $$\sigma = 1/2 \ \Rightarrow \ K_{\rm L} = 2/\sigma^2 \ \underline{= 8}.$$
(5) For channel B, the following applies:
- $$L_{\rm K}(y_1 = +1.0) = +8, \ L_{\rm K}(y_2 = +0.5) = +4, \ L_{\rm K}(y_3 = \, -1.5) = \, -12.$$
- It is obvious that the first two proposed solutions are true, but not the third, because
- $$|L_{\rm K}(y_3 = -1.5, {\rm channel\hspace{0.15cm} A)}| = 3 \hspace{0.2cm} <\hspace{0.2cm} |L_{\rm K}(y_2 = 0.5, {\rm channel\hspace{0.15cm} B)}| = 4\hspace{0.05cm} . $$