Difference between revisions of "Applets:Frequency & Impulse Responses"
m (Text replacement - "Biographies_and_Bibliographies/LNTwww_members_from_LNT#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28at_LNT_since_1974.29" to "Biographies_and_Bibliographies/LNTwww_members_from_LNT#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28at_LNT_from_1974-2024.29") |
|||
| (22 intermediate revisions by 3 users not shown) | |||
| Line 5: | Line 5: | ||
<br> | <br> | ||
| − | Real and symmetric low- | + | Real and symmetric low-pass frquency responses $H(f)$ and the corresponding impulse responses $h(t)$ are shown, namely |
#Gaussian low-pass, | #Gaussian low-pass, | ||
#rectangular low-pass, | #rectangular low-pass, | ||
#triangular low-pass, | #triangular low-pass, | ||
#trapezoidal low-pass, | #trapezoidal low-pass, | ||
| − | #cosine rolloff low-pass ⇒ | + | #cosine rolloff low-pass ⇒ »raised-cosine low-pass«, |
| − | #cosine rolloff squared low-pass ⇒ | + | #cosine rolloff squared low-pass ⇒ »cosine-square low-pass«. |
| Line 29: | Line 29: | ||
===Frequency response $H(f)$ and impulse response $h(t)$=== | ===Frequency response $H(f)$ and impulse response $h(t)$=== | ||
| − | *The [[Linear_and_Time_Invariant_Systems/System_Description_in_Frequency_Domain#Frequency_response_.E2.80.93_Transfer_function| | + | *The [[Linear_and_Time_Invariant_Systems/System_Description_in_Frequency_Domain#Frequency_response_.E2.80.93_Transfer_function|$\text{frequency response}$]] $($or the "transfer function"$)$ $H(f)$ of a linear time-invariant transmission system gives the ratio between the output spectrum $Y(f)$ and that of the input spectrum $X(f)$: |
:$$H(f) = \frac{Y(f)}{X(f)}.$$ | :$$H(f) = \frac{Y(f)}{X(f)}.$$ | ||
| − | *If the transmission behavior at low frequencies is better than at higher frequencies, it is called a '''low-pass'''. | + | *If the transmission behavior at low frequencies is better than at higher frequencies, it is called a »'''low-pass'''«. |
| − | *The properties of $H(f)$ are expressed in the time domain by the [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain#Impulse_response| | + | *The properties of $H(f)$ are expressed in the time domain by the [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain#Impulse_response|$\text{impulse response}$]] $h(t)$. According to the [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|$\text{second Fourier integral}$]] holds: |
:$$h(t)={\rm IFT} [H(f)] = \int_{-\infty}^{+\infty}H(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} | :$$h(t)={\rm IFT} [H(f)] = \int_{-\infty}^{+\infty}H(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} | ||
{\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fourier \ transform.$$ | {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fourier \ transform.$$ | ||
| − | *The inverse direction is described by the [[Signal_Representation/ | + | *The inverse direction is described by the [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|$\text{first Fourier integral}$]]: |
:$$H(f)={\rm FT} [h(t)] = \int_{-\infty}^{+\infty}h(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} | :$$H(f)={\rm FT} [h(t)] = \int_{-\infty}^{+\infty}h(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} | ||
\rm FT\hspace{-0.1cm}: \ Fourier\ transform.$$ | \rm FT\hspace{-0.1cm}: \ Fourier\ transform.$$ | ||
| Line 45: | Line 45: | ||
*The unit of impulse response is $\rm 1/s$. It is true that $\rm 1/s = 1 \ Hz$, but the unit "Hertz" is unusual in this context. | *The unit of impulse response is $\rm 1/s$. It is true that $\rm 1/s = 1 \ Hz$, but the unit "Hertz" is unusual in this context. | ||
| − | *The relationship between this applet and the similarly constructed applet [[Applets:Pulses_and_Spectra|"Pulses and Spectra"]] is based on the [[Signal_Representation/ | + | *The relationship between this applet and the similarly constructed applet [[Applets:Pulses_and_Spectra|"Pulses and Spectra"]] is based on the [[Signal_Representation/Fourier_Transform_Theorems#Duality_Theorem|$\text{Duality Theorem}$]]. |
*All times are normalized to a normalization time $T$ and all frequencies are normalized to $1/T \ \Rightarrow$ the numerical values of $h(t)$ still have to be divided by $T$. | *All times are normalized to a normalization time $T$ and all frequencies are normalized to $1/T \ \Rightarrow$ the numerical values of $h(t)$ still have to be divided by $T$. | ||
| Line 72: | Line 72: | ||
:$$h(t)=K\cdot \Delta f \cdot {\rm e}^{-\pi(t\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f)^2} .$$ | :$$h(t)=K\cdot \Delta f \cdot {\rm e}^{-\pi(t\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f)^2} .$$ | ||
| − | *The smaller $\Delta f$, the wider and lower is the impulse response ⇒ [[Signal_Representation/ | + | *The smaller $\Delta f$, the wider and lower is the impulse response ⇒ [[Signal_Representation/Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|$\text{Reciprocity theorem of bandwidth and impulse duration}$]]. |
*Both $H(f)$ and $h(t)$ are not exactly equal to zero at any value of $f$ resp. $t$. | *Both $H(f)$ and $h(t)$ are not exactly equal to zero at any value of $f$ resp. $t$. | ||
| Line 82: | Line 82: | ||
===Rectangular low-pass === | ===Rectangular low-pass === | ||
*The rectangular low-pass with height $K$ and $($equivalent$)$ bandwidth $\Delta f$ reads: | *The rectangular low-pass with height $K$ and $($equivalent$)$ bandwidth $\Delta f$ reads: | ||
| − | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{ | + | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f/2,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| = \Delta f/2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ \end{array}$$ |
*The $\pm \Delta f/2$ value lies midway between the left-hand and right-hand limits. | *The $\pm \Delta f/2$ value lies midway between the left-hand and right-hand limits. | ||
| Line 99: | Line 99: | ||
:$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \Big(1-\frac{|f|}{\Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$ | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \Big(1-\frac{|f|}{\Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$ | ||
*The absolute physical bandwidth $B$ ⇒ [positive frequencies only] is also equal $\Delta f$, thus is as large as for the rectangular low-pass. | *The absolute physical bandwidth $B$ ⇒ [positive frequencies only] is also equal $\Delta f$, thus is as large as for the rectangular low-pass. | ||
| − | |||
*For the impulse response $h(t)$ one obtains according to the second Fourier transform: | *For the impulse response $h(t)$ one obtains according to the second Fourier transform: | ||
| − | :$$h(t)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta f \cdot t) \quad \text{with} \quad {\rm si}(x)={\sin(x)}/{x}.$$ | + | :$$h(t)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta f \cdot t) \quad \text{with} \quad {\rm si}(x)={\sin(x)}/{x}={\rm sinc}(x/\pi).$$ |
*$H(f)$ can be represented as a convolution of two rectangular functions $($each with width $\Delta f)$. | *$H(f)$ can be represented as a convolution of two rectangular functions $($each with width $\Delta f)$. | ||
| − | *It follows: $h(t)$ contains instead of the ${\rm si}$–function the ${\rm si}^2$–function. | + | *It follows: $h(t)$ contains instead of the ${\rm si}$–function the ${\rm si}^2$–function. |
*$h(t)$ thus also exhibits zeros at equidistant intervals $1/\Delta f$. | *$h(t)$ thus also exhibits zeros at equidistant intervals $1/\Delta f$. | ||
| Line 117: | Line 116: | ||
*The trapezoidal low-pass with height $K$ and the two corner frequencies $f_1$ and $f_2$ reads: | *The trapezoidal low-pass with height $K$ and the two corner frequencies $f_1$ and $f_2$ reads: | ||
:$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{f_2-|f|}{f_2-f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$ | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{f_2-|f|}{f_2-f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$ | ||
| − | |||
| − | |||
*For the equivalent bandwidth $($equal-area rectangle$)$ the following applies: $\Delta f = f_1+f_2$. | *For the equivalent bandwidth $($equal-area rectangle$)$ the following applies: $\Delta f = f_1+f_2$. | ||
| Line 133: | Line 130: | ||
===Cosine rolloff low-pass === | ===Cosine rolloff low-pass === | ||
| − | <u>Note:</u> In English-language literature, this filter is often also referred to as ''' | + | <u>Note:</u> In English-language literature, this filter is often also referred to as »'''raised-cosine low-pass'''«. |
*The cosine-rolloff low-pass with height $K$ and the two corner frequencies $f_1$ and $f_2$ reads: | *The cosine-rolloff low-pass with height $K$ and the two corner frequencies $f_1$ and $f_2$ reads: | ||
:$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|f|-f_1}{f_2-f_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$ | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|f|-f_1}{f_2-f_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$ | ||
| − | |||
| − | |||
| − | |||
*For the equivalent bandwidth $($equal-area rectangle$)$ the following applies: $\Delta f = f_1+f_2$. | *For the equivalent bandwidth $($equal-area rectangle$)$ the following applies: $\Delta f = f_1+f_2$. | ||
| Line 159: | Line 153: | ||
:$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|f|\hspace{0.05cm}\cdot\hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$ | :$$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|f|\hspace{0.05cm}\cdot\hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$ | ||
| − | * | + | *For the impulse response one obtains according to the Fourier inverse transform: |
| − | :$$h(t)=K\cdot \Delta f \cdot {\pi}/{4}\cdot \big [{\rm | + | :$$h(t)=K\cdot \Delta f \cdot {\pi}/{4}\cdot \big [{\rm sinc}(\Delta f\cdot t +0.5)+{\rm sinc}(\Delta f\cdot t -0.5)\big ]\cdot {\rm sinc}(\Delta f \cdot t)\quad \text{with} \quad {\rm sinc}(x)={\sin(x)}/{(\pi x})={\rm si}(\pi x).$$ |
| − | * | + | |
| − | * | + | *Because of the last ${\rm sinc}$–function, $h(t)=0$ for all multiples of $T=1/\Delta f$ ⇒ The equidistant zero crossings of the cosine rolloff low-pass are preserved. |
| − | * | + | *Due to the expression in parentheses, $h(t)$ now shows further zero crossings at $t=\pm1.5 T$, $\pm2.5 T$, $\pm3.5 T$, ... |
| − | * | + | *For $t=\pm T/2$ the impulse response has the value $K\cdot \Delta f/2$. |
| + | *The asymptotic decay of $h(t)$ runs in this special case with $1/t^3$. | ||
==Exercises== | ==Exercises== | ||
| Line 177: | Line 172: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(1)''' Compare the <b>red Gaussian | + | '''(1)''' Compare the »<b>red Gaussian low-pass</b>« $(K_1 = 1, \Delta f_1 = 1)$ to the »<b>blue rectangular low-pass</b>« $(K_2 = 1, \Delta f_2 = 1)$. Questions:<br> |
'''(a)''' Which output signals $y(t)$ result from the signal $x(t) = 2 \cdot \cos (2\pi f_0 t -\varphi_0)$ with $f_0 = 0.5$?<br> | '''(a)''' Which output signals $y(t)$ result from the signal $x(t) = 2 \cdot \cos (2\pi f_0 t -\varphi_0)$ with $f_0 = 0.5$?<br> | ||
| − | '''(b)''' What are the differences between the two | + | '''(b)''' What are the differences between the two low-pass filters with $f_0 = 0.5 \pm f_\varepsilon$ and $f_\varepsilon \ne 0, \ f_\varepsilon \to 0$?}} |
:'''(a)''' It holds $y(t) = A \cdot \cos (2\pi f_0 t -\varphi_0)$ with $A = 2 \cdot H(f = f_0) \ \Rightarrow \ A_1 = 0.912, \ A_2 = 1,000$. The phase $\varphi_0$ remains unchanged.<br> | :'''(a)''' It holds $y(t) = A \cdot \cos (2\pi f_0 t -\varphi_0)$ with $A = 2 \cdot H(f = f_0) \ \Rightarrow \ A_1 = 0.912, \ A_2 = 1,000$. The phase $\varphi_0$ remains unchanged.<br> | ||
| Line 186: | Line 181: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(2)''' Leave the settings unchanged. Which | + | '''(2)''' Leave the settings unchanged. Which low-pass $H(f)$ fulfills the first or the second Nyquist criterion?<br> Here $H(f)$ denotes the total frequency response of transmitter, |
| − | channel and | + | channel and recettion filter.}} |
* First Nyquist criterion: The impulse response $h(t)$ must have equidistant zero crossings at the (normalized) times $t = 1,\ 2$, ... <br> | * First Nyquist criterion: The impulse response $h(t)$ must have equidistant zero crossings at the (normalized) times $t = 1,\ 2$, ... <br> | ||
| − | * The impulse response $h(t) = {\rm | + | * The impulse response $h(t) = {\rm sinc}(\delta f \cdot t)$ of the rectangular low-pass filter fulfils this criterion with $\Delta f = 1$. <br> |
| − | * In contrast, the first Nyquist criterion is never fulfilled for the Gaussian | + | * In contrast, the first Nyquist criterion is never fulfilled for the Gaussian low-pass and there is always impulse interference.<br> |
| − | * The second Nyquist criterion is met by neither the rectangular | + | * The second Nyquist criterion is met by neither the rectangular low-pass nor the Gaussian low-pass. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(3)''' Compare the <b>red rectangular | + | '''(3)''' Compare the »<b>red rectangular low-pass</b>« $(K_1 = 0.5, \Delta f_1 = 2)$ to the »<b>blue rectangular low-pass</b>« $(K_2 = 1, \Delta f_2 = 1)$. Then vary $\Delta f_1$ between $2$ ... $0.5$.}} |
* With $\Delta f_1 = 2$ the zeros of $h_1(t)$ are multiples of $0.5$ ⇒ $h_1(t)$ will decay twice as fast as $h_2(t)$. <br> | * With $\Delta f_1 = 2$ the zeros of $h_1(t)$ are multiples of $0.5$ ⇒ $h_1(t)$ will decay twice as fast as $h_2(t)$. <br> | ||
| Line 204: | Line 199: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(4)''' Compare the <b>red trapezoidal | + | '''(4)''' Compare the »<b>red trapezoidal low-pass</b>« $(K_1 = 1, \ \Delta f_1 = 1, \ r_1 = 0.5)$ with »<b>blue rectangular low-pass</b>« $(K_2 = 1, \ \Delta f_2 = 1)$. $r_1$ varies between $0$ ... $1$. }} |
* With $r_1 = 0.5$ the followers/precursors of $h_1(t)$ for the "trapezoid" are less than for the "rectangle" due to the flatter edge drop .<br> | * With $r_1 = 0.5$ the followers/precursors of $h_1(t)$ for the "trapezoid" are less than for the "rectangle" due to the flatter edge drop .<br> | ||
| − | * With smaller $r_1$ followers & precursors increase. With $r_1= 0$ the trapezoidal is equal to the rectangular | + | * With smaller $r_1$ followers & precursors increase. With $r_1= 0$ the trapezoidal is equal to the rectangular low-pass ⇒ $h(t)= {\rm si}(\pi \cdot t/T)$. <br> |
| − | * With larger $r_1$ followers & precursors become smaller. With $r_1= 1$ the trapezoidal is equal to the triangular | + | * With larger $r_1$ followers & precursors become smaller. With $r_1= 1$ the trapezoidal is equal to the triangular low-pass ⇒ $h(t)= {\rm si}^2(\pi \cdot t/T)$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(5)''' Compare the <b>trapezoidal | + | '''(5)''' Compare the »<b>trapezoidal low-pass</b>« $(K_1 = 1, \ \Delta f_1 = 1, \ r_1 = 0.5)$ to the |
| − | <b>cosine-rolloff | + | »<b>cosine-rolloff low-pass</b>« $(K_2 = 1, \ \Delta f_2 = 1, \ r_2 = 0.5)$.<br> Vary $r_2$ between $0$ and $1$. Interpret the impulse response for $r_2 = 0.75$. Which low-pass satisfies the first Nyquist criterion?}} |
* With $r_1 = r_2= 0.5$ the edge drop of $H_2(f)$ is steeper by the frequency $f = 0.5$ than the edge drop of $H_1(f)$. <br> | * With $r_1 = r_2= 0.5$ the edge drop of $H_2(f)$ is steeper by the frequency $f = 0.5$ than the edge drop of $H_1(f)$. <br> | ||
| Line 224: | Line 219: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(6)''' Compare the <b>cosine-square | + | '''(6)''' Compare the »<b>cosine-square low-pass</b>« $(K_1 = 1, \ \ \Delta f_1 = 1)$ with the »<b>cosine-rolloff low-pass</b>« $(K_2 = 1, \ \ \Delta f_2 = 1,\ r_2 = 0.5)$.<br> |
Vary $r_2$ between $0$ and $1$. Interpret the results. Which low-pass satisfies the second Nyquist criterion? | Vary $r_2$ between $0$ and $1$. Interpret the results. Which low-pass satisfies the second Nyquist criterion? | ||
}} | }} | ||
| − | * $H_1(f)$ is a special case of the cosine-rolloff | + | * $H_1(f)$ is a special case of the cosine-rolloff low-pass with rolloff $r_2 =1$. The first Nyquist criterion is also fulfilled with $r_2 \ne 1$.<br> |
* According to the second Nyquist criterion $h(t)$ must also have zeros at $t=\pm 1.5$, $\pm 2.5$, $\pm 3.5$, ... $($ but not, however, at $t = \pm 0.5)$. <br> | * According to the second Nyquist criterion $h(t)$ must also have zeros at $t=\pm 1.5$, $\pm 2.5$, $\pm 3.5$, ... $($ but not, however, at $t = \pm 0.5)$. <br> | ||
| − | * For the cosine-square | + | * For the cosine-square low-pass, $h_1(t=\pm 0.5) = 0.5$ and it therefore holds $h_1(t=\pm 1) = h_1(t=\pm 1.5) = h_1(t=\pm 2)= h_1(t=\pm 2.5) = \text{...} =0$. <br> |
| − | * Only the cosine-square | + | * Only the cosine-square low-pass fulfils the first and second Nyquist criteria simultaneously: Maximum vertical and horizontal eye opening. |
| Line 274: | Line 269: | ||
==About the authors== | ==About the authors== | ||
| − | This interactive calculation tool was designed and implemented at the [https://www.ei.tum.de/en/lnt/home/ Institute for Communications Engineering] at the [https://www.tum.de/en Technical University of Munich]. | + | This interactive calculation tool was designed and implemented at the [https://www.ei.tum.de/en/lnt/home/ $\text{Institute for Communications Engineering}$] at the [https://www.tum.de/en $\text{Technical University of Munich}$]. |
| − | *The first version was created in 2005 by [[ | + | *The first version was created in 2005 by [[Biographies_and_Bibliographies/Students_involved_in_LNTwww#Ji_Li_.28Bachelorarbeit_EI_2003.2C_Diplomarbeit_EI_2005.29|»Ji Li«]] as part of her diploma thesis with “FlashMX – Actionscript” (Supervisor: [[Biographies_and_Bibliographies/LNTwww_members_from_LNT#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28at_LNT_from_1974-2024.29| »Günter Söder«]]). |
| − | *In 2017 the program was redesigned by [[ | + | |
| − | *Last revision and English version 2020 by [[ | + | *In 2017 the program was redesigned by [[Biographies_and_Bibliographies/Students_involved_in_LNTwww#David_Jobst_.28Ingenieurspraxis_Math_2017.29|»David Jobst«]] (Ingenieurspraxis_Math, Supervisor: [[Biographies_and_Bibliographies/LNTwww_members_from_LÜT#Dr.-Ing._Tasn.C3.A1d_Kernetzky_.28at_L.C3.9CT_from_2014-2022.29|»Tasnád Kernetzky«]] ) via "HTML5". |
| + | |||
| + | *Last revision and English version 2020 by [[Biographies_and_Bibliographies/Students_involved_in_LNTwww#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|»Carolin Mirschina«]] in the context of a working student activity. | ||
==Once again: Open Applet in new Tab== | ==Once again: Open Applet in new Tab== | ||
{{LntAppletLinkEnDe|frequImpResp_en|frequImpResp}} | {{LntAppletLinkEnDe|frequImpResp_en|frequImpResp}} | ||
Latest revision as of 14:39, 24 February 2025
Open Applet in new Tab Deutsche Version Öffnen
Contents
Applet Description
Real and symmetric low-pass frquency responses $H(f)$ and the corresponding impulse responses $h(t)$ are shown, namely
- Gaussian low-pass,
- rectangular low-pass,
- triangular low-pass,
- trapezoidal low-pass,
- cosine rolloff low-pass ⇒ »raised-cosine low-pass«,
- cosine rolloff squared low-pass ⇒ »cosine-square low-pass«.
It should be noted:
- The functions $H(f)$ resp. $h(t)$ are shown for up to two parameter sets in one diagram each.
- The red curves and numbers apply to the left parameter set, the blue ones to the right parameter set.
- The abscissas $t$ $($time$)$ and $f$ $($frequency$)$ as well as the ordinates $H(f)$ and $h(t)$ are normalized in each case.
- We use here the function ${\rm si}(x)=\sin(x)/x)$. The relation with the function ${\rm sinc}(x)=\sin(\pi x)/(\pi x)$ is: ${\rm sinc}(x)={\rm si}(x/\pi).$
- For the last two filters, we use in the applet the former labels "cosine rolloff low-pass" and "cosine rolloff squared low-pass".
Theoretical background
Frequency response $H(f)$ and impulse response $h(t)$
- The $\text{frequency response}$ $($or the "transfer function"$)$ $H(f)$ of a linear time-invariant transmission system gives the ratio between the output spectrum $Y(f)$ and that of the input spectrum $X(f)$:
- $$H(f) = \frac{Y(f)}{X(f)}.$$
- If the transmission behavior at low frequencies is better than at higher frequencies, it is called a »low-pass«.
- The properties of $H(f)$ are expressed in the time domain by the $\text{impulse response}$ $h(t)$. According to the $\text{second Fourier integral}$ holds:
- $$h(t)={\rm IFT} [H(f)] = \int_{-\infty}^{+\infty}H(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fourier \ transform.$$
- The inverse direction is described by the $\text{first Fourier integral}$:
- $$H(f)={\rm FT} [h(t)] = \int_{-\infty}^{+\infty}h(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} \rm FT\hspace{-0.1cm}: \ Fourier\ transform.$$
- In all examples we use real and even functions. Thus:
- $$h(t)=\int_{-\infty}^{+\infty}H(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \circ\!\!-\!\!-\! \!\!-\!\!\bullet\ \ H(f)=\int_{-\infty}^{+\infty}h(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$
- For a quadripole $[$meaning: $X(f)$ and $Y(f)$ have equal units$]$: $Y(f)$ is dimensionless.
- The unit of impulse response is $\rm 1/s$. It is true that $\rm 1/s = 1 \ Hz$, but the unit "Hertz" is unusual in this context.
- The relationship between this applet and the similarly constructed applet "Pulses and Spectra" is based on the $\text{Duality Theorem}$.
- All times are normalized to a normalization time $T$ and all frequencies are normalized to $1/T \ \Rightarrow$ the numerical values of $h(t)$ still have to be divided by $T$.
$\text{Example:}$ If one sets a rectangular low-pass with height $K_1 = 1$ and equivalent bandwidth $\Delta f_1 = 1$,
- so the frequency response $H_1(f)=1$ in the range $-1 < f < 1$ and zero outside this range.
- The impulse response $h_1(t)$ is $\rm si$–shaped with $h_1(t= 0) = 1$ and the first zero at $t=1$.
If a rectangular low-pass with $K = 1.5$ and $\Delta f = 2 \ \rm kHz$ should to be simulated, where the normalization time is $T= 1 \ \rm ms$, Then:
- The first zero is at $t=0.5\ \rm ms$ and the impulse response maximum is $h(t= 0) = 3 \cdot 10^3 \ \rm 1/s$.
Gaussian low-pass
- The Gaussian low-pass with height $K$ and $($equivalent$)$ bandwidth $\Delta f$ reads:
- $$H(f)=K\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot\hspace{0.05cm}(f/\Delta f)^2}.$$
- The equivalent bandwidth $\Delta f$ is obtained from the equal-area rectangle.
- The value at $f = \Delta f/2$ is smaller by a factor $\approx 0.456$ than the value at $f=0$.
- For the impulse response one obtains according to the inverse Fourier transform:
- $$h(t)=K\cdot \Delta f \cdot {\rm e}^{-\pi(t\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f)^2} .$$
- The smaller $\Delta f$, the wider and lower is the impulse response ⇒ $\text{Reciprocity theorem of bandwidth and impulse duration}$.
- Both $H(f)$ and $h(t)$ are not exactly equal to zero at any value of $f$ resp. $t$.
- However, for practical applications, the Gaussian pulse can be assumed to be limited in time and frequency.
- For example, $h(t)$ has already dropped to less than $0.1\% $ of its maximum at $t=1.5 \cdot \Delta t$.
Rectangular low-pass
- The rectangular low-pass with height $K$ and $($equivalent$)$ bandwidth $\Delta f$ reads:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f/2,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| = \Delta f/2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ \end{array}$$
- The $\pm \Delta f/2$ value lies midway between the left-hand and right-hand limits.
- For the impulse response $h(t)$ one obtains according to the laws of the inverse Fourier transform $($"2nd Fourier integral"$)$:
- $$h(t)=K\cdot \Delta f \cdot {\rm si}(\pi\cdot \Delta f \cdot t) \quad \text{with} \quad {\rm si}(x)={\sin(x)}/{x}.$$
- The $h(t)$ value at $t=0$ is equal to the square area of the frequency response.
- The impulse response has zeros at equidistant intervals $1/\Delta f$.
- The integral over the impulse response $h(t)$ is equal to the frequency response $H(f)$ at frequency $f=0$, thus is equal to $K$.
Triangular low-pass
- The triangular low-pass with height $K$ and $($equivalent$)$ bandwidth $\Delta f$ reads:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \Big(1-\frac{|f|}{\Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$
- The absolute physical bandwidth $B$ ⇒ [positive frequencies only] is also equal $\Delta f$, thus is as large as for the rectangular low-pass.
- For the impulse response $h(t)$ one obtains according to the second Fourier transform:
- $$h(t)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta f \cdot t) \quad \text{with} \quad {\rm si}(x)={\sin(x)}/{x}={\rm sinc}(x/\pi).$$
- $H(f)$ can be represented as a convolution of two rectangular functions $($each with width $\Delta f)$.
- It follows: $h(t)$ contains instead of the ${\rm si}$–function the ${\rm si}^2$–function.
- $h(t)$ thus also exhibits zeros at equidistant intervals $1/\Delta f$.
- The asymptotic decay of $h(t)$ occurs here with $1/t^2$, while for comparison in the case of the rectangular low-pass $h(t)$ decays with $1/t$.
Trapezoidal low-pass
- The trapezoidal low-pass with height $K$ and the two corner frequencies $f_1$ and $f_2$ reads:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{f_2-|f|}{f_2-f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$
- For the equivalent bandwidth $($equal-area rectangle$)$ the following applies: $\Delta f = f_1+f_2$.
- The rolloff factor $($in the frequency domain$)$ characterizes the slope:
- $$r=\frac{f_2-f_1}{f_2+f_1}.$$
- The special case "$r=0$" corresponds to the rectangular low-pass and the special case "$r=1$" to the triangular low-pass.
- For the impulse response, according to the inverse Fourier back transform, we obtain:
- $$h(t)=K\cdot \delta f \cdot {\rm si}(\pi\cdot \delta f \cdot t)\cdot {\rm si}(\pi \cdot r \cdot \delta f \cdot t) \quad \text{with} \quad {\rm si}(x)={\sin(x)}/{x}.$$
- The asymptotic decay of $h(t)$ lies between $1/t$ $($for rectangular low-pass or $r=0)$ and $1/t^2$ $($for triangular low-pass or $r=1)$.
Cosine rolloff low-pass
Note: In English-language literature, this filter is often also referred to as »raised-cosine low-pass«.
- The cosine-rolloff low-pass with height $K$ and the two corner frequencies $f_1$ and $f_2$ reads:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|f|-f_1}{f_2-f_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| \le f_1,} \\ {f_1\le \left| \hspace{0.05cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\left|\hspace{0.05cm} f \hspace{0.05cm} \right| \ge f_2.} \\ \end{array}$$
- For the equivalent bandwidth $($equal-area rectangle$)$ the following applies: $\Delta f = f_1+f_2$.
- The rolloff factor $($in the frequency domain$)$ characterizes the slope:
- $$r=\frac{f_2-f_1}{f_2+f_1}.$$
- The special case "$r=0$" corresponds to the rectangular low-pass and the special case "$r=1$" to the cosine-square low-pass.
- For the impulse response, according to the inverse Fourier transform, we obtain:
- $$h(t)=K\cdot \Delta f \cdot \frac{\cos(\pi \cdot r\cdot \Delta f \cdot t)}{1-(2\cdot r\cdot \Delta f \cdot t)^2} \cdot {\rm si}(\pi \cdot \Delta f \cdot t).$$
- The larger the rolloff factor $r$, the faster decreases $h(t)$ asymptotically with $t$.
Cosine rolloff squared low-pass
- This is a special case of the raised-cosine low-pass and results from it for $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}f_1=0,\ f_2= \Delta f$:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|f|\hspace{0.05cm}\cdot\hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} f\hspace{0.05cm} \right| < \Delta f,} \\ {\left| \hspace{0.05cm}f\hspace{0.05cm} \right| \ge \Delta f.} \\ \end{array}$$
- For the impulse response one obtains according to the Fourier inverse transform:
- $$h(t)=K\cdot \Delta f \cdot {\pi}/{4}\cdot \big [{\rm sinc}(\Delta f\cdot t +0.5)+{\rm sinc}(\Delta f\cdot t -0.5)\big ]\cdot {\rm sinc}(\Delta f \cdot t)\quad \text{with} \quad {\rm sinc}(x)={\sin(x)}/{(\pi x})={\rm si}(\pi x).$$
- Because of the last ${\rm sinc}$–function, $h(t)=0$ for all multiples of $T=1/\Delta f$ ⇒ The equidistant zero crossings of the cosine rolloff low-pass are preserved.
- Due to the expression in parentheses, $h(t)$ now shows further zero crossings at $t=\pm1.5 T$, $\pm2.5 T$, $\pm3.5 T$, ...
- For $t=\pm T/2$ the impulse response has the value $K\cdot \Delta f/2$.
- The asymptotic decay of $h(t)$ runs in this special case with $1/t^3$.
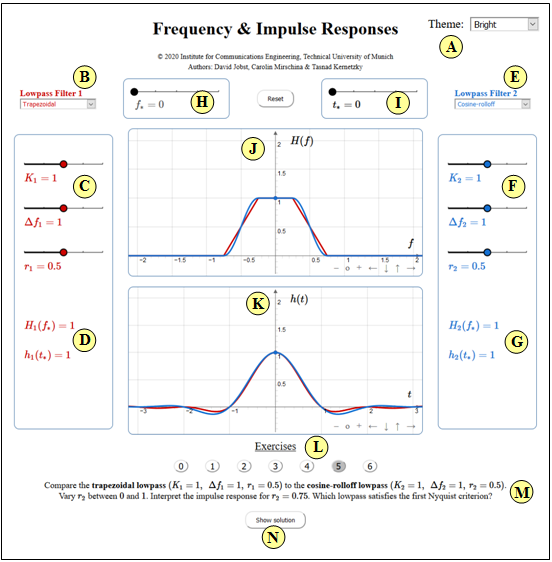
Exercises
- First select the number (1, ... , 6) of the exercise. The number 0 corresponds to a "Reset": Same setting as at the program start.
- A description of the exercise will be displayed. The parameter values are adjusted. Solution after pressing "Show solution".
- "Red" corresponds to the first parameter set ⇒ $H_1(f) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\ h_1(t)$, and "Blue" corresponds to the second parameter set ⇒ $H_2(f) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\ h_2(t)$.
- Values smaller than $0.0005$ are set to zero in the program.
(1) Compare the »red Gaussian low-pass« $(K_1 = 1, \Delta f_1 = 1)$ to the »blue rectangular low-pass« $(K_2 = 1, \Delta f_2 = 1)$. Questions:
(a) Which output signals $y(t)$ result from the signal $x(t) = 2 \cdot \cos (2\pi f_0 t -\varphi_0)$ with $f_0 = 0.5$?
(b) What are the differences between the two low-pass filters with $f_0 = 0.5 \pm f_\varepsilon$ and $f_\varepsilon \ne 0, \ f_\varepsilon \to 0$?
- (a) It holds $y(t) = A \cdot \cos (2\pi f_0 t -\varphi_0)$ with $A = 2 \cdot H(f = f_0) \ \Rightarrow \ A_1 = 0.912, \ A_2 = 1,000$. The phase $\varphi_0$ remains unchanged.
- (b) For red $ A_1 = 0.912$ is still valid. For blue it holds $A_2 = 0$ for $f_0 = 0.5000\text{...}001$ and $A_2 = 2$ for $f_0 = 0.4999\text{...}999$.
(2) Leave the settings unchanged. Which low-pass $H(f)$ fulfills the first or the second Nyquist criterion?
Here $H(f)$ denotes the total frequency response of transmitter,
channel and recettion filter.
- First Nyquist criterion: The impulse response $h(t)$ must have equidistant zero crossings at the (normalized) times $t = 1,\ 2$, ...
- The impulse response $h(t) = {\rm sinc}(\delta f \cdot t)$ of the rectangular low-pass filter fulfils this criterion with $\Delta f = 1$.
- In contrast, the first Nyquist criterion is never fulfilled for the Gaussian low-pass and there is always impulse interference.
- The second Nyquist criterion is met by neither the rectangular low-pass nor the Gaussian low-pass.
(3) Compare the »red rectangular low-pass« $(K_1 = 0.5, \Delta f_1 = 2)$ to the »blue rectangular low-pass« $(K_2 = 1, \Delta f_2 = 1)$. Then vary $\Delta f_1$ between $2$ ... $0.5$.
- With $\Delta f_1 = 2$ the zeros of $h_1(t)$ are multiples of $0.5$ ⇒ $h_1(t)$ will decay twice as fast as $h_2(t)$.
- With the present setting, $h_1(t = 0) = h_2(t = 0)$ holds, since the rectangular areas of $H_1(f)$ and $H_2(f)$ are equal.
- By decreasing $\Delta f_1$, the impulse response $h_1(t)$ becomes wider and lower. With $\Delta f_1 = 0.5$, $h_1(t)$ is twice as wide as $h_2(t)$, but simultaneously by a factor $4$ lower.
(4) Compare the »red trapezoidal low-pass« $(K_1 = 1, \ \Delta f_1 = 1, \ r_1 = 0.5)$ with »blue rectangular low-pass« $(K_2 = 1, \ \Delta f_2 = 1)$. $r_1$ varies between $0$ ... $1$.
- With $r_1 = 0.5$ the followers/precursors of $h_1(t)$ for the "trapezoid" are less than for the "rectangle" due to the flatter edge drop .
- With smaller $r_1$ followers & precursors increase. With $r_1= 0$ the trapezoidal is equal to the rectangular low-pass ⇒ $h(t)= {\rm si}(\pi \cdot t/T)$.
- With larger $r_1$ followers & precursors become smaller. With $r_1= 1$ the trapezoidal is equal to the triangular low-pass ⇒ $h(t)= {\rm si}^2(\pi \cdot t/T)$.
(5) Compare the »trapezoidal low-pass« $(K_1 = 1, \ \Delta f_1 = 1, \ r_1 = 0.5)$ to the
»cosine-rolloff low-pass« $(K_2 = 1, \ \Delta f_2 = 1, \ r_2 = 0.5)$.
Vary $r_2$ between $0$ and $1$. Interpret the impulse response for $r_2 = 0.75$. Which low-pass satisfies the first Nyquist criterion?
- With $r_1 = r_2= 0.5$ the edge drop of $H_2(f)$ is steeper by the frequency $f = 0.5$ than the edge drop of $H_1(f)$.
- With the same rolloff $r= 0.5$ the impulse response $h_2(t)$ for $t > 1$ has larger magnitudes than $h_1(t)$.
- With $r_1 = 0.5$ and $r_2 = 0.75$ $H_1(f) \approx H_2(f)$ holds and therefore also $h_1(t)
\approx h_2(t)$.
- $H_1(f)$ and $H_2(f)$ both fulfill the first Nyquist criterion: Both functions are point-symmetrical around the "Nyquist point".
- Because of $\Delta f = 1$ both $h_1(t)$ and $h_2(t)$ have zero crossings at $\pm 1$, $\pm 2$ ⇒ in each case maximum vertical eye opening.
(6) Compare the »cosine-square low-pass« $(K_1 = 1, \ \ \Delta f_1 = 1)$ with the »cosine-rolloff low-pass« $(K_2 = 1, \ \ \Delta f_2 = 1,\ r_2 = 0.5)$.
Vary $r_2$ between $0$ and $1$. Interpret the results. Which low-pass satisfies the second Nyquist criterion?
- $H_1(f)$ is a special case of the cosine-rolloff low-pass with rolloff $r_2 =1$. The first Nyquist criterion is also fulfilled with $r_2 \ne 1$.
- According to the second Nyquist criterion $h(t)$ must also have zeros at $t=\pm 1.5$, $\pm 2.5$, $\pm 3.5$, ... $($ but not, however, at $t = \pm 0.5)$.
- For the cosine-square low-pass, $h_1(t=\pm 0.5) = 0.5$ and it therefore holds $h_1(t=\pm 1) = h_1(t=\pm 1.5) = h_1(t=\pm 2)= h_1(t=\pm 2.5) = \text{...} =0$.
- Only the cosine-square low-pass fulfils the first and second Nyquist criteria simultaneously: Maximum vertical and horizontal eye opening.
Applet Manual
(A) Theme (changeable graphical user interface design)
- Dark: dark background (recommended by the authors)
- Bright: white background (recommended for beamers and printouts)
- Deuteranopia: for users with pronounced green visual impairment
- Protanopia: for users with pronounced red visual impairment
(B) Preselection for frequency response $H_1(f)$ (red curve)
(C) Parameter definition for $H_1(f)$
(D) Numeric output for $H_1(f_*)$ and $h_1(t_*)$
(E) Preselection for frequency response $H_2(f)$ (blue curve)
(F) Parameter definition for $H_2(f)$
(G) Numeric output for $H_2(f_*)$ and $h_2(t_*)$
(H) Setting the frequency $f_*$ for the numeric output
(I) Setting the time $t_*$ for the numeric output
(J) Graphic field for the frequency domain
(K) Graphic field for the time domain
(L) Selection of the exercise according to the numbers
(M) Task description and questions
(N) Show and hide sample solution
About the authors
This interactive calculation tool was designed and implemented at the $\text{Institute for Communications Engineering}$ at the $\text{Technical University of Munich}$.
- The first version was created in 2005 by »Ji Li« as part of her diploma thesis with “FlashMX – Actionscript” (Supervisor: »Günter Söder«).
- In 2017 the program was redesigned by »David Jobst« (Ingenieurspraxis_Math, Supervisor: »Tasnád Kernetzky« ) via "HTML5".
- Last revision and English version 2020 by »Carolin Mirschina« in the context of a working student activity.