Difference between revisions of "Information Theory/AWGN Channel Capacity for Continuous-Valued Input"
m (Markus verschob die Seite Informationstheorie und Quellencodierung/AWGN–Kanalkapazität bei wertkontinuierlichem Eingang nach Informationstheorie/AWGN–Kanalkapazität bei wertkontinuierlichem Eingang, ohne dabei eine Weiterleitung anzulegen) |
|||
| (68 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Information Theory for Continuous Random Variables |
|Vorherige Seite=Differentielle Entropie | |Vorherige Seite=Differentielle Entropie | ||
| − | |Nächste Seite= | + | |Nächste Seite=AWGN Channel Capacity for Discrete Input |
}} | }} | ||
| − | == | + | ==Mutual information between continuous random variables == |
| + | <br> | ||
| + | In the chapter [[Information_Theory/Application_to_Digital_Signal_Transmission#Information-theoretical_model_of_digital_signal_transmission|"Information-theoretical model of digital signal transmission"]] the "mutual information" between the two discrete random variables $X$ and $Y$ was given, among other things, in the following form: | ||
| + | |||
| + | :$$I(X;Y) = \hspace{0.5cm} \sum_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\sum_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} | ||
| + | \hspace{-0.9cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ P_{XY}(x, y)}{P_{X}(x) \cdot P_{Y}(y)} \hspace{0.05cm}.$$ | ||
| − | + | This equation simultaneously corresponds to the [[Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables#Informational_divergence_-_Kullback-Leibler_distance|"Kullback–Leibler distance"]] between the joint probability function $P_{XY}$ and the product of the two individual probability functions $P_X$ and $P_Y$: | |
| − | $$I(X;Y) = | + | :$$I(X;Y) = D(P_{XY} \hspace{0.05cm} || \hspace{0.05cm}P_{X} \cdot P_{Y}) \hspace{0.05cm}.$$ |
| − | \hspace{ | ||
| − | + | In order to derive the mutual information $I(X; Y)$ between two continuous random variables $X$ and $Y$, one proceeds as follows, whereby inverted commas indicate a quantized variable: | |
| − | + | *One quantizes the random variables $X$ and $Y$ $($with the quantization intervals ${\it Δ}x$ and ${\it Δ}y)$ and thus obtains the probability functions $P_{X\hspace{0.01cm}′}$ and $P_{Y\hspace{0.01cm}′}$. | |
| − | $$ | + | |
| + | *The "vectors" $P_{X\hspace{0.01cm}′}$ and $P_{Y\hspace{0.01cm}′}$ become infinitely long after the boundary transitions ${\it Δ}x → 0,\hspace{0.1cm} {\it Δ}y → 0$, and the joint PMF $P_{X\hspace{0.01cm}′\hspace{0.08cm}Y\hspace{0.01cm}′}$ is also infinitely extended in area. | ||
| − | + | *These boundary transitions give rise to the probability density functions of the continuous random variables according to the following equations: | |
| − | * | ||
| − | |||
| − | |||
| − | $$f_X(x_{\mu}) = \frac{P_{X'}(x_{\mu})} | + | :$$f_X(x_{\mu}) = \frac{P_{X\hspace{0.01cm}'}(x_{\mu})}{\it \Delta_x} \hspace{0.05cm}, |
| − | \hspace{0.3cm}f_Y(y_{\mu}) = \frac{P_{Y'}(y_{\mu})} | + | \hspace{0.3cm}f_Y(y_{\mu}) = \frac{P_{Y\hspace{0.01cm}'}(y_{\mu})}{\it \Delta_y} \hspace{0.05cm}, |
| − | \hspace{0.3cm}f_{XY}(x_{\mu}\hspace{0.05cm}, y_{\mu}) = \frac{P_{X'Y'}(x_{\mu}\hspace{0.05cm}, y_{\mu})}{{\it \Delta_x} \cdot {\it \Delta_y}} \hspace{0.05cm}.$$ | + | \hspace{0.3cm}f_{XY}(x_{\mu}\hspace{0.05cm}, y_{\mu}) = \frac{P_{X\hspace{0.01cm}'\hspace{0.03cm}Y\hspace{0.01cm}'}(x_{\mu}\hspace{0.05cm}, y_{\mu})} {{\it \Delta_x} \cdot {\it \Delta_y}} \hspace{0.05cm}.$$ |
| − | * | + | *The double sum in the above equation, after renaming $Δx → {\rm d}x$ and $Δy → {\rm d}y$, becomes the equation valid for continuous value random variables: |
| − | $$I(X;Y) = \hspace{0. | + | :$$I(X;Y) = \hspace{0.5cm} \int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} |
| − | \hspace{-0. | + | \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ f_{XY}(x, y) } |
{f_{X}(x) \cdot f_{Y}(y)} | {f_{X}(x) \cdot f_{Y}(y)} | ||
\hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y \hspace{0.05cm}.$$ | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y \hspace{0.05cm}.$$ | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Conclusion:}$ By splitting this double integral, it is also possible to write for the »'''mutual information'''«: | ||
| − | $$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$ | + | :$$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$ |
| − | + | The »'''joint differential entropy'''« | |
| − | $$h(XY) = -\hspace{0. | + | :$$h(XY) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} |
| − | \hspace{-0. | + | \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big[f_{XY}(x, y) \big] |
\hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$ | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$ | ||
| − | + | and the two »'''differential single entropies'''« | |
| − | $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x | + | :$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x |
\hspace{0.05cm},\hspace{0.5cm} | \hspace{0.05cm},\hspace{0.5cm} | ||
| − | h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} [f_Y(y)] \hspace{0.1cm}{\rm d}y | + | h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y |
| − | \hspace{0.05cm}.$$ | + | \hspace{0.05cm}.$$}} |
| + | |||
| + | ==On equivocation and irrelevance== | ||
| + | <br> | ||
| + | We further assume the continuous mutual information $I(X;Y) = h(X) + h(Y) - h(XY)$. This representation is also found in the following diagram $($left graph$)$. | ||
| + | |||
| + | [[File:EN_Inf_T_4_2_S2.png|right|frame|Representation of the mutual information for continuous-valued random variables]] | ||
| − | + | From this you can see that the mutual information can also be represented as follows: | |
| − | $$I(X;Y) = h(X) | + | :$$I(X;Y) = h(Y) - h(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) =h(X) - h(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}.$$ |
| − | + | These fundamental information-theoretical relationships can also be read from the graph on the right. | |
| − | [ | + | ⇒ This directional representation is particularly suitable for communication systems. The outflowing or inflowing differential entropy characterises |
| + | *the »'''equivocation'''«: | ||
| + | |||
| + | :$$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} | ||
| + | \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \big] | ||
| + | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y,$$ | ||
| − | + | *the »'''irrelevance'''«: | |
| − | $$ | + | :$$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} |
| + | \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)} \big] | ||
| + | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y.$$ | ||
| + | |||
| + | The significance of these two information-theoretic quantities will be discussed in more detail in [[Aufgaben:Exercise_4.5Z:_Again_Mutual_Information|$\text{Exercise 4.5Z}$]] . | ||
| + | |||
| + | If one compares the graphical representations of the mutual information for | ||
| + | *discrete random variables in the section [[Information_Theory/Application_to_Digital_Signal_Transmission#Information-theoretical_model_of_digital_signal_transmission|"Information-theoretical model of digital signal transmission"]], and | ||
| + | |||
| + | *continuous random variables according to the above diagram, | ||
| − | + | ||
| − | + | the only distinguishing feature is that each $($capital$)$ $H$ $($entropy; $\ge 0)$ has been replaced by a $($non-capital$)$ $h$ $($differential entropy; can be positive, negative or zero$)$. | |
| − | $ | + | *Otherwise, the mutual information is the same in both representations and $I(X; Y) ≥ 0$ always applies. |
| − | \ | + | |
| − | + | *In the following, we mostly use the "binary logarithm" ⇒ $\log_2$ and thus obtain the mutual information with the pseudo-unit "bit". | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Calculation of mutual information with additive noise == | |
| − | * | + | <br> |
| − | + | We now consider a very simple model of message transmission: | |
| + | *The random variable $X$ stands for the $($zero mean$)$ transmitted signal and is characterized by PDF $f_X(x)$ and variance $σ_X^2$. Transmission power: $P_X = σ_X^2$. | ||
| − | + | *The additive noise $N$ is given by the $($mean-free$)$ PDF $f_N(n)$ and the noise power $P_N = σ_N^2$. | |
| − | |||
| + | *If $X$ and $N$ are assumed to be statistically independent ⇒ signal-independent noise, then $\text{E}\big[X · N \big] = \text{E}\big[X \big] · \text{E}\big[N\big] = 0$ . | ||
| + | [[File:Inf_T_4_2_S3neu.png|right|frame|Transmission system with additive noise]] | ||
| − | == | + | *The received signal is $Y = X + N$. The output PDF $f_Y(y)$ can be calculated with the [[Signal_Representation/The_Convolution_Theorem_and_Operation#Convolution_in_the_time_domain|"convolution operation"]] ⇒ $f_Y(y) = f_X(x) ∗ f_N(n)$. |
| − | + | * For the received power holds: | |
| − | * | ||
| − | |||
| − | |||
| − | $$P_Y = \sigma_Y^2 = {\rm E}[Y^2] = {\rm E}[(X+N)^2] = {\rm E}[X^2] + {\rm E}[N^2] = \sigma_X^2 + \sigma_N^2 = P_X + P_N | + | :$$P_Y = \sigma_Y^2 = {\rm E}\big[Y^2\big] = {\rm E}\big[(X+N)^2\big] = {\rm E}\big[X^2\big] + {\rm E}\big[N^2\big] = \sigma_X^2 + \sigma_N^2 $$ |
| + | :$$\Rightarrow \hspace{0.3cm} P_Y = P_X + P_N | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The sketched probability density functions $($rectangular or trapezoidal$)$ are only intended to clarify the calculation process and have no practical relevance. | |
| − | [[ | + | To calculate the mutual information between input $X$ and output $Y$ there are three possibilities according to the [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang#On_equivocation_and_irrelevance|"graphic in the previous subchapter"]]: |
| + | * Calculation according to $I(X, Y) = h(X) + h(Y) - h(XY)$: | ||
| + | ::The first two terms can be calculated in a simple way from $f_X(x)$ and $f_Y(y)$ respectively. The "joint differential entropy" $h(XY)$ is problematic. For this, one needs the two-dimensional joint PDF $f_{XY}(x, y)$, which is usually not given directly. | ||
| − | + | * Calculation according to $I(X, Y) = h(Y) - h(Y|X)$: | |
| − | + | ::Here $h(Y|X)$ denotes the "differential irrelevance". It holds $h(Y|X) = h(X + N|X) = h(N)$, so that $I(X; Y)$ is very easy to calculate via the equation $f_Y(y) = f_X(x) ∗ f_N(n)$ if $f_X(x)$ and $f_N(n)$ are known. | |
| − | |||
| − | |||
| − | $h(Y|X)$ | ||
| − | $ | ||
| − | |||
| − | {{ | + | * Calculation according to $I(X, Y) = h(X) - h(X|Y)$: |
| − | + | ::According to this equation, however, one needs the "differential equivocation" $h(X|Y)$, which is more difficult to state than $h(Y|X)$. | |
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Conclusion:}$ In the following we use the middle equation and write for the »'''mutual information'''« between the input $X$ and the output $Y$ of a transmission system in the presence of additive and uncorrelated noise $N$: | ||
| − | $$I(X;Y) \hspace{-0.05cm} = \hspace{-0.01cm} h(Y) \hspace{-0.01cm}- \hspace{-0.01cm}h(N) \hspace{-0.01cm}=\hspace{-0.05cm} | + | :$$I(X;Y) \hspace{-0.05cm} = \hspace{-0.01cm} h(Y) \hspace{-0.01cm}- \hspace{-0.01cm}h(N) \hspace{-0.01cm}=\hspace{-0.05cm} |
| − | -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.65cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} [f_Y(y)] \hspace{0.1cm}{\rm d}y | + | -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.65cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y |
| − | +\hspace{-0.7cm} \int\limits_{n \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_N)} \hspace{-0.65cm} f_N(n) \cdot {\rm log} \hspace{0.1cm} [f_N(n)] \hspace{0.1cm}{\rm d}n\hspace{0.05cm}.$$ | + | +\hspace{-0.7cm} \int\limits_{n \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_N)} \hspace{-0.65cm} f_N(n) \cdot {\rm log} \hspace{0.1cm} \big[f_N(n)\big] \hspace{0.1cm}{\rm d}n\hspace{0.05cm}.$$}} |
| − | |||
| − | |||
| − | == | + | ==Channel capacity of the AWGN channel== |
| + | <br> | ||
| + | If one specifies the probability density function of the noise in the previous [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang#Calculation_of_mutual_information_with_additive_noise|"general system model"]] as Gaussian corresponding to | ||
| + | [[File:P_ID2884__Inf_T_4_2_S4_neu.png|right|frame|Derivation of the AWGN channel capacity]] | ||
| − | + | :$$f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm e}^{ | |
| − | + | - \hspace{0.05cm}{n^2}/(2 \sigma_N^2) } \hspace{0.05cm}, $$ | |
| − | $$f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm | ||
| − | - \hspace{0.05cm} | ||
| − | |||
| − | so | + | we obtain the model sketched on the right for calculating the channel capacity of the so-called [[Modulation_Methods/Quality_Criteria#Some_remarks_on_the_AWGN_channel_model|"AWGN channel"]] ⇒ "Additive White Gaussian Noise"). In the following, we usually replace the variance $\sigma_N^2$ by the power $P_N$. |
| − | [[ | + | We know from previous sections: |
| + | *The [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Definition_and_meaning_of_channel_capacity|"channel capacity"]] $C_{\rm AWGN}$ specifies the maximum mutual information $I(X; Y)$ between the input quantity $X$ and the output quantity $Y$ of the AWGN channel. | ||
| − | + | *The maximization refers to the best possible input PDF. Thus, under the [[Information_Theory/Differentielle_Entropie#Differential_entropy_of_some_power-constrained_random_variables|"power constraint"]] the following applies: | |
| − | $$ | + | :$$C_{\rm AWGN} = \max_{f_X:\hspace{0.1cm} {\rm E}[X^2 ] \le P_X} \hspace{-0.35cm} I(X;Y) |
| − | = -h(N) + \max_{f_X:\hspace{0. | + | = -h(N) + \max_{f_X:\hspace{0.1cm} {\rm E}[X^2] \le P_X} \hspace{-0.35cm} h(Y) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | *It is already taken into account that the maximization relates solely to the differential entropy $h(Y)$ ⇒ probability density function $f_Y(y)$. Indeed, for a given noise power $P_N$ ⇒ $h(N) = 1/2 · \log_2 (2π{\rm e} · P_N)$ is a constant. | ||
| + | |||
| + | *The maximum for $h(Y)$ is obtained for a Gaussian PDF $f_Y(y)$ with $P_Y = P_X + P_N$, see section [[Information_Theory/Differentielle_Entropie#Proof:_Maximum_differential_entropy_with_power_constraint|"Maximum differential entropy under power constraint"]]: | ||
| + | :$${\rm max}\big[h(Y)\big] = 1/2 · \log_2 \big[2πe · (P_X + P_N)\big].$$ | ||
| + | *However, the output PDF $f_Y(y) = f_X(x) ∗ f_N(n)$ is Gaussian only if both $f_X(x)$ and $f_N(n)$ are Gaussian functions. A striking saying about the convolution operation is: '''Gaussian remains Gaussian, and non-Gaussian never becomes (exactly) Gaussian'''. | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | [[File:P_ID2885__Inf_T_4_2_S4b_neu.png|right|frame|Numerical results for the AWGN channel capacity as a function of ${P_X}/{P_N}$]] | ||
| + | $\text{Conclusion:}$ For the AWGN channel ⇒ Gaussian noise PDF $f_N(n)$ the channel capacity results exactly when the input PDF $f_X(x)$ is also Gaussian: | ||
| − | + | :$$C_{\rm AWGN} = h_{\rm max}(Y) - h(N) = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} {P_Y}/{P_N}$$ | |
| − | + | :$$\Rightarrow \hspace{0.3cm} C_{\rm AWGN}= 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + P_X/P_N) \hspace{0.05cm}.$$}} | |
| − | |||
| − | + | ||
| − | + | ||
| − | + | ==Parallel Gaussian channels == | |
| − | $$ | + | <br> |
| − | + | [[File:EN_Inf_T_4_2_S4c.png|frame|Parallel AWGN channels]] | |
| − | + | We now consider according to the graph $K$ parallel Gaussian channels $X_1 → Y_1$, ... , $X_k → Y_k$, ... , $X_K → Y_K$. | |
| − | {{ | + | *We call the transmission powers in the $K$ channels |
| + | :$$P_1 = \text{E}[X_1^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_k = \text{E}[X_k^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_K = \text{E}[X_K^2].$$ | ||
| + | *The $K$ noise powers can also be different: | ||
| + | :$$σ_1^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_k^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_K^2.$$ | ||
| − | + | We are now looking for the maximum mutual information $I(X_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, Y_K) $ between | |
| + | *the $K$ input variables $X_1$, ... , $X_K$ and | ||
| − | + | *the $K$ output variables $Y_1$ , ... , $Y_K$, | |
| − | |||
| − | |||
| − | |||
| − | + | which we call the »'''total channel capacity'''« of this AWGN configuration. | |
| − | + | <br clear=all> | |
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Agreement:}$ | |
| − | |||
| − | $$ | + | Assume power constraint of the total AWGN system. That is: The sum of all powers $P_k$ in the $K$ individual channels must not exceed the specified value $P_X$ : |
| + | |||
| + | :$$P_1 + \hspace{0.05cm}\text{...}\hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K | ||
| + | \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Under the only slightly restrictive assumption of independent noise sources $N_1$, ... , $N_K$ it can be written for the mutual information after some intermediate steps: | |
| − | $$I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K) = h(Y_1, ... \hspace{0.05cm}, Y_K ) - \hspace{0.1cm} \sum_{k= 1}^K | + | :$$I(X_1, \hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, Y_K) = h(Y_1, ... \hspace{0.05cm}, Y_K ) - \hspace{0.1cm} \sum_{k= 1}^K |
\hspace{0.1cm} h(N_k)\hspace{0.05cm}.$$ | \hspace{0.1cm} h(N_k)\hspace{0.05cm}.$$ | ||
| − | + | *The following upper bound can be specified for this: | |
| − | $$I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K) | + | :$$I(X_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, Y_K) |
| − | \hspace{0.2cm} \le \hspace{0.1cm} \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} [h(Y_k - h(N_k)] | + | \hspace{0.2cm} \le \hspace{0.1cm} \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} \big[h(Y_k) - h(N_k)\big] |
| − | \hspace{0.2cm} \le \hspace{0.1cm} 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + | + | \hspace{0.2cm} \le \hspace{0.1cm} 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + {P_k}/{\sigma_k^2}) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | #The equal sign (identity) is valid for mean-free Gaussian input variables $X_k$ as well as for statistically independent disturbances $N_k$. | |
| − | + | #One arrives from this equation at the "maximum mutual information" ⇒ "channel capacity", if the total transmission power $P_X$ is divided as best as possible, taking into account the different noise powers in the individual channels $(σ_k^2)$. | |
| − | * | + | #This optimization problem can again be elegantly solved with the method of [https://en.wikipedia.org/wiki/Lagrange_multiplier "Lagrange multipliers"]. The following example only explains the result. |
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
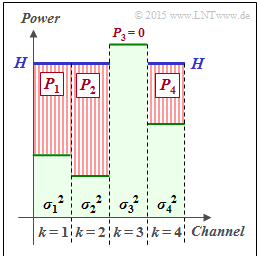
| + | [[File:EN_Inf_T_4_2_S4d_v2.png|right|frame|Best possible power allocation for $K = 4$ $($"Water–Filling"$)$]] | ||
| + | $\text{Example 1:}$ We consider $K = 4$ parallel Gaussian channels with four different noise powers $σ_1^2$, ... , $σ_4^2$ according to the adjacent figure (faint green background). | ||
| + | *The best possible allocation of the transmission power among the four channels is sought. | ||
| + | |||
| + | *If one were to slowly fill this profile with water, the water would initially flow only into $\text{channel 2}$. | ||
| + | |||
| + | *If you continue to pour, some water will also accumulate in $\text{channel 1}$ and later also in $\text{channel 4}$. | ||
| − | + | The drawn "water level" $H$ describes exactly the point in time when the sum $P_1 + P_2 + P_4$ corresponds to the total available transmssion power $P_X$ : | |
| + | *The optimal power allocation for this example results in $P_2 > P_1 > P_4$ as well as $P_3 = 0$. | ||
| − | + | *Only with a larger transmission power $P_X$, a small power $P_3$ would also be allocated to the third channel. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | This allocation procedure is called a »'''Water–Filling algorithm'''«.}} | ||
| − | |||
| − | [[File: | + | {{GraueBox|TEXT= |
| − | + | $\text{Example 2:}$ | |
| − | $$C_{\rm | + | If all $K$ Gaussian channels are equally disturbed ⇒ $σ_1^2 = \hspace{0.15cm}\text{...}\hspace{0.15cm} = σ_K^2 = P_N$, one should naturally allocate the total available transmission power $P_X$ equally to all channels: $P_k = P_X/K$. For the total capacity we then obtain: |
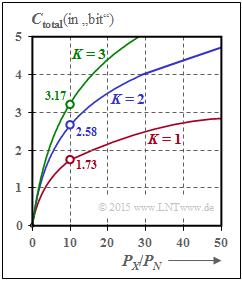
| + | [[File:EN_Inf_Z_4_1.png|right|frame|Capacity for $K$ parallel channels]] | ||
| + | :$$C_{\rm total} | ||
= \frac{ K}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{K \cdot P_N}) | = \frac{ K}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{K \cdot P_N}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The graph shows the total capacity as a function of $P_X/P_N$ for $K = 1$, $K = 2$ and $K = 3$: | |
| − | * | + | *With $P_X/P_N = 10 \ ⇒ \ 10 · \text{lg} (P_X/P_N) = 10 \ \text{dB}$ and $K = 2$, the total capacitance becomes approximately $50\%$ larger if the total power $P_X$ is divided equally between two channels: $P_1 = P_2 = P_X/2$. |
| − | * | + | |
| + | *In the borderline case $P_X/P_N → ∞$, the total capacity increases by a factor $K$ ⇒ doubling at $K = 2$. | ||
| + | |||
| + | |||
| + | The two identical and independent channels can be realized in different ways, for example by multiplexing in time, frequency or space. | ||
| + | |||
| + | However, the case $K = 2$ can also be realized by using orthogonal basis functions such as "cosine" and "sine" as for example with | ||
| + | |||
| + | * [[Modulation_Methods/Quadratur–Amplitudenmodulation|"quadrature amplitude modulation"]] $\rm (QAM)$ or | ||
| + | |||
| + | * [[Modulation_Methods/Quadrature_Amplitude_Modulation#Other_signal_space_constellations|"multi-level phase modulation"]] such as $\rm QPSK$ or $\rm 8–PSK$.}} | ||
| + | |||
| + | ==Exercises for the chapter == | ||
| + | <br> | ||
| + | [[Aufgaben:Exercise_4.5:_Mutual_Information_from_2D-PDF|Exercise 4.5: Mutual Information from 2D-PDF]] | ||
| + | |||
| + | [[Aufgaben:Exercise_4.5Z:_Again_Mutual_Information|Exercise 4.5Z: Again Mutual Information]] | ||
| − | + | [[Aufgaben:Exercise_4.6:_AWGN_Channel_Capacity|Exercise 4.6: AWGN Channel Capacity]] | |
| − | |||
| − | + | [[Aufgaben:Exercise_4.7:_Several_Parallel_Gaussian_Channels|Exercise 4.7: Several Parallel Gaussian Channels]] | |
| + | [[Aufgaben:Exercise_4.7Z:_About_the_Water_Filling_Algorithm|Exercise 4.7Z: About the Water Filling Algorithm]] | ||
{{Display}} | {{Display}} | ||
Latest revision as of 15:22, 28 February 2023
Contents
Mutual information between continuous random variables
In the chapter "Information-theoretical model of digital signal transmission" the "mutual information" between the two discrete random variables $X$ and $Y$ was given, among other things, in the following form:
- $$I(X;Y) = \hspace{0.5cm} \sum_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\sum_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} \hspace{-0.9cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ P_{XY}(x, y)}{P_{X}(x) \cdot P_{Y}(y)} \hspace{0.05cm}.$$
This equation simultaneously corresponds to the "Kullback–Leibler distance" between the joint probability function $P_{XY}$ and the product of the two individual probability functions $P_X$ and $P_Y$:
- $$I(X;Y) = D(P_{XY} \hspace{0.05cm} || \hspace{0.05cm}P_{X} \cdot P_{Y}) \hspace{0.05cm}.$$
In order to derive the mutual information $I(X; Y)$ between two continuous random variables $X$ and $Y$, one proceeds as follows, whereby inverted commas indicate a quantized variable:
- One quantizes the random variables $X$ and $Y$ $($with the quantization intervals ${\it Δ}x$ and ${\it Δ}y)$ and thus obtains the probability functions $P_{X\hspace{0.01cm}′}$ and $P_{Y\hspace{0.01cm}′}$.
- The "vectors" $P_{X\hspace{0.01cm}′}$ and $P_{Y\hspace{0.01cm}′}$ become infinitely long after the boundary transitions ${\it Δ}x → 0,\hspace{0.1cm} {\it Δ}y → 0$, and the joint PMF $P_{X\hspace{0.01cm}′\hspace{0.08cm}Y\hspace{0.01cm}′}$ is also infinitely extended in area.
- These boundary transitions give rise to the probability density functions of the continuous random variables according to the following equations:
- $$f_X(x_{\mu}) = \frac{P_{X\hspace{0.01cm}'}(x_{\mu})}{\it \Delta_x} \hspace{0.05cm}, \hspace{0.3cm}f_Y(y_{\mu}) = \frac{P_{Y\hspace{0.01cm}'}(y_{\mu})}{\it \Delta_y} \hspace{0.05cm}, \hspace{0.3cm}f_{XY}(x_{\mu}\hspace{0.05cm}, y_{\mu}) = \frac{P_{X\hspace{0.01cm}'\hspace{0.03cm}Y\hspace{0.01cm}'}(x_{\mu}\hspace{0.05cm}, y_{\mu})} {{\it \Delta_x} \cdot {\it \Delta_y}} \hspace{0.05cm}.$$
- The double sum in the above equation, after renaming $Δx → {\rm d}x$ and $Δy → {\rm d}y$, becomes the equation valid for continuous value random variables:
- $$I(X;Y) = \hspace{0.5cm} \int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ f_{XY}(x, y) } {f_{X}(x) \cdot f_{Y}(y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y \hspace{0.05cm}.$$
$\text{Conclusion:}$ By splitting this double integral, it is also possible to write for the »mutual information«:
- $$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$
The »joint differential entropy«
- $$h(XY) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big[f_{XY}(x, y) \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$
and the two »differential single entropies«
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},\hspace{0.5cm} h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$
On equivocation and irrelevance
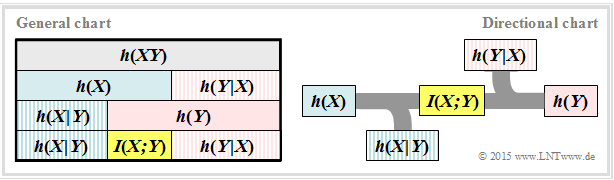
We further assume the continuous mutual information $I(X;Y) = h(X) + h(Y) - h(XY)$. This representation is also found in the following diagram $($left graph$)$.
From this you can see that the mutual information can also be represented as follows:
- $$I(X;Y) = h(Y) - h(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) =h(X) - h(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}.$$
These fundamental information-theoretical relationships can also be read from the graph on the right.
⇒ This directional representation is particularly suitable for communication systems. The outflowing or inflowing differential entropy characterises
- the »equivocation«:
- $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y,$$
- the »irrelevance«:
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = - \hspace{-0.3cm}\int\limits_{\hspace{-0.9cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{Y}\hspace{-0.08cm})} \hspace{-1.1cm}\int\limits_{\hspace{1.3cm} x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{X}\hspace{-0.08cm})} \hspace{-0.9cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \hspace{0.1cm} \big [{f_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)} \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y.$$
The significance of these two information-theoretic quantities will be discussed in more detail in $\text{Exercise 4.5Z}$ .
If one compares the graphical representations of the mutual information for
- discrete random variables in the section "Information-theoretical model of digital signal transmission", and
- continuous random variables according to the above diagram,
the only distinguishing feature is that each $($capital$)$ $H$ $($entropy; $\ge 0)$ has been replaced by a $($non-capital$)$ $h$ $($differential entropy; can be positive, negative or zero$)$.
- Otherwise, the mutual information is the same in both representations and $I(X; Y) ≥ 0$ always applies.
- In the following, we mostly use the "binary logarithm" ⇒ $\log_2$ and thus obtain the mutual information with the pseudo-unit "bit".
Calculation of mutual information with additive noise
We now consider a very simple model of message transmission:
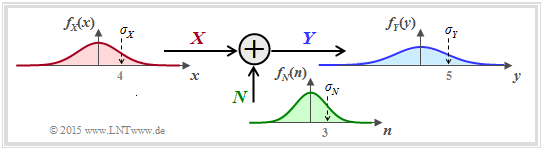
- The random variable $X$ stands for the $($zero mean$)$ transmitted signal and is characterized by PDF $f_X(x)$ and variance $σ_X^2$. Transmission power: $P_X = σ_X^2$.
- The additive noise $N$ is given by the $($mean-free$)$ PDF $f_N(n)$ and the noise power $P_N = σ_N^2$.
- If $X$ and $N$ are assumed to be statistically independent ⇒ signal-independent noise, then $\text{E}\big[X · N \big] = \text{E}\big[X \big] · \text{E}\big[N\big] = 0$ .
- The received signal is $Y = X + N$. The output PDF $f_Y(y)$ can be calculated with the "convolution operation" ⇒ $f_Y(y) = f_X(x) ∗ f_N(n)$.
- For the received power holds:
- $$P_Y = \sigma_Y^2 = {\rm E}\big[Y^2\big] = {\rm E}\big[(X+N)^2\big] = {\rm E}\big[X^2\big] + {\rm E}\big[N^2\big] = \sigma_X^2 + \sigma_N^2 $$
- $$\Rightarrow \hspace{0.3cm} P_Y = P_X + P_N \hspace{0.05cm}.$$
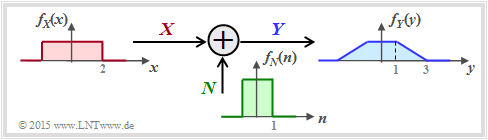
The sketched probability density functions $($rectangular or trapezoidal$)$ are only intended to clarify the calculation process and have no practical relevance.
To calculate the mutual information between input $X$ and output $Y$ there are three possibilities according to the "graphic in the previous subchapter":
- Calculation according to $I(X, Y) = h(X) + h(Y) - h(XY)$:
- The first two terms can be calculated in a simple way from $f_X(x)$ and $f_Y(y)$ respectively. The "joint differential entropy" $h(XY)$ is problematic. For this, one needs the two-dimensional joint PDF $f_{XY}(x, y)$, which is usually not given directly.
- Calculation according to $I(X, Y) = h(Y) - h(Y|X)$:
- Here $h(Y|X)$ denotes the "differential irrelevance". It holds $h(Y|X) = h(X + N|X) = h(N)$, so that $I(X; Y)$ is very easy to calculate via the equation $f_Y(y) = f_X(x) ∗ f_N(n)$ if $f_X(x)$ and $f_N(n)$ are known.
- Calculation according to $I(X, Y) = h(X) - h(X|Y)$:
- According to this equation, however, one needs the "differential equivocation" $h(X|Y)$, which is more difficult to state than $h(Y|X)$.
$\text{Conclusion:}$ In the following we use the middle equation and write for the »mutual information« between the input $X$ and the output $Y$ of a transmission system in the presence of additive and uncorrelated noise $N$:
- $$I(X;Y) \hspace{-0.05cm} = \hspace{-0.01cm} h(Y) \hspace{-0.01cm}- \hspace{-0.01cm}h(N) \hspace{-0.01cm}=\hspace{-0.05cm} -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.65cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y +\hspace{-0.7cm} \int\limits_{n \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_N)} \hspace{-0.65cm} f_N(n) \cdot {\rm log} \hspace{0.1cm} \big[f_N(n)\big] \hspace{0.1cm}{\rm d}n\hspace{0.05cm}.$$
Channel capacity of the AWGN channel
If one specifies the probability density function of the noise in the previous "general system model" as Gaussian corresponding to
- $$f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{n^2}/(2 \sigma_N^2) } \hspace{0.05cm}, $$
we obtain the model sketched on the right for calculating the channel capacity of the so-called "AWGN channel" ⇒ "Additive White Gaussian Noise"). In the following, we usually replace the variance $\sigma_N^2$ by the power $P_N$.
We know from previous sections:
- The "channel capacity" $C_{\rm AWGN}$ specifies the maximum mutual information $I(X; Y)$ between the input quantity $X$ and the output quantity $Y$ of the AWGN channel.
- The maximization refers to the best possible input PDF. Thus, under the "power constraint" the following applies:
- $$C_{\rm AWGN} = \max_{f_X:\hspace{0.1cm} {\rm E}[X^2 ] \le P_X} \hspace{-0.35cm} I(X;Y) = -h(N) + \max_{f_X:\hspace{0.1cm} {\rm E}[X^2] \le P_X} \hspace{-0.35cm} h(Y) \hspace{0.05cm}.$$
- It is already taken into account that the maximization relates solely to the differential entropy $h(Y)$ ⇒ probability density function $f_Y(y)$. Indeed, for a given noise power $P_N$ ⇒ $h(N) = 1/2 · \log_2 (2π{\rm e} · P_N)$ is a constant.
- The maximum for $h(Y)$ is obtained for a Gaussian PDF $f_Y(y)$ with $P_Y = P_X + P_N$, see section "Maximum differential entropy under power constraint":
- $${\rm max}\big[h(Y)\big] = 1/2 · \log_2 \big[2πe · (P_X + P_N)\big].$$
- However, the output PDF $f_Y(y) = f_X(x) ∗ f_N(n)$ is Gaussian only if both $f_X(x)$ and $f_N(n)$ are Gaussian functions. A striking saying about the convolution operation is: Gaussian remains Gaussian, and non-Gaussian never becomes (exactly) Gaussian.
$\text{Conclusion:}$ For the AWGN channel ⇒ Gaussian noise PDF $f_N(n)$ the channel capacity results exactly when the input PDF $f_X(x)$ is also Gaussian:
- $$C_{\rm AWGN} = h_{\rm max}(Y) - h(N) = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} {P_Y}/{P_N}$$
- $$\Rightarrow \hspace{0.3cm} C_{\rm AWGN}= 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + P_X/P_N) \hspace{0.05cm}.$$
Parallel Gaussian channels
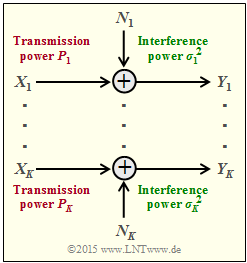
We now consider according to the graph $K$ parallel Gaussian channels $X_1 → Y_1$, ... , $X_k → Y_k$, ... , $X_K → Y_K$.
- We call the transmission powers in the $K$ channels
- $$P_1 = \text{E}[X_1^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_k = \text{E}[X_k^2], \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ P_K = \text{E}[X_K^2].$$
- The $K$ noise powers can also be different:
- $$σ_1^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_k^2, \hspace{0.15cm}\text{...}\hspace{0.15cm} ,\ σ_K^2.$$
We are now looking for the maximum mutual information $I(X_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.15cm}\text{...}\hspace{0.15cm}, Y_K) $ between
- the $K$ input variables $X_1$, ... , $X_K$ and
- the $K$ output variables $Y_1$ , ... , $Y_K$,
which we call the »total channel capacity« of this AWGN configuration.
$\text{Agreement:}$
Assume power constraint of the total AWGN system. That is: The sum of all powers $P_k$ in the $K$ individual channels must not exceed the specified value $P_X$ :
- $$P_1 + \hspace{0.05cm}\text{...}\hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$
Under the only slightly restrictive assumption of independent noise sources $N_1$, ... , $N_K$ it can be written for the mutual information after some intermediate steps:
- $$I(X_1, \hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, Y_K) = h(Y_1, ... \hspace{0.05cm}, Y_K ) - \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} h(N_k)\hspace{0.05cm}.$$
- The following upper bound can be specified for this:
- $$I(X_1,\hspace{0.05cm}\text{...}\hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, Y_K) \hspace{0.2cm} \le \hspace{0.1cm} \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} \big[h(Y_k) - h(N_k)\big] \hspace{0.2cm} \le \hspace{0.1cm} 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + {P_k}/{\sigma_k^2}) \hspace{0.05cm}.$$
- The equal sign (identity) is valid for mean-free Gaussian input variables $X_k$ as well as for statistically independent disturbances $N_k$.
- One arrives from this equation at the "maximum mutual information" ⇒ "channel capacity", if the total transmission power $P_X$ is divided as best as possible, taking into account the different noise powers in the individual channels $(σ_k^2)$.
- This optimization problem can again be elegantly solved with the method of "Lagrange multipliers". The following example only explains the result.
$\text{Example 1:}$ We consider $K = 4$ parallel Gaussian channels with four different noise powers $σ_1^2$, ... , $σ_4^2$ according to the adjacent figure (faint green background).
- The best possible allocation of the transmission power among the four channels is sought.
- If one were to slowly fill this profile with water, the water would initially flow only into $\text{channel 2}$.
- If you continue to pour, some water will also accumulate in $\text{channel 1}$ and later also in $\text{channel 4}$.
The drawn "water level" $H$ describes exactly the point in time when the sum $P_1 + P_2 + P_4$ corresponds to the total available transmssion power $P_X$ :
- The optimal power allocation for this example results in $P_2 > P_1 > P_4$ as well as $P_3 = 0$.
- Only with a larger transmission power $P_X$, a small power $P_3$ would also be allocated to the third channel.
This allocation procedure is called a »Water–Filling algorithm«.
$\text{Example 2:}$ If all $K$ Gaussian channels are equally disturbed ⇒ $σ_1^2 = \hspace{0.15cm}\text{...}\hspace{0.15cm} = σ_K^2 = P_N$, one should naturally allocate the total available transmission power $P_X$ equally to all channels: $P_k = P_X/K$. For the total capacity we then obtain:
- $$C_{\rm total} = \frac{ K}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{K \cdot P_N}) \hspace{0.05cm}.$$
The graph shows the total capacity as a function of $P_X/P_N$ for $K = 1$, $K = 2$ and $K = 3$:
- With $P_X/P_N = 10 \ ⇒ \ 10 · \text{lg} (P_X/P_N) = 10 \ \text{dB}$ and $K = 2$, the total capacitance becomes approximately $50\%$ larger if the total power $P_X$ is divided equally between two channels: $P_1 = P_2 = P_X/2$.
- In the borderline case $P_X/P_N → ∞$, the total capacity increases by a factor $K$ ⇒ doubling at $K = 2$.
The two identical and independent channels can be realized in different ways, for example by multiplexing in time, frequency or space.
However, the case $K = 2$ can also be realized by using orthogonal basis functions such as "cosine" and "sine" as for example with
- "quadrature amplitude modulation" $\rm (QAM)$ or
- "multi-level phase modulation" such as $\rm QPSK$ or $\rm 8–PSK$.
Exercises for the chapter
Exercise 4.5: Mutual Information from 2D-PDF
Exercise 4.5Z: Again Mutual Information
Exercise 4.6: AWGN Channel Capacity
Exercise 4.7: Several Parallel Gaussian Channels
Exercise 4.7Z: About the Water Filling Algorithm