Difference between revisions of "Aufgaben:Exercise 1.2: Entropy of Ternary Sources"
m (Text replacement - "autocorrelation" to "auto-correlation") |
|||
| (26 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Discrete_Memoryless_Sources}} |
| − | }} | ||
| − | [[File: | + | [[File:Inf_A_1_2_vers2.png|right|frame|Probabilities of two ternary sources]] |
| − | + | The entropy of a discrete memoryless source with $M$ possible symbols is: | |
:$$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} | :$$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} | ||
| − | {\rm | + | {\rm pseudo unit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$ |
| − | + | Here, the $p_\mu$ denote the occurrence probabilities of the individual symbols or events. In the present example, the events are denoted by $\rm R$(ed), $\rm G$(reen) and $\rm S$(chwarz) with "Schwarz" being the German word for "Black". | |
| − | + | *For a binary source with the occurrence probabilities $p$ and $1-p$ this can be written: | |
:$$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot | :$$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot | ||
| − | {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm}.$$ | + | {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm},\hspace{0.3cm} |
| − | + | \text{pseudo–unit: bit}\hspace{0.05cm}.$$ | |
| + | *The entropy of a multilevel source can often be expressed with this "binary entropy function" $H_{\rm bin}(p)$. | ||
| + | |||
| − | + | In this task, two ternary sources with the symbol probabilities according to the above graph are considered: | |
| − | + | # source $\rm Q_1$ with $p_{\rm G }= 1/2$, $p_{\rm S }= 1/3$ and $p_{\rm R }= 1/6$, | |
| + | # source $\rm Q_2$ with $p_{\rm G }= p$ and $p_{\rm S } = p_{\rm R } = (1-p)/2$. | ||
| − | |||
| − | + | *The ternary source $\rm Q_2$ can also be applied to "Roulette" when a player bets only on the squares $\rm R$(ed), $\rm S$(chwarz) and $\rm G$(reen) (the "zero"). This type of game is referred to as $\text{Roulette 1}$ in the question section. | |
| − | + | *In contrast, $\text{Roulette 2}$ indicates that the player bets on single numbers $(0$, ... , $36)$. | |
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | ''Hint:'' | ||
| + | *The task belongs to the chapter [[Information_Theory/Gedächtnislose_Nachrichtenquellen|Discrete Memoryless Sources]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the entropy $H$ of the source $\rm \underline{Q_1}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H \ = \ $ { 1.46 3% } $\ \rm bit$ |
| − | { | + | {Which of the following statements are true if $\rm R$, $\rm G$ and $\rm S$ are represented by the numerical values $-1$, $0$ and $+1$ ? |
| − | |type=" | + | |type="()"} |
| − | - | + | - The result is a smaller entropy. |
| − | + | + | + The entropy remains the same. |
| − | - | + | - The result is a greater entropy. |
| − | { | + | {Determine the entropy of the source $\rm \underline{Q_2}$ using the binary entropy function $H_{\rm bin}(p)$. What value results for $\underline{p = 0.5}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H \ = \ $ { 1.5 3% } $\ \rm bit$ |
| − | { | + | {For which $p$–value of the source $\rm \underline{Q_2}$ does the maximum entropy result: $H → H_\text{max}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $p \ = \ $ { 0.333 3% } |
| − | { | + | {What is the entropy of the source model $\text{Roulette 1}$, i.e. with respect to the events $\rm R$(ed), $\rm S$(chwarz) and $\rm G$(reen) (the "zero")? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H \ = \ $ { 1.152 3% } $\ \rm bit$ |
| − | { | + | {What is the entropy of $\text{Roulette 2}$ , i.e. with regard to the numbers $0$, ... , $36$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $H \ = \ $ { 5.209 3% } $\ \rm bit$ |
| Line 65: | Line 74: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' With the "symbol" probabilities $1/2$, $1/3$ and $1/6$ we get the following entropy value: | |
| − | :$$H \hspace{0.1cm} = \hspace{0.1cm} 1/2 \cdot {\rm log}_2\hspace{0.1cm}(2) +1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) +1/6 \cdot {\rm log}_2\hspace{0.1cm}(6) = | + | :$$H \hspace{0.1cm} = \hspace{0.1cm} 1/2 \cdot {\rm log}_2\hspace{0.1cm}(2) +1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) +1/6 \cdot {\rm log}_2\hspace{0.1cm}(6) =(1/2 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(2) + (1/3 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(3) \hspace{0.15cm}\underline {\approx 1.46 \, {\rm bit}} \hspace{0.05cm}.$$ |
| − | + | ||
| − | + | ||
| − | + | ||
| + | '''(2)''' <u>Proposed solution 2</u> is correct: | ||
| + | *The entropy depends only on the probabilities of occurrence. | ||
| + | *It does not matter which numerical values or physical quantities one assigns to the individual symbols. | ||
| + | *It is different with mean values or the ACF (auto correlation function) calculation. If only symbols are given, no moments can be calculated for them. | ||
| + | *Moreover, the mean values, auto-correlation, etc. depend on whether one agrees on the assignment bipolar $(-1, \hspace{0.10cm}0, \hspace{0.05cm}+1)$ or unipolar $(0, \hspace{0.05cm}1, \hspace{0.05cm}2)$ . | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The entropy of source $\rm Q_2$ can be expressed as follows: | ||
| + | :$$H \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ 2 \cdot \frac{1-p}{2} \cdot {\rm log}_2\hspace{0.1cm}\frac {2}{1-p}= p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{1-p} + (1-p)\cdot {\rm log}_2\hspace{0.1cm}(2)= H_{\rm bin}(p) + 1-p \hspace{0.05cm}.$$ | ||
| + | *For $p = 0.5$ ⇒ $H_{\rm bin}(p) = 1$ , we get $\underline{H = 1.5\hspace{0.05cm}\rm bit}$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' The maximum entropy of a memoryless source with symbol set size $M$ is obtained when all $M$ symbols are equally probable. | |
| + | *For the special case $M=3$ it follows: | ||
:$$p_{\rm R} + p_{\rm G} + p_{\rm S} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | :$$p_{\rm R} + p_{\rm G} + p_{\rm S} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| − | \underline {p = 1/3}\hspace{0.05cm}.$$ | + | \underline {p = 1/3 \approx 0.333}\hspace{0.05cm}.$$ |
| − | + | *Thus, using the result of sub-task '''(3)''' , we obtain the following entropy: | |
| − | :$$H | + | :$$H = H_{\rm bin}(1/3) + 1-1/3 = 1/3 \cdot |
| − | {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3/2) + 2/3 | + | {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3/2) + 2/3 $$ |
| − | + | :$$\Rightarrow \hspace{0.3cm}H = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot | |
{\rm log}_2\hspace{0.1cm}(3) - 2/3 \cdot {\rm log}_2\hspace{0.1cm}(2)+ 2/3 = | {\rm log}_2\hspace{0.1cm}(3) - 2/3 \cdot {\rm log}_2\hspace{0.1cm}(2)+ 2/3 = | ||
{\rm log}_2\hspace{0.1cm}(3) = {1.585 \, {\rm bit}} | {\rm log}_2\hspace{0.1cm}(3) = {1.585 \, {\rm bit}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| + | |||
| + | '''(5)''' The source model $\text{Roulette 1}$ is information theoretically equal to the configuration $\rm Q_2$ with $p = 1/37$: | ||
:$$p_{\rm G} = p = \frac{1}{37}\hspace{0.05cm},\hspace{0.2cm} p_{\rm R} = p_{\rm S} = \frac{1-p}{2} = \frac{18}{37} \hspace{0.05cm}.$$ | :$$p_{\rm G} = p = \frac{1}{37}\hspace{0.05cm},\hspace{0.2cm} p_{\rm R} = p_{\rm S} = \frac{1-p}{2} = \frac{18}{37} \hspace{0.05cm}.$$ | ||
| − | + | *Thus, using the result of subtask '''(3)''', we obtain: | |
| − | :$$H | + | :$$H = H_{\rm bin}(1/37) + \frac{36}{37} = \frac{1}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) - \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}36 + \frac{36}{37} = |
| − | + | {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot ( 1- {\rm log}_2\hspace{0.1cm}(36)) = 5.209 - 4.057 \hspace{0.15cm} \underline { = 1.152 \, {\rm bit}} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| + | |||
| + | '''(6)''' If we bet on single numbers in roulette ⇒ source model $\text{Roulette 2}$, all numbers from $0$ to $36$ are equally probable and we get: | ||
:$$H = {\rm log}_2\hspace{0.1cm}(37) \hspace{0.15cm} \underline { = 5.209 \, {\rm bit}} | :$$H = {\rm log}_2\hspace{0.1cm}(37) \hspace{0.15cm} \underline { = 5.209 \, {\rm bit}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 105: | Line 125: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^1.1 Memoryless Sources^]] |
Latest revision as of 12:29, 17 February 2022
The entropy of a discrete memoryless source with $M$ possible symbols is:
- $$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} {\rm pseudo unit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$
Here, the $p_\mu$ denote the occurrence probabilities of the individual symbols or events. In the present example, the events are denoted by $\rm R$(ed), $\rm G$(reen) and $\rm S$(chwarz) with "Schwarz" being the German word for "Black".
- For a binary source with the occurrence probabilities $p$ and $1-p$ this can be written:
- $$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm},\hspace{0.3cm} \text{pseudo–unit: bit}\hspace{0.05cm}.$$
- The entropy of a multilevel source can often be expressed with this "binary entropy function" $H_{\rm bin}(p)$.
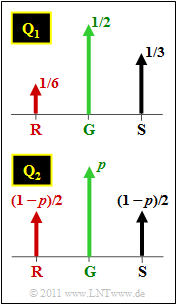
In this task, two ternary sources with the symbol probabilities according to the above graph are considered:
- source $\rm Q_1$ with $p_{\rm G }= 1/2$, $p_{\rm S }= 1/3$ and $p_{\rm R }= 1/6$,
- source $\rm Q_2$ with $p_{\rm G }= p$ and $p_{\rm S } = p_{\rm R } = (1-p)/2$.
- The ternary source $\rm Q_2$ can also be applied to "Roulette" when a player bets only on the squares $\rm R$(ed), $\rm S$(chwarz) and $\rm G$(reen) (the "zero"). This type of game is referred to as $\text{Roulette 1}$ in the question section.
- In contrast, $\text{Roulette 2}$ indicates that the player bets on single numbers $(0$, ... , $36)$.
Hint:
- The task belongs to the chapter Discrete Memoryless Sources.
Questions
Solution
- $$H \hspace{0.1cm} = \hspace{0.1cm} 1/2 \cdot {\rm log}_2\hspace{0.1cm}(2) +1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) +1/6 \cdot {\rm log}_2\hspace{0.1cm}(6) =(1/2 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(2) + (1/3 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(3) \hspace{0.15cm}\underline {\approx 1.46 \, {\rm bit}} \hspace{0.05cm}.$$
(2) Proposed solution 2 is correct:
- The entropy depends only on the probabilities of occurrence.
- It does not matter which numerical values or physical quantities one assigns to the individual symbols.
- It is different with mean values or the ACF (auto correlation function) calculation. If only symbols are given, no moments can be calculated for them.
- Moreover, the mean values, auto-correlation, etc. depend on whether one agrees on the assignment bipolar $(-1, \hspace{0.10cm}0, \hspace{0.05cm}+1)$ or unipolar $(0, \hspace{0.05cm}1, \hspace{0.05cm}2)$ .
(3) The entropy of source $\rm Q_2$ can be expressed as follows:
- $$H \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ 2 \cdot \frac{1-p}{2} \cdot {\rm log}_2\hspace{0.1cm}\frac {2}{1-p}= p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{1-p} + (1-p)\cdot {\rm log}_2\hspace{0.1cm}(2)= H_{\rm bin}(p) + 1-p \hspace{0.05cm}.$$
- For $p = 0.5$ ⇒ $H_{\rm bin}(p) = 1$ , we get $\underline{H = 1.5\hspace{0.05cm}\rm bit}$.
(4) The maximum entropy of a memoryless source with symbol set size $M$ is obtained when all $M$ symbols are equally probable.
- For the special case $M=3$ it follows:
- $$p_{\rm R} + p_{\rm G} + p_{\rm S} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {p = 1/3 \approx 0.333}\hspace{0.05cm}.$$
- Thus, using the result of sub-task (3) , we obtain the following entropy:
- $$H = H_{\rm bin}(1/3) + 1-1/3 = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3/2) + 2/3 $$
- $$\Rightarrow \hspace{0.3cm}H = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3) - 2/3 \cdot {\rm log}_2\hspace{0.1cm}(2)+ 2/3 = {\rm log}_2\hspace{0.1cm}(3) = {1.585 \, {\rm bit}} \hspace{0.05cm}.$$
(5) The source model $\text{Roulette 1}$ is information theoretically equal to the configuration $\rm Q_2$ with $p = 1/37$:
- $$p_{\rm G} = p = \frac{1}{37}\hspace{0.05cm},\hspace{0.2cm} p_{\rm R} = p_{\rm S} = \frac{1-p}{2} = \frac{18}{37} \hspace{0.05cm}.$$
- Thus, using the result of subtask (3), we obtain:
- $$H = H_{\rm bin}(1/37) + \frac{36}{37} = \frac{1}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) - \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}36 + \frac{36}{37} = {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot ( 1- {\rm log}_2\hspace{0.1cm}(36)) = 5.209 - 4.057 \hspace{0.15cm} \underline { = 1.152 \, {\rm bit}} \hspace{0.05cm}.$$
(6) If we bet on single numbers in roulette ⇒ source model $\text{Roulette 2}$, all numbers from $0$ to $36$ are equally probable and we get:
- $$H = {\rm log}_2\hspace{0.1cm}(37) \hspace{0.15cm} \underline { = 5.209 \, {\rm bit}} \hspace{0.05cm}.$$