Difference between revisions of "Aufgaben:Exercise 2.5: Residual Redundancy with LZW Coding"
| (36 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Compression_According_to_Lempel,_Ziv_and_Welch |
}} | }} | ||
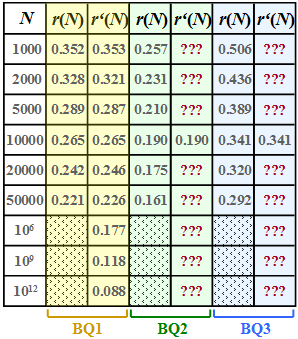
| − | [[File:P_ID2446__Inf_A_2_5_neu.png|right|]] | + | [[File:P_ID2446__Inf_A_2_5_neu.png|right|frame|Residual redundancy $r(N)$ and approximation $r\hspace{0.05cm}'(N)$ of three sources]] |
| − | : | + | We assume here a binary input sequence of length $N$ and consider three different binary sources: |
| + | * $\rm BQ1$: Symbol probabilities $p_{\rm A} = 0.89$ and $p_{\rm B} = 0.11$, i.e. different<br> ⇒ entropy $H = 0.5\text{ bit/source symbol}$ ⇒ the source is redundant. | ||
| + | * $\rm BQ2$: $p_{\rm A} = p_{\rm B} = 0.5$ (equally probable)<br> ⇒ entropy $H = 1\text{ bit/source symbol}$ ⇒ the source is redundancy-free. | ||
| + | * $\rm BQ3$: There is no concrete information on the statistics here. <br>In subtask '''(6)''' you are to estimate the entropy $H$ of this source. | ||
| − | |||
| − | + | For these three sources, the respective "residual redundancy" $r(N)$ was determined by simulation, which remains in the binary sequence after [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#The_Lempel-Ziv-Welch_algorithm |Lempel–Ziv–Welch coding]]. | |
| − | + | The results are shown in the first column of the above table for the sources | |
| + | *$\rm BQ1$ (yellow background), | ||
| + | *$\rm BQ2$ (green background) and | ||
| + | *$\rm BQ3$ (blue background) | ||
| − | |||
| − | + | whereby we have restricted ourselves to sequence lengths $N ≤ 50000$ in the simulation. | |
| − | + | The "relative redundancy of the output sequence" – simplified called "residual redundancy" – can be calculated from | |
| + | * the length $N$ of the input sequence, | ||
| + | * the length $L(N)$ of the output sequence and | ||
| + | *the entropy $H$ | ||
| − | |||
| − | : | + | in the following way: |
| − | + | :$$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$ | |
| − | : | ||
| − | |||
| − | |||
| − | + | This takes into account that with perfect source coding the length of the output sequence could be lowered to the value $L_{\rm min} = N · H$ . | |
| + | *With non-perfect source coding, $L(n) - N · H$ gives the remaining redundancy (with the pseudo–unit "bit"). | ||
| + | *After dividing by $L(n)$, one obtains the relative redundancy $r(n)$ with the value range between zero and one; $r(n)$ should be as small as possible. | ||
| − | |||
| − | + | A second parameter for measuring the efficiency of LZW coding is the "compression factor" $K(N)$ as the quotient of the lengths of the output and input sequences, which should also be very small: | |
| − | |||
| − | |||
| − | |||
:$$K(N) = {L(N) }/{N} \hspace{0.05cm},$$ | :$$K(N) = {L(N) }/{N} \hspace{0.05cm},$$ | ||
| − | |||
| − | + | In the [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Quantitative_statements_on_asymptotic_optimality|theory section]] it was shown that the residual redundancy $r(n)$ is well approximated by the function | |
| − | :$$r'(N) ={A} | + | :$$r\hspace{0.05cm}'(N) =\frac {A}{{\rm lg}\hspace{0.1cm}(N)} |
\hspace{0.5cm}{\rm mit}\hspace{0.5cm} A = 4 \cdot {r(N = 10000)} | \hspace{0.5cm}{\rm mit}\hspace{0.5cm} A = 4 \cdot {r(N = 10000)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| + | *This approximation $r\hspace{0.05cm}'(N)$ is given for $\rm BQ1$ in the second column of the table above. | ||
| + | * In subtasks '''(4)''' and '''(5)''' you are to make the approximation for sources $\rm BQ2$ and $\rm BQ3$ . | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The task belongs to the chapter [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch|Compression according to Lempel, Ziv and Welch]]. | ||
| + | *In particular, reference is made to the pages | ||
| + | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Remaining_redundancy_as_a_measure_for_the_efficiency_of_coding_methods|Remaining redundancy as a measure for the efficiency of coding methods]], | ||
| + | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Efficiency_of_Lempel-Ziv_coding|Efficiency of Lempel-Ziv coding]] and | ||
| + | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Quantitative_statements_on_asymptotic_optimality|Quantitative statements on asymptotic optimality]]. | ||
| + | *The descriptive variables $K(N)$ and $r(N)$ are deterministically related. | ||
| + | |||
| − | === | + | |
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {With which parameter $A$ was the approximation $r\hspace{0.05cm}'(N)$ of the residual redundancy for the binary source $\rm BQ1$ created? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A \ = \ $ { 1.06 3% } |
| − | { | + | {What is the minimum size of $N = N_2$ for $\rm BQ1$ so that the residual redundancy satisfies the condition $r(N) ≈ r\hspace{0.05cm}'(N) \le 5\%$ ? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $N_{2} \ = \ $ { 1.58 3% } $\ \cdot 10^{21}$ |
| − | { | + | {What is the minimum size of $N = N_3$ at $\rm BQ1$ so that the compression factor $K(N)= L(N)/N$ is not greater than $0.6$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $N_{3} \ = \ $ { 2.29 3% } $\ \cdot 10^{6}$ |
| − | { | + | {Now determine the redundancy approximation $r\hspace{0.05cm}'(N)$ for the redundancy-free binary source $\rm BQ2$, in particular: |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $r'(N = 50000)\ = \ $ { 0.162 3% } |
| − | $r'(N = 10^6)$ | + | $r'(N = 10^6)\ = \ $ { 0.127 3% } |
| − | $r'(N = 10^12)$ | + | $r'(N = 10^{12})\ = \ $ { 0.063 3% } |
| − | { | + | {What values does the redundancy approximation $r\hspace{0.05cm}'(N)$ yield for the unspecified binary source $\rm BQ3$? In particular: |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $r'(N = 50000)\ = \ $ { 0.289 3% } |
| − | $r'(N = 10^6)$ | + | $r'(N = 10^6)\ = \ $ { 0.227 3% } |
| − | $r'(N = 10^12)$ | + | $r'(N = 10^{12})\ = \ $ { 0.113 3% } |
| − | { | + | {According to this result, what source entropy $H$ could $\rm BQ3$ ? <u>Hint:</u> Exactly one answer is correct. |
| − | |type=" | + | |type="()"} |
| − | - | + | - $H = 1.00 \ \rm bit/source\hspace{0.15cm}symbol$, |
| − | - | + | - $H = 0.75 \ \rm bit/source\hspace{0.15cm} symbol$, |
| − | - | + | - $H = 0.50 \ \rm bit/source\hspace{0.15cm} symbol$, |
| − | + | + | + $H = 0.25 \ \rm bit/source\hspace{0.15cm} symbol$. |
| Line 90: | Line 107: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' The approximation $r\hspace{0.05cm}'(N)$ agrees exactly by definition for the sequence length $N = 10000$ with the residual redundancy $r(N) = 0.265$ determined by simulation. | |
| + | *Thus | ||
:$$A = 4 \cdot r(N = 10000) =4 \cdot {0.265} \hspace{0.15cm}\underline{= 1.06} | :$$A = 4 \cdot r(N = 10000) =4 \cdot {0.265} \hspace{0.15cm}\underline{= 1.06} | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | + | ||
| − | :$${{\rm lg}\hspace{0.1cm}N_{\rm | + | |
| − | N_{\rm | + | '''(2)''' From the relationship ${A}/{\rm lg}\hspace{0.1cm}(N) ≤ 0.05$ ⇒ ${A}/{\rm lg}\hspace{0.1cm}(N) = 0.05$ it follows: |
| + | :$${{\rm lg}\hspace{0.1cm}N_{\rm 2}} = \frac{A}{0.05} = 21.2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
| + | N_{\rm 2} = 10^{21.2} \hspace{0.15cm}\underline{= 1.58 \cdot 10^{21}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| − | + | ||
| − | \hspace{0.05cm}. $$ | + | '''(3)''' In general, $r(N) = 1 - {H}/{K(N)} \hspace{0.05cm}.$ |
| − | + | *$\rm BQ1$ has entropy $H = 0.5$ bit/source symbol. | |
| − | :$$r(N_{\rm | + | *It follows that because $r(N) ≈ r\hspace{0.05cm}'(N)$ for $K(N_3) = 0.6$: |
| − | {\rm lg}\hspace{0.1cm}N_{\rm | + | :$$r(N_{\rm 3}) = 1 - \frac{0.5}{0.6} = 0.167 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} |
| + | {\rm lg}\hspace{0.1cm}N_{\rm 3} = \frac{A}{0.167} = 6.36 | ||
\hspace{0.1cm}\Rightarrow\hspace{0.1cm} | \hspace{0.1cm}\Rightarrow\hspace{0.1cm} | ||
| − | N_{\rm | + | N_{\rm 3} = 10^{6.36} \hspace{0.15cm}\underline{= 2.29 \cdot 10^{6}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | : | + | |
| + | |||
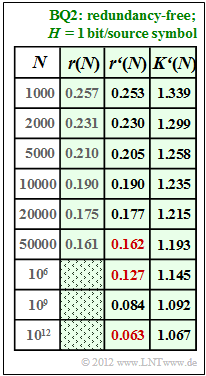
| + | [[File:EN_Inf_A_2_5d_v2.png|right|frame|Results for $\rm BQ2$]] | ||
| + | '''(4)''' For $N = 10000$ ⇒ $r(N) ≈ r\hspace{0.05cm}'(N) = 0.19$: | ||
:$$\frac{A}{{\rm lg}\hspace{0.1cm}10000} = 0.19 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | :$$\frac{A}{{\rm lg}\hspace{0.1cm}10000} = 0.19 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
A = 0.19 \cdot 4 = 0.76 \hspace{0.05cm}. $$ | A = 0.19 \cdot 4 = 0.76 \hspace{0.05cm}. $$ | ||
| − | : | + | *The results are summarised in the table opposite. |
| + | *One can see the very good agreement between $r(N)$ and $r\hspace{0.05cm}'(N)$. | ||
| + | *The numerical values sought are marked in red in the table: | ||
| + | $$r'(N = 50000)\hspace{0.15cm}\underline{ = 0.162},\hspace{0.3cm}r'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.127},\hspace{0.3cm} | ||
| + | r'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.063}.$$ | ||
| + | |||
| + | *For the compression factor – the apostrophe indicates that the approximation $r\hspace{0.05cm}'(N)$ was assumed: | ||
| + | :$$K\hspace{0.05cm}'(N) = \frac{1}{1 - r\hspace{0.05cm}'(N)}\hspace{0.05cm}.$$ | ||
| + | *Thus, for the length of the LZW output string: | ||
| + | :$$L\hspace{0.05cm}'(N) = K\hspace{0.05cm}'(N) \cdot N = \frac{N}{1 - r\hspace{0.05cm}'(N)}\hspace{0.05cm}.$$ | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
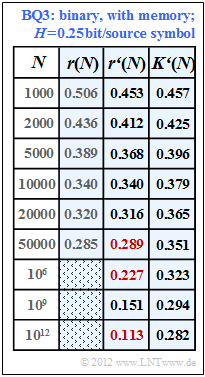
| − | : | + | [[File:EN_Inf_A_2_5e_v2.png|right|frame|Results for $\rm BQ3$]] |
| − | + | '''(5)''' Following a similar procedure as in subtask '''(4)''' we obtain the fitting parameter $A = 1.36$ for the binary source $\rm BQ3$ and from this the results according to the table with a blue background. | |
| − | + | <u>Hint:</u> The last column of this table is only understandable with knowledge of subtask '''(6)'''. There it is shown that the source $\rm BQ3$ has the entropy $H = 0.25$ bit/source symbol. | |
| − | + | *In this case, the following applies to the compression factor: | |
| − | :$$K'(N) = \frac{H}{1 - r'(N)} = \frac{0.25}{1 - r'(N)} \hspace{0.05cm}.$$ | + | :$$K\hspace{0.05cm}'(N) = \frac{H}{1 - r\hspace{0.05cm}'(N)} = \frac{0.25}{1 - r'(N)} \hspace{0.05cm}.$$ |
| − | + | *Thus, for the values of residual redundancy we are looking for, we obtain: | |
| − | + | :$$r\hspace{0.05cm}'(N = 50000)\hspace{0.15cm}\underline{ = 0.289},\hspace{0.3cm}r\hspace{0.05cm}'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.227},\hspace{0.3cm} | |
| + | r\hspace{0.05cm}'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.113}.$$ | ||
| + | *Thus, for $N = 10^{12}$ , the compression factor $(0.282)$ still deviates significantly from the entropy $(0.25)$ which can only be achieved for $N \to \infty$ ("Source Coding Theorem"). | ||
| − | |||
| − | |||
| − | |||
| − | : | + | '''(6)''' The individual approximations $r\hspace{0.05cm}'(N)$ differ only by the parameter $A$. Here we found: |
| + | # Source $\rm BQ1$ with $H = 0.50$ ⇒ $A = 1.06$ ⇒ according to the specification sheet, | ||
| + | # Source $\rm BQ2$ with $H = 1.00$ ⇒ $A = 0.76$ ⇒ see subtask '''(4)''', | ||
| + | # Source $\rm BQ3$ $(H$ unknown$)$: $A = 4 · 0.34 =1.36$ ⇒ corresponding to the table on the right. | ||
| − | + | *Obviously, the smaller the entropy $H$ the larger the adjustment factor $A$ (and vice versa). | |
| + | *Since exactly one solution is possible, $H = 0.25$ bit/source symbol must be correct ⇒ <u>answer 4</u>. | ||
| − | + | *In fact, the probabilities $p_{\rm A} = 0.96$ and $p_{\rm B} = 0.04$ ⇒ $H ≈ 0.25$ were used in the simulation for the source $\rm BQ3$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^2.2 Lempel-Ziv-Welch Compression^]] |
Latest revision as of 13:12, 10 August 2021
We assume here a binary input sequence of length $N$ and consider three different binary sources:
- $\rm BQ1$: Symbol probabilities $p_{\rm A} = 0.89$ and $p_{\rm B} = 0.11$, i.e. different
⇒ entropy $H = 0.5\text{ bit/source symbol}$ ⇒ the source is redundant. - $\rm BQ2$: $p_{\rm A} = p_{\rm B} = 0.5$ (equally probable)
⇒ entropy $H = 1\text{ bit/source symbol}$ ⇒ the source is redundancy-free. - $\rm BQ3$: There is no concrete information on the statistics here.
In subtask (6) you are to estimate the entropy $H$ of this source.
For these three sources, the respective "residual redundancy" $r(N)$ was determined by simulation, which remains in the binary sequence after Lempel–Ziv–Welch coding.
The results are shown in the first column of the above table for the sources
- $\rm BQ1$ (yellow background),
- $\rm BQ2$ (green background) and
- $\rm BQ3$ (blue background)
whereby we have restricted ourselves to sequence lengths $N ≤ 50000$ in the simulation.
The "relative redundancy of the output sequence" – simplified called "residual redundancy" – can be calculated from
- the length $N$ of the input sequence,
- the length $L(N)$ of the output sequence and
- the entropy $H$
in the following way:
- $$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$
This takes into account that with perfect source coding the length of the output sequence could be lowered to the value $L_{\rm min} = N · H$ .
- With non-perfect source coding, $L(n) - N · H$ gives the remaining redundancy (with the pseudo–unit "bit").
- After dividing by $L(n)$, one obtains the relative redundancy $r(n)$ with the value range between zero and one; $r(n)$ should be as small as possible.
A second parameter for measuring the efficiency of LZW coding is the "compression factor" $K(N)$ as the quotient of the lengths of the output and input sequences, which should also be very small:
- $$K(N) = {L(N) }/{N} \hspace{0.05cm},$$
In the theory section it was shown that the residual redundancy $r(n)$ is well approximated by the function
- $$r\hspace{0.05cm}'(N) =\frac {A}{{\rm lg}\hspace{0.1cm}(N)} \hspace{0.5cm}{\rm mit}\hspace{0.5cm} A = 4 \cdot {r(N = 10000)} \hspace{0.05cm}.$$
- This approximation $r\hspace{0.05cm}'(N)$ is given for $\rm BQ1$ in the second column of the table above.
- In subtasks (4) and (5) you are to make the approximation for sources $\rm BQ2$ and $\rm BQ3$ .
Hints:
- The task belongs to the chapter Compression according to Lempel, Ziv and Welch.
- In particular, reference is made to the pages
- The descriptive variables $K(N)$ and $r(N)$ are deterministically related.
Questions
Solution
- Thus
- $$A = 4 \cdot r(N = 10000) =4 \cdot {0.265} \hspace{0.15cm}\underline{= 1.06} \hspace{0.05cm}. $$
(2) From the relationship ${A}/{\rm lg}\hspace{0.1cm}(N) ≤ 0.05$ ⇒ ${A}/{\rm lg}\hspace{0.1cm}(N) = 0.05$ it follows:
- $${{\rm lg}\hspace{0.1cm}N_{\rm 2}} = \frac{A}{0.05} = 21.2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} N_{\rm 2} = 10^{21.2} \hspace{0.15cm}\underline{= 1.58 \cdot 10^{21}} \hspace{0.05cm}.$$
(3) In general, $r(N) = 1 - {H}/{K(N)} \hspace{0.05cm}.$
- $\rm BQ1$ has entropy $H = 0.5$ bit/source symbol.
- It follows that because $r(N) ≈ r\hspace{0.05cm}'(N)$ for $K(N_3) = 0.6$:
- $$r(N_{\rm 3}) = 1 - \frac{0.5}{0.6} = 0.167 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} {\rm lg}\hspace{0.1cm}N_{\rm 3} = \frac{A}{0.167} = 6.36 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} N_{\rm 3} = 10^{6.36} \hspace{0.15cm}\underline{= 2.29 \cdot 10^{6}} \hspace{0.05cm}.$$
(4) For $N = 10000$ ⇒ $r(N) ≈ r\hspace{0.05cm}'(N) = 0.19$:
- $$\frac{A}{{\rm lg}\hspace{0.1cm}10000} = 0.19 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.19 \cdot 4 = 0.76 \hspace{0.05cm}. $$
- The results are summarised in the table opposite.
- One can see the very good agreement between $r(N)$ and $r\hspace{0.05cm}'(N)$.
- The numerical values sought are marked in red in the table:
$$r'(N = 50000)\hspace{0.15cm}\underline{ = 0.162},\hspace{0.3cm}r'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.127},\hspace{0.3cm} r'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.063}.$$
- For the compression factor – the apostrophe indicates that the approximation $r\hspace{0.05cm}'(N)$ was assumed:
- $$K\hspace{0.05cm}'(N) = \frac{1}{1 - r\hspace{0.05cm}'(N)}\hspace{0.05cm}.$$
- Thus, for the length of the LZW output string:
- $$L\hspace{0.05cm}'(N) = K\hspace{0.05cm}'(N) \cdot N = \frac{N}{1 - r\hspace{0.05cm}'(N)}\hspace{0.05cm}.$$
(5) Following a similar procedure as in subtask (4) we obtain the fitting parameter $A = 1.36$ for the binary source $\rm BQ3$ and from this the results according to the table with a blue background.
Hint: The last column of this table is only understandable with knowledge of subtask (6). There it is shown that the source $\rm BQ3$ has the entropy $H = 0.25$ bit/source symbol.
- In this case, the following applies to the compression factor:
- $$K\hspace{0.05cm}'(N) = \frac{H}{1 - r\hspace{0.05cm}'(N)} = \frac{0.25}{1 - r'(N)} \hspace{0.05cm}.$$
- Thus, for the values of residual redundancy we are looking for, we obtain:
- $$r\hspace{0.05cm}'(N = 50000)\hspace{0.15cm}\underline{ = 0.289},\hspace{0.3cm}r\hspace{0.05cm}'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.227},\hspace{0.3cm} r\hspace{0.05cm}'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.113}.$$
- Thus, for $N = 10^{12}$ , the compression factor $(0.282)$ still deviates significantly from the entropy $(0.25)$ which can only be achieved for $N \to \infty$ ("Source Coding Theorem").
(6) The individual approximations $r\hspace{0.05cm}'(N)$ differ only by the parameter $A$. Here we found:
- Source $\rm BQ1$ with $H = 0.50$ ⇒ $A = 1.06$ ⇒ according to the specification sheet,
- Source $\rm BQ2$ with $H = 1.00$ ⇒ $A = 0.76$ ⇒ see subtask (4),
- Source $\rm BQ3$ $(H$ unknown$)$: $A = 4 · 0.34 =1.36$ ⇒ corresponding to the table on the right.
- Obviously, the smaller the entropy $H$ the larger the adjustment factor $A$ (and vice versa).
- Since exactly one solution is possible, $H = 0.25$ bit/source symbol must be correct ⇒ answer 4.
- In fact, the probabilities $p_{\rm A} = 0.96$ and $p_{\rm B} = 0.04$ ⇒ $H ≈ 0.25$ were used in the simulation for the source $\rm BQ3$.