Difference between revisions of "Aufgaben:Exercise 3.8Z: Tuples from Ternary Random Variables"
From LNTwww
| (25 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Different_Entropy_Measures_of_Two-Dimensional_Random_Variables |
}} | }} | ||
| − | [[File:P_ID2771__Inf_Z_3_7.png|right|]] | + | [[File:P_ID2771__Inf_Z_3_7.png|right|2D random variable $XY$]] |
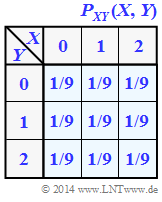
| − | + | We consider the tuple $Z = (X, Y)$, where the individual components $X$ and $Y$ each represent ternary random variables ⇒ symbol set size $|X| = |Y| = 3$. The joint probability function $P_{ XY }(X, Y)$ is sketched on the right. | |
| − | In | + | In this exercise, the following entropies are to be calculated: |
| − | + | * the "joint entropy" $H(XY)$ and the "mutual information" $I(X; Y)$, | |
| − | + | * the "joint entropy" $H(XZ)$ and the "mutual information" $I(X; Z)$, | |
| − | + | * the two "conditional entropies" $H(Z|X)$ and $H(X|Z)$. | |
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Information_Theory/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen|Different entropies of two-dimensional random variables]]. | ||
| + | *In particular, reference is made to the pages <br> [[Information_Theory/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Conditional_probability_and_conditional_entropy|Conditional probability and conditional entropy]] as well as <br> [[Information_Theory/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Mutual_information_between_two_random_variables|Mutual information between two random variables]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the following entropies. |
| + | |type="{}"} | ||
| + | $H(X)\ = \ $ { 1.585 3% } $\ \rm bit$ | ||
| + | $H(Y)\ = \ $ { 1.585 3% } $\ \rm bit$ | ||
| + | $ H(XY)\ = \ $ { 3.17 3% } $\ \rm bit$ | ||
| + | |||
| + | {What is the mutual information between the random variables $X$ and $Y$? | ||
|type="{}"} | |type="{}"} | ||
| − | $ H(X)$ | + | $I(X; Y)\ = \ $ { 0. } $\ \rm bit$ |
| + | |||
| + | {What is the mutual information between the random variables $X$ and $Z$? | ||
| + | |type="{}"} | ||
| + | $I(X; Z)\ = \ $ { 1.585 3% } $\ \rm bit$ | ||
| + | |||
| + | {What conditional entropies exist between $X$ and $Z$? | ||
| + | |type="{}"} | ||
| + | $H(Z|X)\ = \ $ { 1.585 3% } $\ \rm bit$ | ||
| + | $ H(X|Z)\ = \ $ { 0. } $\ \rm bit$ | ||
| Line 27: | Line 52: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' For the random variables $X =\{0,\ 1,\ 2\}$ ⇒ $|X| = 3$ and $Y = \{0,\ 1,\ 2\}$ ⇒ $|Y| = 3$ there is a uniform distribution in each case. |
| − | '''2 | + | *Thus one obtains for the entropies: |
| − | '''3 | + | |
| − | '''4 | + | :$$H(X) = {\rm log}_2 \hspace{0.1cm} (3) |
| − | + | \hspace{0.15cm}\underline{= 1.585\,{\rm (bit)}} \hspace{0.05cm},$$ | |
| − | + | :$$H(Y) = {\rm log}_2 \hspace{0.1cm} (3) | |
| − | + | \hspace{0.15cm}\underline{= 1.585\,{\rm (bit)}}\hspace{0.05cm}.$$ | |
| + | |||
| + | *The two-dimensional random variable $XY = \{00,\ 01,\ 02,\ 10,\ 11,\ 12,\ 20,\ 21,\ 22\}$ ⇒ $|XY| = |Z| = 9$ has also equal probabilities: | ||
| + | :$$p_{ 00 } = p_{ 01 } =\text{...} = p_{ 22 } = 1/9.$$ | ||
| + | *From this follows: | ||
| + | :$$H(XY) = {\rm log}_2 \hspace{0.1cm} (9) \hspace{0.15cm}\underline{= 3.170\,{\rm (bit)}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' The random variables $X$ and $Y$ are statistically independent because of $P_{ XY }(⋅) = P_X(⋅) · P_Y(⋅)$ . | ||
| + | *From this follows $I(X, Y)\hspace{0.15cm}\underline{ = 0}$. | ||
| + | *The same result is obtained by the equation $I(X; Y) = H(X) + H(Y) - H(XY)$. | ||
| + | |||
| + | |||
| + | |||
| + | [[File:P_ID2774__Inf_Z_3_7c.png|right|frame|Probability mass function of the random variable $XZ$]] | ||
| + | |||
| + | '''(3)''' If one interprets $I(X; Z)$ as the remaining uncertainty with regard to the tuple $Z$, when the first component $X$ is known, then the following obviously applies: | ||
| + | :$$ I(X; Z) = H(Y)\hspace{0.15cm}\underline{ = 1.585 \ \rm bit}.$$ | ||
| + | |||
| + | In purely formal terms, this task can also be solved as follows: | ||
| + | * The entropy $H(Z)$ is equal to the joint entropy $H(XY) = 3.17 \ \rm bit$. | ||
| + | * The joint probability $P_{ XZ }(X, Z)$ contains nine elements of probability $1/9$, all others are occupied by zeros ⇒ $H(XZ) = \log_2 (9) = 3.170 \ \rm bit $. | ||
| + | * Thus, the following applies to the mutual information of the random variables $X$ and $Z$: | ||
| + | :$$I(X;Z) = H(X) + H(Z) - H(XZ) = 1.585 + 3.170- 3.170\hspace{0.15cm} \underline {= 1.585\,{\rm (bit)}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | [[File:P_ID2773__Inf_Z_3_7d.png|right|frame|Entropies of the 2D variable $XZ$]] | ||
| + | '''(4)''' According to the second graph: | ||
| + | :$$H(Z \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(XZ) - H(X) = 3.170-1.585\hspace{0.15cm} \underline {=1.585\ {\rm (bit)}} \hspace{0.05cm},$$ | ||
| + | :$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Z) = H(XZ) - H(Z) = 3.170-3.170\hspace{0.15cm} \underline {=0\ {\rm (bit)}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | * $H(Z|X)$ gives the residual uncertainty with respect to the tuple $Z$, when the first componen $X$ is known. | ||
| + | * The uncertainty regarding the tuple $Z$ is $H(Z) = 2 · \log_2 (3) \ \rm bit$. | ||
| + | * When the component $X$ is known, the uncertainty is halved to $H(Z|X) = \log_2 (3)\ \rm bit$. | ||
| + | * $H(X|Z)$ gives the remaining uncertainty with respect to component $X$, when the tuple $Z = (X, Y)$ is known. | ||
| + | * This uncertainty is of course zero: If one knows $Z$, one also knows $X$. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^3.2 Entropies of 2D Random Variables^]] |
| − | ^]] | ||
Latest revision as of 09:16, 24 September 2021
We consider the tuple $Z = (X, Y)$, where the individual components $X$ and $Y$ each represent ternary random variables ⇒ symbol set size $|X| = |Y| = 3$. The joint probability function $P_{ XY }(X, Y)$ is sketched on the right.
In this exercise, the following entropies are to be calculated:
- the "joint entropy" $H(XY)$ and the "mutual information" $I(X; Y)$,
- the "joint entropy" $H(XZ)$ and the "mutual information" $I(X; Z)$,
- the two "conditional entropies" $H(Z|X)$ and $H(X|Z)$.
Hints:
- The exercise belongs to the chapter Different entropies of two-dimensional random variables.
- In particular, reference is made to the pages
Conditional probability and conditional entropy as well as
Mutual information between two random variables.
Questions
Solution
(1) For the random variables $X =\{0,\ 1,\ 2\}$ ⇒ $|X| = 3$ and $Y = \{0,\ 1,\ 2\}$ ⇒ $|Y| = 3$ there is a uniform distribution in each case.
- Thus one obtains for the entropies:
- $$H(X) = {\rm log}_2 \hspace{0.1cm} (3) \hspace{0.15cm}\underline{= 1.585\,{\rm (bit)}} \hspace{0.05cm},$$
- $$H(Y) = {\rm log}_2 \hspace{0.1cm} (3) \hspace{0.15cm}\underline{= 1.585\,{\rm (bit)}}\hspace{0.05cm}.$$
- The two-dimensional random variable $XY = \{00,\ 01,\ 02,\ 10,\ 11,\ 12,\ 20,\ 21,\ 22\}$ ⇒ $|XY| = |Z| = 9$ has also equal probabilities:
- $$p_{ 00 } = p_{ 01 } =\text{...} = p_{ 22 } = 1/9.$$
- From this follows:
- $$H(XY) = {\rm log}_2 \hspace{0.1cm} (9) \hspace{0.15cm}\underline{= 3.170\,{\rm (bit)}} \hspace{0.05cm}.$$
(2) The random variables $X$ and $Y$ are statistically independent because of $P_{ XY }(⋅) = P_X(⋅) · P_Y(⋅)$ .
- From this follows $I(X, Y)\hspace{0.15cm}\underline{ = 0}$.
- The same result is obtained by the equation $I(X; Y) = H(X) + H(Y) - H(XY)$.
(3) If one interprets $I(X; Z)$ as the remaining uncertainty with regard to the tuple $Z$, when the first component $X$ is known, then the following obviously applies:
- $$ I(X; Z) = H(Y)\hspace{0.15cm}\underline{ = 1.585 \ \rm bit}.$$
In purely formal terms, this task can also be solved as follows:
- The entropy $H(Z)$ is equal to the joint entropy $H(XY) = 3.17 \ \rm bit$.
- The joint probability $P_{ XZ }(X, Z)$ contains nine elements of probability $1/9$, all others are occupied by zeros ⇒ $H(XZ) = \log_2 (9) = 3.170 \ \rm bit $.
- Thus, the following applies to the mutual information of the random variables $X$ and $Z$:
- $$I(X;Z) = H(X) + H(Z) - H(XZ) = 1.585 + 3.170- 3.170\hspace{0.15cm} \underline {= 1.585\,{\rm (bit)}} \hspace{0.05cm}.$$
(4) According to the second graph:
- $$H(Z \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(XZ) - H(X) = 3.170-1.585\hspace{0.15cm} \underline {=1.585\ {\rm (bit)}} \hspace{0.05cm},$$
- $$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Z) = H(XZ) - H(Z) = 3.170-3.170\hspace{0.15cm} \underline {=0\ {\rm (bit)}} \hspace{0.05cm}.$$
- $H(Z|X)$ gives the residual uncertainty with respect to the tuple $Z$, when the first componen $X$ is known.
- The uncertainty regarding the tuple $Z$ is $H(Z) = 2 · \log_2 (3) \ \rm bit$.
- When the component $X$ is known, the uncertainty is halved to $H(Z|X) = \log_2 (3)\ \rm bit$.
- $H(X|Z)$ gives the remaining uncertainty with respect to component $X$, when the tuple $Z = (X, Y)$ is known.
- This uncertainty is of course zero: If one knows $Z$, one also knows $X$.