Loading [MathJax]/jax/output/HTML-CSS/fonts/TeX/fontdata.js

Difference between revisions of "Aufgaben:Exercise 5.4: Walsh Functions (PCCF, PACF)"

From LNTwww
 
(19 intermediate revisions by 4 users not shown)
Line 1: Line 1:
  
−
{{quiz-Header|Buchseite=Modulationsverfahren/Spreizfolgen für CDMA
+
{{quiz-Header|Buchseite=Modulation_Methods/Spreading_Sequences_for_CDMA
 
}}
 
}}
  
−
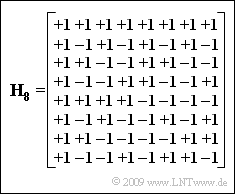
[[File:P_ID1889__Mod_A_5_4.png|right|]]
+
[[File:P_ID1889__Mod_A_5_4.png|right|frame|Hadamard matrix  H8]]
−
Häufig verwendet man zur Bandspreizung und Bandstauchung so genannte ''Walsh–Funktionen'', die mittels der Hadamard–Matrix konstruiert werden können. Ausgehend von der Matrix
+
The so-called  "Walsh functions",  which can be constructed by means of the Hadamard matrix,  are often used for band spreading and band compression.  Starting from the matrix
−
H2=[+1+1+1−1]
+
:H2=[+1+1+1−1]
−
lassen sich durch folgende rekursive Berechnungsvorschrift die weiteren Hadamard–Matrizen H4, H8, usw. herleiten:
+
the further Hadamard matrices  H4,  H8,  etc. can be derived by the following recursion:
−
H2J=[HJHJHJ−HJ].
+
:H2J=[HJHJHJ−HJ].
−
Die Grafik zeigt die Matrix $H_8$ für den Spreizfaktor J = 8. Daraus lassen sich die Spreizfolgen
+
The diagram shows the matrix  $ {\mathbf{H}_{8}}$  for the spreading factor  $J = 8$.  From this we can derive the spreading sequences
−
⟨w(1)ν⟩=+1−1+1−1+1−1+1−1,
+
:⟨w(1)ν⟩=+1−1+1−1+1−1+1−1,
−
⟨w(2)ν⟩=+1+1−1−1+1+1−1−1,
+
:⟨w(2)ν⟩=+1+1−1−1+1+1−1−1,
−
...
+
:...
−
$$\langle w_\nu^{(7)}\rangle  =  {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$
+
:$$\langle w_\nu^{(7)}\rangle  =  {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}$$
−
für sieben CDMA–Teilnehmer ablesen. Die Spreizfolge 〈$w_ν^{(0)}$〉 entsprechend der ersten Zeile in der Hadamard–Matrix wird meistens nicht vergeben, da sie nicht wirklich spreizt.
+
for seven CDMA subscribers.  The spreading sequence  $ \langle w_\nu^{(0)}\rangle$  corresponding to the first row in the Hadamard matrix is usually not assigned because it does not spread.
  
−
Die Fragen beziehen sich meist auf den Spreizfaktor J = 4. Damit können entsprechend mit den Spreizfolgen 〈$w_ν{(1)}$〉, 〈$w_ν{(2)}$〉 und 〈$w_ν{(3)}$〉 maximal drei CDMA–Teilnehmer versorgt werden, die sich aus der zweiten, dritten und vierten Zeile der Matrix $H_4$ ergeben.
+
The questions mostly refer to the spreading factor  $J = 4$.  Thus,  correspondingly,  a maximum of three CDMA subscribers can be supplied with the spreading sequences  $ \langle w_\nu^{(1)}\rangle$,  $ \langle w_\nu^{(2)}\rangle$  and  $ \langle w_\nu^{(3)}\rangle$,  which result from the second, third and fourth rows of the matrix $ {\mathbf{H}_{4}}$.
  
−
Hinsichtlich der Korrelationsfunktionen soll in dieser Aufgabe folgende Nomenklatur gelten:
+
Regarding the correlation functions, the following nomenclature shall apply in this exercise:
−
:* Die periodische Kreuzkorrelationsfunktion (PKKF) zwischen den Folgen 〈$w_ν{(i)}$〉 und 〈$w_ν{(j)}$〉 wird mit φ_{ij}(λ) bezeichnet. Hierbei gilt:
+
* The  [[Modulation_Methods/Spreading_Sequences_for_CDMA#Periodic_ACF_and_CCF|periodic cross-correlation function]]  $\rm (PCCF)$  between the sequences  $ \langle w_\nu^{(i)}\rangle$  and  $ \langle w_\nu^{(j)}\rangle$  is denoted by  φ_{ij}(λ).   Here:
−
{\it \varphi}_{ij}(\lambda) = {\rm E}\left [ w_{\nu}^{(i)} \cdot w_{\nu+ \lambda}^{(j)} \right ] \hspace{0.05cm}.
+
:{\it \varphi}_{ij}(\lambda) = {\rm E}\left [ w_{\nu}^{(i)} \cdot w_{\nu+ \lambda}^{(j)} \right ] \hspace{0.05cm}.
−
:* Ist die PKKF $φ_{ij}(λ)$ identisch 0 (das heißt: φ_{ij}(λ) = 0 für alle Werte von λ), so stören sich die CDMA–Teilnehmer nicht, auch wenn zwei Teilnehmer unterschiedliche Laufzeiten aufweisen.
+
* If  $φ_{ij} \equiv 0  ($that is:  φ_{ij}(λ) = 0  for all values of  $λ)$,  the CDMA subscribers do not interfere with each other,  even if they have different propagation times.
−
:* Gilt wenigstens φ_{ij}(λ = 0) = 0, so kommt es zumindest bei synchronem CDMA–Betrieb (keine oder gleiche Laufzeiten aller Teilnehmer) zu keinen Interferenzen.
+
* If at least  $φ_{ij}({\it λ} = 0) = 0$  applies,  then no interference occurs,  at least in synchronous CDMA operation  $(no or equal propagation times of all subscribers).$ 
−
:* Die periodischen Autokorrelationsfunktionen (PAKF) der Walsh–Funktion 〈$w_ν{(i)}$〉 wird mit φ_{ii}(λ) bezeichnet. Es gilt:
+
* The  [[Modulation_Methods/Spreading_Sequences_for_CDMA#Periodic_ACF_and_CCF|periodic auto-correlation function]]  $\rm (PACF)$  of the Walsh function  $ \langle w_\nu^{(i)}\rangle$  is denoted by  φ_{ii}(λ),  and it holds:
−
{\it \varphi}_{ii}(\lambda) = {\rm E}\left [ w_{\nu}^{(i)} \cdot w_{\nu+ \lambda}^{(i)} \right ] \hspace{0.05cm}.
+
:{\it \varphi}_{ii}(\lambda) = {\rm E}\left [ w_{\nu}^{(i)} \cdot w_{\nu+ \lambda}^{(i)} \right ] \hspace{0.05cm}.
−
'''Hinweis:''' Die Aufgabe bezieht sich auf das [http://en.lntwww.de/Modulationsverfahren/Spreizfolgen_f%C3%BCr_CDMA Kapitel 5.3]. Die Abszisse ist auf die Chipdauer T_c normiert. Das bedeutet, dass λ = 1 eigentlich eine Verschiebung um die Verzögerungszeit τ = T_c beschreibt.
 
  
  
  
−
===Fragebogen===
+
Notes:
 +
*The exercise belongs to the chapter  [[Modulation_Methods/Spreizfolgen_für_CDMA|Spreading Sequences for CDMA]].
 +
*Reference is made in particular to the section  [[Modulation_Methods/Spreading_Sequences_for_CDMA#Walsh_functions|Walsh functions]]  in the theory part.
 +
* We would also like to draw your attention to the interactive applet  [[Applets:Generation_of_Walsh_functions|Generation of Walsh functions]]. 
 +
*The abscissa is normalized to the chip duration  T_c.  This means that  $λ = 1  actually describes a shift by the delay time  τ = T_c$. 
 +
 
 +
 
 +
 
 +
===Questions===
  
 
<quiz display=simple>
 
<quiz display=simple>
−
{Wie lauten die Spreizfolgen für J = 4?
+
{What are the spreading sequences for &nbsp;$J = 4$?
 
|type="[]"}
 
|type="[]"}
−
+ 〈$w_ν{(1)}$〉 = +1 –1 +1 –1,
+
+ $ \langle w_\nu^{(1)}\rangle = +\hspace{-0.05cm}1 -\hspace{-0.15cm}1 +\hspace{-0.15cm}1 -\hspace{-0.15cm}1$,
−
+ 〈$w_ν{(2)}$〉 = +1 +1 –1 –1,
+
+ $ \langle w_\nu^{(2)}\rangle = +\hspace{-0.05cm}1 +\hspace{-0.15cm}1 -\hspace{-0.15cm}1 -\hspace{-0.15cm}1$,
−
+ 〈$w_ν{(3)}〉 = +1 –1 –1 +1.
+
+ $ \langle w_\nu^{(3)}\rangle = +\hspace{-0.05cm}1 -\hspace{-0.15cm}1 -\hspace{-0.15cm}1 +\hspace{-0.15cm}1$.
  
−
{Welche Aussagen gelten bezüglich der PKKF–Werte φ_{ij}(λ = 0)?
+
{Which statements are true regarding the PCCF values &nbsp;φ_{ij}(λ = 0)?
 
|type="[]"}
 
|type="[]"}
−
+ Für J = 4 ist φ_{12}(λ = 0) = 0.
+
+ For $J = 4$,&nbsp; &nbsp;φ_{12}(λ = 0) = 0.
−
+ Für J = 4 ist φ_{13}(λ = 0) = 0.
+
+ For $J = 4$,&nbsp; &nbsp;φ_{13}(λ = 0) = 0.
−
+ Für J = 4 ist φ_{23}(λ = 0) = 0.
+
+ For $J = 4$,&nbsp; &nbsp;φ_{23}(λ = 0) = 0.
−
- Für J = 8 kann durchaus φ_{ij}(λ = 0) ≠ 0 gelten (i ≠ j).
+
- For $J = 8$,&nbsp; &nbsp;φ_{ij}(λ = 0) ≠ 0&nbsp; may well hold &nbsp;$(i ≠ j)$.
−
+ Bei synchronem CDMA stören sich die Teilnehmer nicht.
+
+ In synchronous CDMA,&nbsp; the subscribers do not interfere with each other.
  
−
{Welche Aussagen gelten für die PKKF–Werte mit λ ≠ 0?
+
{Which statements are true for the PCCF values with &nbsp;$λ ≠ 0$?
 
|type="[]"}
 
|type="[]"}
−
+ Die PKKF φ_{12}(λ) ist für alle Werte von λ gleich 0.
+
+ For all values of &nbsp;λ,&nbsp; the PCCF is &nbsp;$φ_{12}(λ) = 0$.
−
+ Die PKKF φ_{13}(λ) ist für alle Werte von λ gleich 0.
+
+ For all values of &nbsp;λ,&nbsp; the PCCF is &nbsp;$φ_{13}(λ) = 0$.
−
- Die PKKF φ_{23}(λ) ist für alle Werte von λ gleich 0
+
- For all values of &nbsp;λ,&nbsp; the PCCF is &nbsp;$φ_{23}(λ) = 0$.
−
- Bei asynchronem CDMA stören sich die Teilnehmer nicht.
+
- In asynchronous CDMA,&nbsp; the subscribers do not interfere with each other.
  
−
{Welche Aussagen gelten für die PAKF–Kurven?
+
{Which statements are true for the PACF curves?
 
|type="[]"}
 
|type="[]"}
−
+ Alle φ_{ii}(λ) sind periodisch.
+
+ All&nbsp; &nbsp;φ_{ii}(λ)&nbsp; curves are periodic.
−
+ Es gilt φ_{11}(λ = 0) = 1 und $φ_{11}(λ = 1) = –1$.
+
+ &nbsp;$φ_{11}(λ = 0) = +\hspace{-0.05cm}1$&nbsp; and &nbsp;$φ_{11}(λ = 1) = -\hspace{-0.05cm}1$&nbsp; hold.
−
- Es gilt φ_{22}(λ) = φ_{11}(λ).
+
- &nbsp;φ_{22}(λ) = φ_{11}(λ)&nbsp; holds.
−
+ Es gilt φ_{33}(λ) = φ_{22}(λ).
+
+ &nbsp;φ_{33}(λ) = φ_{22}(λ)&nbsp; holds.
 
</quiz>
 
</quiz>
  
−
===Musterlösung===
+
===Solution===
 
{{ML-Kopf}}
 
{{ML-Kopf}}
−
'''1.''' Die Matrix $H_4$ ist die linke obere Teilmatrix von $H_8$. Die Spreizfolgen ergeben sich aus den Zeilen 2, 3 und 4 von $H_4$, und stimmen mit den angegebenen Folgen überein. Somit sind alle Vorschläge richtig.
+
'''(1)'''&nbsp; <u>All solutions</u>&nbsp; are correct:
 +
*The matrix&nbsp; $ {\mathbf{H}_{4}}$&nbsp; is the upper left submatrix of&nbsp; $ {\mathbf{H}_{8}}$.  
 +
*The spreading sequences result from the rows 2,&nbsp; 3&nbsp; and 4&nbsp; of&nbsp; $ {\mathbf{H}_{4}}$,&nbsp; and agree with the given sequences.
  
−
'''2.''' Entsprechend den Gleichungen im Angabenteil gilt:
 
−
{\it \varphi}_{12}(\lambda = 0) = \frac{1}{4} \cdot \left [ (+1) \cdot (+1) + (-1) \cdot (+1) + (+1) \cdot (-1) + (-1) \cdot (-1) \right ] = 0\hspace{0.05cm},
 
−
{\it \varphi}_{13}(\lambda = 0) = \frac{1}{4} \cdot \left [ (+1) \cdot (+1) + (-1) \cdot (-1) + (+1) \cdot (-1) + (-1) \cdot (+1) \right ] = 0\hspace{0.05cm},
 
−
{\it \varphi}_{23}(\lambda = 0) = \frac{1}{4} \cdot \left [ (+1) \cdot (+1) + (+1) \cdot (-1) + (-1) \cdot (-1) + (-1) \cdot (+1) \right ] = 0\hspace{0.05cm}.
 
−
Auch für größere Werte von J ist der PKKF–Wert φ_{ij}(λ = 0) für i ≠ j stets 0. Daraus folgt: Bei synchronem CDMA stören sich die Teilnehmer nicht. Richtig sind somit alle Aussagen mit Ausnahme von Lösungsvorschlag (4).
 
  
−
'''3.''' Die PKKF φ_{12}(λ) ist für alle Werte von λ gleich 0, wie die folgenden Zeilen zeigen:
+
'''(2)'''&nbsp; <u>Solutions 1, 2 and 3</u>&nbsp; are correct:
−
$$\langle w_\nu^{(1)}\rangle  = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \langle w_\nu^{(2)}\rangle  =  {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},$$  
+
*According to the equations in the data section,&nbsp; the following holds:
−
$$\langle w_{\nu+1}^{(2)}\rangle  = {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},$$
+
:$${\it \varphi}_{12}(\lambda = 0) = 1/4 \cdot \left [ (+1) \cdot (+1) + (-1) \cdot (+1) + (+1) \cdot (-1) + (-1) \cdot (-1) \right ] = 0\hspace{0.05cm},$$  
−
$$\langle w_{\nu+2}^{(2)}\rangle  =  {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$  
+
:$${\it \varphi}_{13}(\lambda = 0) = 1/4\cdot \left [ (+1) \cdot (+1) + (-1) \cdot (-1) + (+1) \cdot (-1) + (-1) \cdot (+1) \right ] = 0\hspace{0.05cm},$$  
−
$$\langle w_{\nu+3}^{(2)}\rangle  = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm}{\rm Produkt\hspace{0.1cm} mit \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$
+
:$${\it \varphi}_{23}(\lambda = 0) =1/4 \cdot \left [ (+1) \cdot (+1) + (+1) \cdot (-1) + (-1) \cdot (-1) + (-1) \cdot (+1) \right ] = 0\hspace{0.05cm}.$$
−
$$\langle w_{\nu+4}^{(2)}\rangle  =  {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} = \langle w_\nu^{(2)}\rangle \hspace{0.05cm}.$$
+
*Also,&nbsp; for larger values of&nbsp; $J$,&nbsp; for&nbsp; $i ≠ j$&nbsp; the PCCF value is always&nbsp; $φ_{ij}(λ = 0)= 0$.  
−
Das gleiche gilt für die PKKF $φ_{13}(λ)$. Dagegen erhält man für die PKKF zwischen den Folgen 〈$w_ν^{(2)}$〉 und 〈$w_ν{(3)}$〉:
+
*It follows: &nbsp; In synchronous CDMA,&nbsp; the subscribers do not interfere with each other.
−
$${\it \varphi}_{23}(\lambda ) = \left\{ \begin{array}{c}0 \\+1\\ -1 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c} \lambda = 0, \pm 2, \pm 4,\pm 6, ... \hspace{0.05cm}, \\ \hspace{0.14cm} \lambda = ... \hspace{0.05cm} , -3, +1, +5, ... \hspace{0.05cm}, \\ \hspace{0.14cm} \lambda = ... \hspace{0.05cm} , -5, -1, +3, ... \hspace{0.05cm}. \\ \end{array}$$
 
  
−
Das bedeutet: Wird das Signal von Teilnehmer 3 gegenüber Teilnehmer 2 um ein Spreizchip verzögert oder umgekehrt, so lassen sich die Teilnehmer nicht mehr trennen und es kommt zu einer signifikanten Erhöhung der Fehlerwahrscheinlichkeit. Richtig sind also nur die Lösungsvorschläge 1 und 2.
 
  
−
In der nachfolgenden Grafik sind die PKKF–Kurven gestrichelt eingezeichnet (violett und rot).
 
  
−
[[File:P_ID1890__Mod_A_5_4c.png]]
+
'''(3)'''&nbsp; <u>Solutions 1 and 2</u>&nbsp; are correct:
 +
*For all values of&nbsp; λ,&nbsp; the PCCF is&nbsp; φ_{12}(λ) = 0,&nbsp; as shown by the following lines:
 +
:\langle w_\nu^{(1)}\rangle  =  {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \langle w_\nu^{(2)}\rangle  =  {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \hspace{0.3cm}{\rm product\hspace{0.1cm} with \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},
 +
:\langle w_{\nu+1}^{(2)}\rangle  =  {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \hspace{0.3cm}{\rm product\hspace{0.1cm} with \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},
 +
:\langle w_{\nu+2}^{(2)}\rangle  =  {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm}{\rm product\hspace{0.1cm} with \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},
 +
:\langle w_{\nu+3}^{(2)}\rangle  =  {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm}{\rm product\hspace{0.1cm} with \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},
 +
:\langle w_{\nu+4}^{(2)}\rangle  =  {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} = \langle w_\nu^{(2)}\rangle \hspace{0.05cm}.
 +
[[File:P_ID1890__Mod_A_5_4c.png|right|frame|Some PCCF and PACF curves]]
 +
*The same is true for the PCCF&nbsp; φ_{13}(λ).
 +
*In contrast,&nbsp; for the PCCF between the sequences&nbsp; \langle w_\nu^{(2)}\rangle&nbsp; and&nbsp; \langle w_\nu^{(3)}\rangle&nbsp; we obtain:
  
 +
:{\it \varphi}_{23}(\lambda ) = \left\{ \begin{array}{c}0 \\+1\\ -1 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array} \begin{array}{*{20}c} \lambda = 0, \pm 2, \pm 4,\pm 6, ... \hspace{0.05cm}, \\ \hspace{0.14cm} \lambda = ... \hspace{0.05cm} , -3, +1, +5, ... \hspace{0.05cm}, \\ \hspace{0.14cm} \lambda = ... \hspace{0.05cm} , -5, -1, +3, ... \hspace{0.05cm}. \\ \end{array}
 +
*This means: &nbsp; If the signal from subscriber&nbsp; 3&nbsp; is delayed by one spreading chip with respect to subscriber&nbsp; 2&nbsp; or vice versa,&nbsp; the subscribers can no longer be separated and there is a significant increase in the error probability.
 +
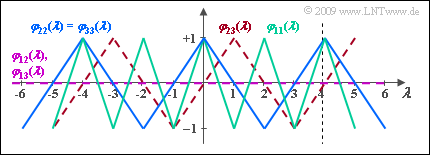
*In the diagram,&nbsp; the PCCF curves are drawn in dashed lines&nbsp; (violet and red).
  
−
'''4.'''  Richtig sind die Aussagen 1, 2 und 4. Da die Walsh–Funktion Nr. 1 periodisch ist mit T_0 = 2T_c, ist auch die PAKF periodisch mit λ = 2.
 
  
−
Die zweite Aussage ist richtig, wie die folgende Rechnung zeigt (grüner Kurvenzug):
 
−
{\it \varphi}_{11}(\lambda = 0)  =  \frac{1}{4} \cdot \left [ (+1) \cdot (+1) + (-1) \cdot (-1) + (+1) \cdot (+1) + (-1) \cdot (-1) \right ] = 1\hspace{0.05cm},
 
−
{\it \varphi}_{11}(\lambda = 1)  =  \frac{1}{4} \cdot \left [ (+1) \cdot (-1) + (+1) \cdot (-1) + (+1) \cdot (-1) + (+1) \cdot (-1) \right ] = -1\hspace{0.05cm}.
 
−
Da sich die beiden Walsh–Funktionen Nr. 2 und 3 nur durch eine Verschiebung um T_c unterscheiden und sich eine Phase in der PAKF prinzipiell nicht auswirkt, ist tatsächlich entsprechend dem letzten Lösungsvorschlag φ_{33}(λ) = φ_{22}(λ). Diese beiden PAKF–Funktionen sind blau eingezeichnet.
 
  
−
Dagegen unterscheidet sich φ_{22}(λ) von φ_{11}(λ) durch eine andere Periodizität: φ_{22}(λ) = φ_{33}(λ) ist doppelt so breit wie φ_{11}(λ).
+
'''(4)'''&nbsp; <u>Statements 1,&nbsp; 2&nbsp; and 4</u>&nbsp; are correct:
 +
* Since the Walsh function no.&nbsp; 1&nbsp; is periodic with&nbsp; T_0 = 2T_c,&nbsp; the PACF is also periodic with&nbsp; λ = 2.
 +
*The second statement is correct,&nbsp; as shown by the following calculation&nbsp; (green curve):
 +
:{\it \varphi}_{11}(\lambda = 0)  =  1/4 \cdot \big [ (+1) \cdot (+1) + (-1) \cdot (-1) + (+1) \cdot (+1) + (-1) \cdot (-1) \big ] = +1\hspace{0.05cm},
 +
:{\it \varphi}_{11}(\lambda = 1)  =  1/4 \cdot \big [ (+1) \cdot (-1) + (+1) \cdot (-1) + (+1) \cdot (-1) + (+1) \cdot (-1) \big ] = -1\hspace{0.05cm}.
 +
*Since the two Walsh functions no.&nbsp; 2&nbsp; and&nbsp; 3&nbsp; differ only by a shift around&nbsp; T_c&nbsp; and a phase in the PACF has no effect in principle,&nbsp; in fact,&nbsp; according to the last statement,&nbsp; φ_{33}(λ) = φ_{22}(λ).&nbsp; These two PACF functions are plotted in blue.
 +
*In contrast,&nbsp; φ_{22}(λ)&nbsp; differs from&nbsp; φ_{11}(λ)&nbsp; by a different periodicity: &nbsp; φ_{22}(λ) = φ_{33}(λ)&nbsp; is twice as wide as&nbsp; φ_{11}(λ).
  
 
{{ML-Fuß}}
 
{{ML-Fuß}}
Line 99: Line 113:
  
  
−
[[Category:Aufgaben zu Modulationsverfahren|^5.3 Spreizfolgen für CDMA^]]
+
[[Category:Modulation Methods: Exercises|^5.3 Spread Sequences for CDMA^]]

Latest revision as of 16:31, 13 December 2021

Hadamard matrix  {\mathbf{H}_{8}}

The so-called  "Walsh functions",  which can be constructed by means of the Hadamard matrix,  are often used for band spreading and band compression.  Starting from the matrix

{\mathbf{H}_{2}} = \left[ \begin{array}{ccc} +1 & +1 \\ +1 & -1 \end{array} \right]

the further Hadamard matrices   {\mathbf{H}_{4}},   {\mathbf{H}_{8}},  etc. can be derived by the following recursion:

{\mathbf{H}_{2J}} = \left[ \begin{array}{ccc} \mathbf{H}_J & \mathbf{H}_J \\ \mathbf{H}_J & -\mathbf{H}_J \end{array} \right] \hspace{0.05cm}.

The diagram shows the matrix   {\mathbf{H}_{8}}  for the spreading factor  J = 8.  From this we can derive the spreading sequences

\langle w_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},
\langle w_\nu^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},
...
\langle w_\nu^{(7)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm}{+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}

for seven CDMA subscribers.  The spreading sequence   \langle w_\nu^{(0)}\rangle  corresponding to the first row in the Hadamard matrix is usually not assigned because it does not spread.

The questions mostly refer to the spreading factor  J = 4.  Thus,  correspondingly,  a maximum of three CDMA subscribers can be supplied with the spreading sequences   \langle w_\nu^{(1)}\rangle,   \langle w_\nu^{(2)}\rangle  and   \langle w_\nu^{(3)}\rangle,  which result from the second, third and fourth rows of the matrix {\mathbf{H}_{4}}.

Regarding the correlation functions, the following nomenclature shall apply in this exercise:

  • The  periodic cross-correlation function  \rm (PCCF)  between the sequences   \langle w_\nu^{(i)}\rangle  and   \langle w_\nu^{(j)}\rangle  is denoted by  φ_{ij}(λ).   Here:
{\it \varphi}_{ij}(\lambda) = {\rm E}\left [ w_{\nu}^{(i)} \cdot w_{\nu+ \lambda}^{(j)} \right ] \hspace{0.05cm}.
  • If  φ_{ij} \equiv 0  (that is:  φ_{ij}(λ) = 0  for all values of  λ),  the CDMA subscribers do not interfere with each other,  even if they have different propagation times.
  • If at least  φ_{ij}({\it λ} = 0) = 0  applies,  then no interference occurs,  at least in synchronous CDMA operation  (no or equal propagation times of all subscribers). 
  • The  periodic auto-correlation function  \rm (PACF)  of the Walsh function   \langle w_\nu^{(i)}\rangle  is denoted by  φ_{ii}(λ),  and it holds:
{\it \varphi}_{ii}(\lambda) = {\rm E}\left [ w_{\nu}^{(i)} \cdot w_{\nu+ \lambda}^{(i)} \right ] \hspace{0.05cm}.


Notes:

  • The exercise belongs to the chapter  Spreading Sequences for CDMA.
  • Reference is made in particular to the section  Walsh functions  in the theory part.
  • We would also like to draw your attention to the interactive applet  Generation of Walsh functions. 
  • The abscissa is normalized to the chip duration  T_c.  This means that  λ = 1  actually describes a shift by the delay time  τ = T_c. 


Questions

1

What are the spreading sequences for  J = 4?

\langle w_\nu^{(1)}\rangle = +\hspace{-0.05cm}1 -\hspace{-0.15cm}1 +\hspace{-0.15cm}1 -\hspace{-0.15cm}1,
\langle w_\nu^{(2)}\rangle = +\hspace{-0.05cm}1 +\hspace{-0.15cm}1 -\hspace{-0.15cm}1 -\hspace{-0.15cm}1,
\langle w_\nu^{(3)}\rangle = +\hspace{-0.05cm}1 -\hspace{-0.15cm}1 -\hspace{-0.15cm}1 +\hspace{-0.15cm}1.

2

Which statements are true regarding the PCCF values  φ_{ij}(λ = 0)?

For J = 4,   φ_{12}(λ = 0) = 0.
For J = 4,   φ_{13}(λ = 0) = 0.
For J = 4,   φ_{23}(λ = 0) = 0.
For J = 8,   φ_{ij}(λ = 0) ≠ 0  may well hold  (i ≠ j).
In synchronous CDMA,  the subscribers do not interfere with each other.

3

Which statements are true for the PCCF values with  λ ≠ 0?

For all values of  λ,  the PCCF is  φ_{12}(λ) = 0.
For all values of  λ,  the PCCF is  φ_{13}(λ) = 0.
For all values of  λ,  the PCCF is  φ_{23}(λ) = 0.
In asynchronous CDMA,  the subscribers do not interfere with each other.

4

Which statements are true for the PACF curves?

All   φ_{ii}(λ)  curves are periodic.
 φ_{11}(λ = 0) = +\hspace{-0.05cm}1  and  φ_{11}(λ = 1) = -\hspace{-0.05cm}1  hold.
 φ_{22}(λ) = φ_{11}(λ)  holds.
 φ_{33}(λ) = φ_{22}(λ)  holds.


Solution

Solution

(1)  All solutions  are correct:

  • The matrix  {\mathbf{H}_{4}}  is the upper left submatrix of  {\mathbf{H}_{8}}.
  • The spreading sequences result from the rows 2,  3  and 4  of  {\mathbf{H}_{4}},  and agree with the given sequences.


(2)  Solutions 1, 2 and 3  are correct:

  • According to the equations in the data section,  the following holds:
{\it \varphi}_{12}(\lambda = 0) = 1/4 \cdot \left [ (+1) \cdot (+1) + (-1) \cdot (+1) + (+1) \cdot (-1) + (-1) \cdot (-1) \right ] = 0\hspace{0.05cm},
{\it \varphi}_{13}(\lambda = 0) = 1/4\cdot \left [ (+1) \cdot (+1) + (-1) \cdot (-1) + (+1) \cdot (-1) + (-1) \cdot (+1) \right ] = 0\hspace{0.05cm},
{\it \varphi}_{23}(\lambda = 0) =1/4 \cdot \left [ (+1) \cdot (+1) + (+1) \cdot (-1) + (-1) \cdot (-1) + (-1) \cdot (+1) \right ] = 0\hspace{0.05cm}.
  • Also,  for larger values of  J,  for  i ≠ j  the PCCF value is always  φ_{ij}(λ = 0)= 0.
  • It follows:   In synchronous CDMA,  the subscribers do not interfere with each other.


(3)  Solutions 1 and 2  are correct:

  • For all values of  λ,  the PCCF is  φ_{12}(λ) = 0,  as shown by the following lines:
\langle w_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \langle w_\nu^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \hspace{0.3cm}{\rm product\hspace{0.1cm} with \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},
\langle w_{\nu+1}^{(2)}\rangle = {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm}, \hspace{0.3cm}{\rm product\hspace{0.1cm} with \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},
\langle w_{\nu+2}^{(2)}\rangle = {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm}{\rm product\hspace{0.1cm} with \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},
\langle w_{\nu+3}^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm}{\rm product\hspace{0.1cm} with \hspace{0.1cm}}\langle w_\nu^{(1)}\rangle: {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},
\langle w_{\nu+4}^{(2)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} = \langle w_\nu^{(2)}\rangle \hspace{0.05cm}.
Some PCCF and PACF curves
  • The same is true for the PCCF  φ_{13}(λ).
  • In contrast,  for the PCCF between the sequences  \langle w_\nu^{(2)}\rangle  and  \langle w_\nu^{(3)}\rangle  we obtain:
{\it \varphi}_{23}(\lambda ) = \left\{ \begin{array}{c}0 \\+1\\ -1 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array} \begin{array}{*{20}c} \lambda = 0, \pm 2, \pm 4,\pm 6, ... \hspace{0.05cm}, \\ \hspace{0.14cm} \lambda = ... \hspace{0.05cm} , -3, +1, +5, ... \hspace{0.05cm}, \\ \hspace{0.14cm} \lambda = ... \hspace{0.05cm} , -5, -1, +3, ... \hspace{0.05cm}. \\ \end{array}
  • This means:   If the signal from subscriber  3  is delayed by one spreading chip with respect to subscriber  2  or vice versa,  the subscribers can no longer be separated and there is a significant increase in the error probability.
  • In the diagram,  the PCCF curves are drawn in dashed lines  (violet and red).


(4)  Statements 1,  2  and 4  are correct:

  • Since the Walsh function no.  1  is periodic with  T_0 = 2T_c,  the PACF is also periodic with  λ = 2.
  • The second statement is correct,  as shown by the following calculation  (green curve):
{\it \varphi}_{11}(\lambda = 0) = 1/4 \cdot \big [ (+1) \cdot (+1) + (-1) \cdot (-1) + (+1) \cdot (+1) + (-1) \cdot (-1) \big ] = +1\hspace{0.05cm},
{\it \varphi}_{11}(\lambda = 1) = 1/4 \cdot \big [ (+1) \cdot (-1) + (+1) \cdot (-1) + (+1) \cdot (-1) + (+1) \cdot (-1) \big ] = -1\hspace{0.05cm}.
  • Since the two Walsh functions no.  2  and  3  differ only by a shift around  T_c  and a phase in the PACF has no effect in principle,  in fact,  according to the last statement,  φ_{33}(λ) = φ_{22}(λ).  These two PACF functions are plotted in blue.
  • In contrast,  φ_{22}(λ)  differs from  φ_{11}(λ)  by a different periodicity:   φ_{22}(λ) = φ_{33}(λ)  is twice as wide as  φ_{11}(λ).

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_5.4:_Walsh_Functions_(PCCF,_PACF)&oldid=43816"
  • Powered by MediaWiki