Difference between revisions of "Channel Coding/Decoding of Linear Block Codes"
| (63 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Binary Block Codes for Channel Coding |
| − | |Vorherige Seite= | + | |Vorherige Seite=General Description of Linear Block Codes |
| − | |Nächste Seite= | + | |Nächste Seite=Limits for Block Error Probability |
}} | }} | ||
| − | == | + | == Block diagram and requirements == |
<br> | <br> | ||
| − | + | We start from the block diagram already shown in the chapter [[Channel_Coding/Channel_Models_and_Decision_Structures|$\text{Channel Models and Decision Structures}$]] where the digital channel model used is mostly the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|$\text{Binary Symmetric Channel}$]] $\rm (BSC)$. | |
| − | [[ | + | For code word estimation, we use the "Maximum Likelihood Decision" $\rm (ML)$, which for binary codes ⇒ $\underline{x} \in {\rm GF}(2^n)$ at the block level gives the same result as the [[Channel_Coding/Channel_Models_and_Decision_Structures#Definitions_of_the_different_optimal_receivers|$\text{MAP Receiver}$]].<br> |
| − | + | [[File:EN_KC_T_1_5_S1.png|right|frame|Block diagram for decoding block codes|class=fit]] | |
| − | |||
| − | : | + | The task of the channel decoder can be described as follows: |
| + | *The vector $\underline{v}$ after decoding (at the sink) should match the information word $\underline{u}$ as well as possible. | ||
| − | * | + | *That is: The »'''block error probability'''« should be as small as possible: |
| + | ::<math>{ \rm Pr(block\:error)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm minimum}\hspace{0.05cm}.</math> | ||
| − | + | *Because of assignments $\underline{x} = {\rm enc}(\underline{u})$ resp. $\underline{v} = {\rm enc}^{-1}(\underline{z})$ also holds: | |
| − | + | ::<math>{ \rm Pr(block\:error)} = { \rm Pr}( \underline{z} \ne \underline{x}) \stackrel{!}{=} { \rm minimum}\hspace{0.05cm}.</math> | |
| + | *Sought is the most likely sent code word $\underline{y} = \underline{x} +\underline{e}$ for the given received word $\underline{x}_i$, which is passed on as result $\underline{z}$: | ||
::<math>\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.</math> | ::<math>\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.</math> | ||
| − | * | + | *For the BSC model, both $\underline{x}_i \in {\rm GF}(2^n)$ and $\underline{y} \in {\rm GF}(2^n)$, so the maximum likelihood decision rule can also be written using the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding |$\text{Hamming distance}$]] $d_{\rm H}( \underline{y}, \, \underline{x}_i)$: |
::<math>\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ::<math>\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ||
d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | ||
| − | == | + | == Principle of syndrome decoding == |
<br> | <br> | ||
| − | + | Assumed here is a $(n, \, k)$ block code with the parity-check matrix $\boldsymbol{\rm H}$ and the systematic code words | |
| − | ::<math>\underline{x}\hspace{0.05cm} = (x_1, x_2, ... \hspace{0.05cm}, x_i, ... \hspace{0.05cm}, x_n) | + | ::<math>\underline{x}\hspace{0.05cm} = (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) |
| − | = (u_1, u_2, ... \hspace{0.05cm}, u_k, p_1, ... \hspace{0.05cm}, p_{n-k})\hspace{0.05cm}. </math> | + | = (u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k, p_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, p_{n-k})\hspace{0.05cm}. </math> |
| − | + | With the error vector $\underline{e}$ then applies to the received word: | |
| − | ::<math>\underline{y} = \underline{x} + \underline{e} \hspace{0.05cm}, \hspace{0.4cm} \underline{y} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0. | + | ::<math>\underline{y} = \underline{x} + \underline{e} \hspace{0.05cm}, \hspace{0.4cm} \underline{y} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{x} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{e} \in \hspace{0.1cm} {\rm GF}(2^n) |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | A bit error at position $i$ ⇒ $y_i ≠ x_i$ is expressed by the »'''error coefficient'''« $e_i = 1$.<br> | |
| − | {{Definition} | + | {{BlaueBox|TEXT= |
| + | $\text{Definition:}$ The »'''syndrome'''« $\underline{s} = (s_0, s_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, s_{m-1})$ is calculated (as row resp. column vector) from the received word $\underline{y}$ and the parity-check matrix $\boldsymbol{\rm H}$ as follows: | ||
| − | :<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T}\hspace{0.3cm}{\rm bzw.}\hspace{0.3cm} | + | ::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T}\hspace{0.3cm}{\rm bzw.}\hspace{0.3cm} |
| − | \underline{s}^{\rm T} = { \boldsymbol{\rm H}} \cdot \underline{y}^{\rm T}\hspace{0.05cm}.</math> | + | \underline{s}^{\rm T} = { \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T}\hspace{0.05cm}.</math> |
| − | + | *The vector length of $\underline{s}$ is equal to $m = n-k$ $($row number of $\boldsymbol{\rm H})$.}}<br> | |
| − | + | The syndrome $\underline{s}$ shows the following characteristics: | |
| − | * | + | *Because of the equation $\underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{0}$ the syndrome $\underline{s}$ does not depend on the code word $\underline{x}$ but solely on the error vector $\underline{e}$: |
::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} | ::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} | ||
| Line 59: | Line 62: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *For sufficiently few bit errors, $\underline{s}$ provides a clear indication of the error locations, allowing full error correction.<br><br> |
| − | {{ | + | {{GraueBox|TEXT= |
| + | $\text{Example 1:}$ Starting from the systematic [[Channel_Coding/General_Description_of_Linear_Block_Codes#Some_properties_of_the_.287.2C_4.2C_3.29_Hamming_code|$\text{(7, 4, 3)}$ Hamming code]], the following result is obtained for the received vector $\underline{y} = (0, 1, 1, 1, 0, 0, 1)$: | ||
| − | :<math>{ \boldsymbol{\rm H}} \cdot \underline{y}^{\rm T} | + | ::<math>{ \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T} |
= \begin{pmatrix} | = \begin{pmatrix} | ||
1 &1 &1 &0 &1 &0 &0\\ | 1 &1 &1 &0 &1 &0 &0\\ | ||
| Line 82: | Line 86: | ||
\end{pmatrix} = \underline{s}^{\rm T} \hspace{0.05cm}.</math> | \end{pmatrix} = \underline{s}^{\rm T} \hspace{0.05cm}.</math> | ||
| − | + | Comparing the syndrome with the [[Channel_Coding/General_Description_of_Linear_Block_Codes#Code_definition_by_the_parity-check_matrix|$\text{parity-check equations}$]] of the Hamming code, we see that | |
| − | * | + | *most likely the fourth symbol $(x_4 = u_4)$ of the code word has been falsified,<br> |
| − | * | + | *the code word estimator will thus yield the result $\underline{z} = (0, 1, 1, 0, 0, 0, 1)$,<br> |
| − | * | + | *the decision is correct only if only one bit was falsified during transmission.<br><br> |
| − | + | Below are the required corrections for the $\text{(7, 4, 3)}$ Hamming code resulting from the calculated syndrome $\underline{s}$ corresponding to the columns of the parity-check matrix: | |
| − | :<math>\underline{s | + | ::<math>\underline{s} = (0, 0, 0) \hspace{0.10cm} \Rightarrow\hspace{0.10cm}{\rm no\hspace{0.15cm} correction}\hspace{0.05cm};\hspace{0.8cm}\underline{s} = (1, 0, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm}{\rm invert}\hspace{0.15cm}p_1\hspace{0.05cm};</math> |
| − | :<math>\underline{s | + | ::<math>\underline{s} =(0, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}p_3\hspace{0.05cm};\hspace{1.63cm}\underline{s} = (1, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}u_1\hspace{0.05cm};</math> |
| − | :<math>\underline{s | + | ::<math>\underline{s} =(0, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}p_2\hspace{0.05cm};\hspace{1.63cm}\underline{s} = (1, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}u_3\hspace{0.05cm};</math> |
| − | :<math>\underline{s | + | ::<math>\underline{s} =(0, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}u_4\hspace{0.05cm};\hspace{1.63cm}\underline{s} = (1, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}u_2\hspace{0.05cm}. </math>}}<br> |
| − | == | + | == Generalization of syndrome coding == |
<br> | <br> | ||
| − | + | We continue to assume the BSC channel model. This means: | |
| + | *The received vector $\underline{y}$ and the error vector $\underline{e}$ are elements of ${\rm GF}(2^n)$. | ||
| + | |||
| + | *The possible code words $\underline{x}_i$ belong to the code $\mathcal{C}$, which spans a $(n-k)$-dimensional subspace of ${\rm GF}(2^n)$. | ||
| − | * | + | |
| + | Under this assumption, we briefly summarize the results of the last sections: | ||
| + | *Syndrome decoding is a realization possibility of maximum likelihood decoding of block codes. One decides on the code word $\underline{x}_i$ with the least Hamming distance to the received word $\underline{y}$: | ||
::<math>\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ::<math>\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ||
d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | ||
| − | * | + | *But the syndrome decoding is also the search for the most probable error vector $\underline{e}$ that satisfies the condition $\underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{s}$. The "syndrome" is thereby determined by the equation |
| + | :$$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} .$$ | ||
| − | * | + | *With the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|$\text{Hamming weight}$]] $w_{\rm H}(\underline{e})$ the second interpretation can also be mathematically formulated as follows: |
::<math>\underline{z} = \underline{y} + {\rm arg} \min_{\underline{e}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} {\rm GF}(2^n)} \hspace{0.1cm} | ::<math>\underline{z} = \underline{y} + {\rm arg} \min_{\underline{e}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} {\rm GF}(2^n)} \hspace{0.1cm} | ||
w_{\rm H}(\underline{e}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | w_{\rm H}(\underline{e}_{\hspace{0.03cm}i})\hspace{0.05cm}.</math> | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Conclusion:}$ Note that the error vector $\underline{e}$ as well as the received vector $\underline{y}$ is an element of ${\rm GF}(2^n)$ unlike the syndrome $\underline{s} \in {\rm GF}(2^m)$ with number $m = n-k$ of parity-check equations. This means, that | |
| + | *the association between the syndrome $\underline{s}$ and the error vector $\underline{e}$ is not unique, but | ||
| − | * | + | *each $2^k$ error vectors lead to the same syndrome $\underline{s}$ which one groups together into a so-called "coset".}}<br> |
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Example 2:}$ The facts shall be illustrated by the example with parameters $n = 5, \ k = 2$ ⇒ $m = n-k = 3$ . | |
| − | + | [[File:EN_KC_T_1_5_S3a.png|right|frame|Splitting the $2^k$ error vectors into "cosets"|class=fit]] | |
| − | + | You can see from this graph: | |
| − | == | + | #The $2^n = 32$ possible error vectors $\underline{e}$ are divided into $2^m = 8$ cosets ${\it \Psi}_0$, ... , ${\it \Psi}_7$. Explicitly drawn here are only the cosets ${\it \Psi}_0$ and ${\it \Psi}_5$.<br><br> |
| − | <br> | + | #All $2^k = 4$ error vectors of the coset ${\it \Psi}_\mu$ lead to the syndrome $\underline{s}_\mu$.<br><br> |
| − | + | #Each minor class ${\it \Psi}_\mu$ has a "leader" $\underline{e}_\mu$, namely the one with the minimum Hamming weight.}}<br> | |
| − | : | + | {{GraueBox|TEXT= |
| + | $\text{Example 3:}$ Starting from the systematic $\text{(5, 2, 3)}$ code $\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \big \}$ the syndrome decoding procedure is now described in detail. | ||
| + | [[File:EN_KC_T_1_5_S3b_neu2.png|right|frame|Example $\text{(5, 2, 3)}$ syndrome table with cosets|class=fit]] | ||
| + | *The generator matrix and the parity-check matrix are: | ||
| − | + | ::<math>{ \boldsymbol{\rm G} } | |
| − | |||
| − | :<math>{ \boldsymbol{\rm G}} | ||
= \begin{pmatrix} | = \begin{pmatrix} | ||
1 &0 &1 &1 &0 \\ | 1 &0 &1 &1 &0 \\ | ||
0 &1 &0 &1 &1 | 0 &1 &0 &1 &1 | ||
| − | \end{pmatrix} \hspace{0.05cm}, | + | \end{pmatrix} \hspace{0.05cm},</math> |
| + | ::<math>{ \boldsymbol{\rm H} } | ||
= \begin{pmatrix} | = \begin{pmatrix} | ||
1 &0 &1 &0 &0 \\ | 1 &0 &1 &0 &0 \\ | ||
| Line 144: | Line 156: | ||
\end{pmatrix} \hspace{0.05cm}.</math> | \end{pmatrix} \hspace{0.05cm}.</math> | ||
| − | + | *The table summarizes the final result. Note: | |
| + | #The index $\mu$ is not identical to the binary value of $\underline{s}_\mu$. | ||
| + | #The order is rather given by the number of ones in the minor class leader $\underline{e}_\mu$. | ||
| + | #For example, the syndrome $\underline{s}_5 = (1, 1, 0)$ and the syndrome $\underline{s}_6 = (1, 0, 1)$.<br> | ||
| + | |||
| + | |||
| + | *To derive this table, note: | ||
| + | #The row 1 refers to the syndrome $\underline{s}_0 = (0, 0, 0)$ and the associated cosets ${\it \Psi}_0$. The most likely error sequence here is $(0, 0, 0, 0, 0)$ ⇒ no bit error, which we call the "coset leader" $\underline{e}_0$. | ||
| + | #The other entries in the first row, namely $(1, 0, 1, 1, 0 )$, $(0, 1, 0, 1, 1)$ and $(1, 1, 1, 0, 1 )$, also each yield the syndrome $\underline{s}_0 = (0, 0, 0)$, but only result with at least three bit errors and are correspondingly unlikely.<br> | ||
| + | #In rows 2 to 6, the respective coset leader $\underline{e}_\mu$ contains exactly a single "$1$" $(\mu = 1$, ... , $5)$. Here $\underline{e}_\mu$ is always the most likely error pattern of the class ${\it \Psi}_\mu$. The other group members result only with at least two bit errors.<br> | ||
| + | #The syndrome $\underline{s}_6 = (1, 0, 1)$ is not possible with only one bit error. In creating the table, we then considered all "$5\text{ over }2 = 10$" error patterns $\underline{e}$ with weight $w_{\rm H}(\underline{e}) = 2$. | ||
| + | #The first found sequence with syndrome $\underline{s}_6 = (1, 0, 1)$ was chosen as coset leader $\underline{e}_6 = (1, 1, 0, 0)$ . With a different probing order, the sequence $(0, 0, 1, 0, 1)$ could also have resulted from ${\it \Psi}_6$.<br> | ||
| + | #Similar procedure was followed in determining the leader $\underline{e}_7 = (0, 1, 1, 0, 0)$ of the cosets class ${\it \Psi}_7$ characterized by the uniform syndrome $\underline{s}_7 = (1, 1, 1)$. Also in the class ${\it \Psi}_7$ there is another sequence with Hamming weight $w_{\rm H}(\underline{e}) = 2$, namely $(1, 0, 0, 0, 1)$.<br><br> | ||
| + | |||
| + | *The table only needs to be created once. First, the syndrome must be determined, e.g. for the received vector $\underline{y} = (0, 1, 0, 0, 1)$: | ||
| + | ::<math>\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T} = \begin{pmatrix} | ||
| + | 0 &1 &0 &0 &1 | ||
| + | \end{pmatrix} \cdot | ||
| + | \begin{pmatrix} | ||
| + | 1 &1 &0 \\ | ||
| + | 0 &1 &1 \\ | ||
| + | 1 &0 &0 \\ | ||
| + | 0 &1 &0 \\ | ||
| + | 0 &0 &1 \\ | ||
| + | \end{pmatrix} = \begin{pmatrix} | ||
| + | 0 &1 &0 | ||
| + | \end{pmatrix}= \underline{s}_2 | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Using the coset leader $\underline{e}_2 = (0, 0, 0, 1, 0)$ from the above table $($red entry for $\mu =2)$ finally arrives at the decoding result: | ||
| + | |||
| + | ::<math>\underline{z} = \underline{y} + \underline{e}_2 = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1) + (0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0) = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1) | ||
| + | \hspace{0.05cm}.</math>}} | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Conclusion:}$ From these examples it is already clear that the »'''syndrome decoding means a considerable effort'''«, if one cannot use certain properties e.g. cyclic codes. | ||
| + | |||
| + | *For large block code lengths, this method fails completely. Thus, to decode a [https://en.wikipedia.org/wiki/BCH_code $\text{BCH code}$] $($the abbreviation stands for their inventors '''B'''ose, '''C'''haudhuri, '''H'''ocquenghem$)$ with code parameters $n = 511$, $k = 259$ and $d_{\rm min} = 61$, one has to evaluate and store exactly $2^{511-259} \approx 10^{76}$ error patterns of length $511$. | ||
| + | *Happily, however, there are special decoding algorithms for these and also for other codes of large block length, which lead to success with less effort}}. | ||
| + | |||
| + | == Coding gain - bit error rate with AWGN == | ||
| + | <br> | ||
| + | We now consider the [[Digital_Signal_Transmission/Error_Probability_for_Baseband_Transmission#Definition_of_the_bit_error_rate|$\text{bit error rate}$]] for the following constellation: | ||
| + | [[File:EN_KC_T_1_5_S4.png|right|frame|Bit error rate for the $\text{(7, 4, 3)}$ Hamming code|class=fit]] | ||
| + | #Hamming code $\text{HC (7, 4, 3)}$,<br> | ||
| + | #AWGN–channel, characterized by the quotient $E_{\rm B}/N_0$ (in dB),<br> | ||
| + | #Maximum Likelihood Decoder $\rm (ML)$ with <br>"Hard Decision" $\rm (HD)$ and "Soft Decision" $\rm (SD)$, resp. | ||
| + | |||
| + | |||
| + | It should be noted with regard to this graph: | ||
| + | *The black comparison curve applies e.g. to binary phase modulation $\rm (BPSK)$ without coding. For this one needs for the bit error rate $10^{-5}$ about $10 \cdot \lg \, E_{\rm B}/N_0 = 9.6 \, \rm dB$.<br> | ||
| + | |||
| + | *The red circles apply to the [[Channel_Coding/General_Description_of_Linear_Block_Codes#Some_properties_of_the_.287.2C_4.2C_3.29_Hamming_code|$\text{HC (7, 4, 3)}$]] and hard decisions of the maximum likelihood decoder $\text{(ML–HD)}$. Syndrome decoding is a possible realization form for this.<br> | ||
| + | |||
| + | *This configuration brings an improvement over the comparison system only for $10 \cdot \lg \, E_{\rm B}/N_0 >6 \, \rm dB$. For $\rm BER =10^{-5}$ one only needs $10 \cdot \lg \, E_{\rm B}/N_0 \approx 9.2 \, \rm dB$.<br> | ||
| + | |||
| + | *The green crosses for [[Channel_Coding/General_Description_of_Linear_Block_Codes#Some_properties_of_the_.287.2C_4.2C_3.29_Hamming_code|$\text{HC (7, 4, 3)}$]] and [[Channel_Coding/Soft-in_Soft-Out_Decoder| $\text{soft decision}$]] $\text{(ML–SD)}$ are below the red curve throughout the range. For $\rm BER =10^{-5}$ this gives $10 \cdot \lg \, E_{\rm B}/N_0 \approx 7.8 \, \rm dB$.<br><br> | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ We refer as »'''coding gain'''« of a considered system configuration, | ||
| + | *characterized by its code and | ||
| + | *the way it is decoded, | ||
| + | |||
| + | |||
| + | the smaller $10 \cdot \lg \, E_{\rm B}/N_0$ required for a given bit error rate $\rm (BER)$ compared to the comparison system $($without coding$)$: | ||
| + | |||
| + | ::<math>G_{\rm Code} (\hspace{0.05cm}\text{considered system} \hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm}) =10 \cdot {\rm lg}\hspace{0.1cm}{E}_{\rm B}/N_0 | ||
| + | \hspace{0.15cm}(\hspace{0.05cm}\text{comparison system}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm})- | ||
| + | 10 \cdot {\rm lg}\hspace{0.1cm}{E}_{\rm B}/N_0 | ||
| + | \hspace{0.15cm}(\hspace{0.05cm}\text{considered system}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm}) | ||
| + | \hspace{0.05cm}. </math>}}<br> | ||
| + | |||
| + | Applied to the above graph, one obtains: | ||
| + | |||
| + | :<math>G_{\rm Code} (\hspace{0.05cm}{\rm Hamming \hspace{0.1cm}(7,\hspace{0.02cm}4,\hspace{0.02cm}3), ML-HD}\hspace{0.05cm}|\hspace{0.05cm}{\rm BER} = 10^{-5}\hspace{0.05cm}) = 0.4\ {\rm dB}\hspace{0.05cm},</math> | ||
| + | |||
| + | :<math>G_{\rm Code} (\hspace{0.05cm}{\rm Hamming \hspace{0.1cm}(7,\hspace{0.02cm}4,\hspace{0.02cm}3), ML-SD}\hspace{0.05cm}|\hspace{0.05cm}{\rm BER} = 10^{-5}\hspace{0.05cm}) = 1.8\ {\rm dB}\hspace{0.05cm}.</math><br> | ||
| + | |||
| + | == Decoding at the Binary Erasure Channel == | ||
| + | <br> | ||
| + | Finally, it will be shown to what extent the decoder has to be modified | ||
| + | *if instead of the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC| $\text{BSC model}$]] ("Binary Symmetric Channel") | ||
| + | *the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Erasure_Channel_.E2.80.93_BEC|$\text{BEC model}$]] ("Binary Erasure Channel") is used, | ||
| + | |||
| + | |||
| + | which does not produce errors but marks uncertain bits as "erasures".<br> | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 4:}$ We consider again as in [[Channel_Coding/Decoding_of_Linear_Block_Codes#Generalization_of_syndrome_coding|$\text{Example 3}$]] the systematic $\text{(5, 2, 3)}$ block code | ||
| + | :$$\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.3cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.3cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.3cm}(1, 1, 1, 0, 1) \big \}.$$ | ||
| + | |||
| + | The graphic shows the system model and gives exemplary values for the individual vectors. | ||
| + | *The left part of the picture (yellow background) is valid for "BSC" with one bit error $(0 → 1)$ at the third bit. | ||
| + | *The right part of the picture (green background) is for "BEC" and shows two erasures $(\rm 1 → E)$ at the second and the fourth bit. | ||
| + | [[File:EN_KC_T_1_5_S5.png|right|frame|Error correction with BSC and BEC]] | ||
| − | |||
| − | + | One recognizes: | |
| − | * | + | *With BSC only $t = 1$ bit error (marked in red in the left part) can be corrected due to $d_{\rm min} = 3$. If one restricts oneself to error detection, this works up to $e= d_{\rm min} -1 = 2$ bit errors.<br> |
| + | |||
| + | *For BEC, error detection makes no sense, because already the channel locates an uncertain bit as an "erasure" $\rm E$. The zeros and ones in the BEC received word $\underline{y}$ are safe. Therefore the error correction works here up to $e = 2$ erasures (marked in red in the right part) with certainty.<br> | ||
| + | |||
| + | *Also $e = 3$ erasures are sometimes still correctable. So $\underline{y} \rm = (E, E, E, 1, 1)$ to $\underline{z} \rm = (0, 1, 0, 1, 1)$ to be corrected since no second code word ends with two ones. But $\underline{y} \rm = (0, E, 0, E, E)$ is not correctable because of the all zero word allowed in the code.<br> | ||
| + | |||
| + | *If it is ensured that there are no more than two erasures in any received word, the BEC block error probability ${\rm Pr}(\underline{z} \ne \underline{x}) = {\rm Pr}(\underline{v} \ne \underline{u}) \equiv 0$. In contrast, the corresponding block error probability in the BSC model always has a value greater than $0$. | ||
| + | |||
| + | |||
| + | Since after the BEC each received word is either decoded correctly or not at all, we call here the block $\underline{y} → \underline{z}$ in the future "code word finder". An "estimation" takes place only in the BSC model.<br>}}<br> | ||
| + | |||
| + | But how does the decoding of a received word $\underline{y}$ with erasures work algorithmically? | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 5:}$ Starting from the received word $\underline{y} \rm = (0, E, 0, E, 1)$ in $\text{Example 4}$ we formally set the output of the code word finder to $\underline{z} \rm = (0, z_2, 0, z_4, 1)$, where the symbols $z_2 \in \{0, \, 1\}$ and $z_4 \in \{0, \, 1\}$ are to be determined according to the following equation: | ||
| + | |||
| + | ::<math>\underline{z} \cdot { \boldsymbol{\rm H} }^{\rm T}= \underline{0} | ||
| + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| + | { \boldsymbol{\rm H} } \cdot \underline{z}^{\rm T}= \underline{0}^{\rm T} \hspace{0.05cm}.</math> | ||
| + | |||
| + | The task is now to implement this determination equation as efficiently as possible. The following calculation steps result: | ||
| + | *With the parity-check matrix $\boldsymbol{\rm H}$ of the $\text{(5, 2, 3)}$ block code and the vector $\underline{z} \rm = (0, z_2, 0, z_4, 1)$ is the above determination equation: | ||
| + | |||
| + | ::<math>{ \boldsymbol{\rm H} } \cdot \underline{z}^{\rm T} | ||
| + | = \begin{pmatrix} | ||
| + | 1 &0 &1 &0 &0\\ | ||
| + | 1 &1 &0 &1 &0\\ | ||
| + | 0 &1 &0 &0 &1 | ||
| + | \end{pmatrix} \cdot \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | z_2 \\ | ||
| + | 0 \\ | ||
| + | z_4 \\ | ||
| + | 1 | ||
| + | \end{pmatrix} = \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | 0 | ||
| + | \end{pmatrix} | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | *We sum up the "correct bits" (German: "korrekt" ⇒ subscript "K") to the vector $\underline{z}_{\rm K}$ and the "erased bits" to the vector $\underline{z}_{\rm E}$. Then we split the parity-check matrix $\boldsymbol{\rm H}$ into the corresponding submatrices $\boldsymbol{\rm H}_{\rm K}$ and $\boldsymbol{\rm H}_{\rm E}$: | ||
| + | |||
| + | ::<math>\underline{z}_{\rm K} =(0, 0, 1)\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm H} }_{\rm K}= | ||
| + | \begin{pmatrix} | ||
| + | 1 &1 &0\\ | ||
| + | 1 &0 &0\\ | ||
| + | 0 &0 &1 | ||
| + | \end{pmatrix} | ||
| + | \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
| + | \text{Rows 1, 3 and 5 of the parity-check matrix} \hspace{0.05cm},</math> | ||
| + | ::<math>\underline{z}_{\rm E} = (z_2, z_4)\hspace{0.05cm},\hspace{0.35cm} { \boldsymbol{\rm H} }_{\rm E}= | ||
| + | \begin{pmatrix} | ||
| + | 0 &0\\ | ||
| + | 1 &1\\ | ||
| + | 1 &0 | ||
| + | \end{pmatrix} | ||
| + | \hspace{1.05cm}\Rightarrow\hspace{0.3cm} | ||
| + | \text{Rows 2 and 4 of the parity-check matrix} \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Remembering that in $\rm GF(2)$ subtraction equals addition, the above equation can be represented as follows: | ||
| + | |||
| + | ::<math>{ \boldsymbol{\rm H} }_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} | ||
| + | + | ||
| + | { \boldsymbol{\rm H} }_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= \underline{0}^{\rm T} | ||
| + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| + | { \boldsymbol{\rm H} }_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= | ||
| + | { \boldsymbol{\rm H} }_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} | ||
| + | \begin{pmatrix} | ||
| + | 0 &0\\ | ||
| + | 1 &1\\ | ||
| + | 1 &0 | ||
| + | \end{pmatrix} \cdot | ||
| + | \begin{pmatrix} | ||
| + | z_2 \\ | ||
| + | z_4 | ||
| + | \end{pmatrix} = | ||
| + | \begin{pmatrix} | ||
| + | 1 &1 &0\\ | ||
| + | 1 &0 &0\\ | ||
| + | 0 &0 &1 | ||
| + | \end{pmatrix} \cdot | ||
| + | \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | 1 | ||
| + | \end{pmatrix} = \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | 1 | ||
| + | \end{pmatrix} | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | *This leads to a linear system of equations with two equations for the unknown $z_2$ and $z_4$ $($each $0$ or $1)$. | ||
| + | |||
| + | *From the last row follows $z_2 = 1$ and from the second row $z_2 + z_4 = 0$ ⇒ $z_4 = 1$. This gives the allowed code word $\underline{z} \rm = (0, 1, 0, 1, 1)$.}}<br> | ||
| + | |||
| + | == Exercises for the chapter == | ||
| + | <br> | ||
| + | [[Aufgaben:Exercise_1.11:_Syndrome_Decoding|Exercise 1.11: Syndrome Decoding]] | ||
| − | + | [[Aufgaben:Exercise_1.11Z:_Syndrome_Decoding_again|Exercise 1.11Z: Syndrome Decoding again]] | |
| − | + | [[Aufgaben:Exercise_1.12:_Hard_Decision_vs._Soft_Decision|Exercise 1.12: Hard Decision vs. Soft Decision]] | |
| − | + | [[Aufgaben:Exercise_1.12Z:_Comparison_of_HC_(7,_4,_3)_and_HC_(8,_4,_4)|Exercise 1.12Z: Comparison of HC (7, 4, 3) and HC (8, 4, 4)]] | |
| − | + | [[Aufgaben:Exercise_1.13:_Binary_Erasure_Channel_Decoding|Exercise 1.13: Binary Erasure Channel Decoding]] | |
| + | [[Aufgaben:Exercise_1.13Z:_Binary_Erasure_Channel_Decoding_again|Exercise 1.13Z: Binary Erasure Channel Decoding again]] | ||
{{Display}} | {{Display}} | ||
Latest revision as of 17:17, 30 November 2022
Contents
Block diagram and requirements
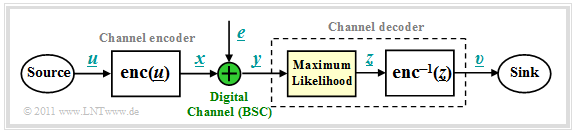
We start from the block diagram already shown in the chapter $\text{Channel Models and Decision Structures}$ where the digital channel model used is mostly the $\text{Binary Symmetric Channel}$ $\rm (BSC)$.
For code word estimation, we use the "Maximum Likelihood Decision" $\rm (ML)$, which for binary codes ⇒ $\underline{x} \in {\rm GF}(2^n)$ at the block level gives the same result as the $\text{MAP Receiver}$.
The task of the channel decoder can be described as follows:
- The vector $\underline{v}$ after decoding (at the sink) should match the information word $\underline{u}$ as well as possible.
- That is: The »block error probability« should be as small as possible:
- \[{ \rm Pr(block\:error)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm minimum}\hspace{0.05cm}.\]
- Because of assignments $\underline{x} = {\rm enc}(\underline{u})$ resp. $\underline{v} = {\rm enc}^{-1}(\underline{z})$ also holds:
- \[{ \rm Pr(block\:error)} = { \rm Pr}( \underline{z} \ne \underline{x}) \stackrel{!}{=} { \rm minimum}\hspace{0.05cm}.\]
- Sought is the most likely sent code word $\underline{y} = \underline{x} +\underline{e}$ for the given received word $\underline{x}_i$, which is passed on as result $\underline{z}$:
- \[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.\]
- For the BSC model, both $\underline{x}_i \in {\rm GF}(2^n)$ and $\underline{y} \in {\rm GF}(2^n)$, so the maximum likelihood decision rule can also be written using the $\text{Hamming distance}$ $d_{\rm H}( \underline{y}, \, \underline{x}_i)$:
- \[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]
Principle of syndrome decoding
Assumed here is a $(n, \, k)$ block code with the parity-check matrix $\boldsymbol{\rm H}$ and the systematic code words
- \[\underline{x}\hspace{0.05cm} = (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) = (u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k, p_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, p_{n-k})\hspace{0.05cm}. \]
With the error vector $\underline{e}$ then applies to the received word:
- \[\underline{y} = \underline{x} + \underline{e} \hspace{0.05cm}, \hspace{0.4cm} \underline{y} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{x} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{e} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}.\]
A bit error at position $i$ ⇒ $y_i ≠ x_i$ is expressed by the »error coefficient« $e_i = 1$.
$\text{Definition:}$ The »syndrome« $\underline{s} = (s_0, s_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, s_{m-1})$ is calculated (as row resp. column vector) from the received word $\underline{y}$ and the parity-check matrix $\boldsymbol{\rm H}$ as follows:
- \[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T}\hspace{0.3cm}{\rm bzw.}\hspace{0.3cm} \underline{s}^{\rm T} = { \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T}\hspace{0.05cm}.\]
- The vector length of $\underline{s}$ is equal to $m = n-k$ $($row number of $\boldsymbol{\rm H})$.
The syndrome $\underline{s}$ shows the following characteristics:
- Because of the equation $\underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{0}$ the syndrome $\underline{s}$ does not depend on the code word $\underline{x}$ but solely on the error vector $\underline{e}$:
- \[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} = \hspace{0.05cm} \underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} + \hspace{0.05cm} \underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} = \hspace{0.05cm} \underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} \hspace{0.05cm}.\]
- For sufficiently few bit errors, $\underline{s}$ provides a clear indication of the error locations, allowing full error correction.
$\text{Example 1:}$ Starting from the systematic $\text{(7, 4, 3)}$ Hamming code, the following result is obtained for the received vector $\underline{y} = (0, 1, 1, 1, 0, 0, 1)$:
- \[{ \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} = \underline{s}^{\rm T} \hspace{0.05cm}.\]
Comparing the syndrome with the $\text{parity-check equations}$ of the Hamming code, we see that
- most likely the fourth symbol $(x_4 = u_4)$ of the code word has been falsified,
- the code word estimator will thus yield the result $\underline{z} = (0, 1, 1, 0, 0, 0, 1)$,
- the decision is correct only if only one bit was falsified during transmission.
Below are the required corrections for the $\text{(7, 4, 3)}$ Hamming code resulting from the calculated syndrome $\underline{s}$ corresponding to the columns of the parity-check matrix:
- \[\underline{s} = (0, 0, 0) \hspace{0.10cm} \Rightarrow\hspace{0.10cm}{\rm no\hspace{0.15cm} correction}\hspace{0.05cm};\hspace{0.8cm}\underline{s} = (1, 0, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm}{\rm invert}\hspace{0.15cm}p_1\hspace{0.05cm};\]
- \[\underline{s} =(0, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}p_3\hspace{0.05cm};\hspace{1.63cm}\underline{s} = (1, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}u_1\hspace{0.05cm};\]
- \[\underline{s} =(0, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}p_2\hspace{0.05cm};\hspace{1.63cm}\underline{s} = (1, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}u_3\hspace{0.05cm};\]
- \[\underline{s} =(0, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}u_4\hspace{0.05cm};\hspace{1.63cm}\underline{s} = (1, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} {\rm invert}\hspace{0.15cm}u_2\hspace{0.05cm}. \]
Generalization of syndrome coding
We continue to assume the BSC channel model. This means:
- The received vector $\underline{y}$ and the error vector $\underline{e}$ are elements of ${\rm GF}(2^n)$.
- The possible code words $\underline{x}_i$ belong to the code $\mathcal{C}$, which spans a $(n-k)$-dimensional subspace of ${\rm GF}(2^n)$.
Under this assumption, we briefly summarize the results of the last sections:
- Syndrome decoding is a realization possibility of maximum likelihood decoding of block codes. One decides on the code word $\underline{x}_i$ with the least Hamming distance to the received word $\underline{y}$:
- \[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]
- But the syndrome decoding is also the search for the most probable error vector $\underline{e}$ that satisfies the condition $\underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{s}$. The "syndrome" is thereby determined by the equation
- $$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} .$$
- With the $\text{Hamming weight}$ $w_{\rm H}(\underline{e})$ the second interpretation can also be mathematically formulated as follows:
- \[\underline{z} = \underline{y} + {\rm arg} \min_{\underline{e}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} {\rm GF}(2^n)} \hspace{0.1cm} w_{\rm H}(\underline{e}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]
$\text{Conclusion:}$ Note that the error vector $\underline{e}$ as well as the received vector $\underline{y}$ is an element of ${\rm GF}(2^n)$ unlike the syndrome $\underline{s} \in {\rm GF}(2^m)$ with number $m = n-k$ of parity-check equations. This means, that
- the association between the syndrome $\underline{s}$ and the error vector $\underline{e}$ is not unique, but
- each $2^k$ error vectors lead to the same syndrome $\underline{s}$ which one groups together into a so-called "coset".
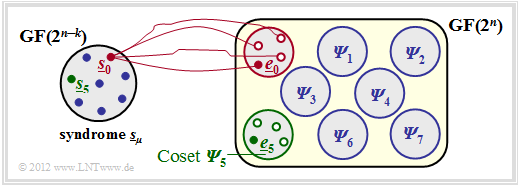
$\text{Example 2:}$ The facts shall be illustrated by the example with parameters $n = 5, \ k = 2$ ⇒ $m = n-k = 3$ .
You can see from this graph:
- The $2^n = 32$ possible error vectors $\underline{e}$ are divided into $2^m = 8$ cosets ${\it \Psi}_0$, ... , ${\it \Psi}_7$. Explicitly drawn here are only the cosets ${\it \Psi}_0$ and ${\it \Psi}_5$.
- All $2^k = 4$ error vectors of the coset ${\it \Psi}_\mu$ lead to the syndrome $\underline{s}_\mu$.
- Each minor class ${\it \Psi}_\mu$ has a "leader" $\underline{e}_\mu$, namely the one with the minimum Hamming weight.
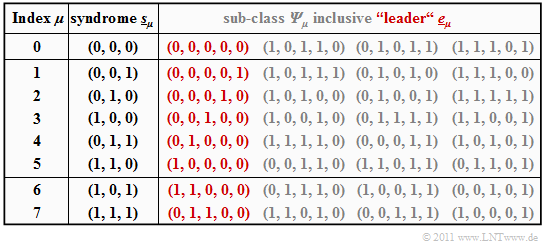
$\text{Example 3:}$ Starting from the systematic $\text{(5, 2, 3)}$ code $\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \big \}$ the syndrome decoding procedure is now described in detail.
- The generator matrix and the parity-check matrix are:
- \[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 &0 &1 &1 &0 \\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm},\]
- \[{ \boldsymbol{\rm H} } = \begin{pmatrix} 1 &0 &1 &0 &0 \\ 1 &1 &0 &1 &0 \\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.\]
- The table summarizes the final result. Note:
- The index $\mu$ is not identical to the binary value of $\underline{s}_\mu$.
- The order is rather given by the number of ones in the minor class leader $\underline{e}_\mu$.
- For example, the syndrome $\underline{s}_5 = (1, 1, 0)$ and the syndrome $\underline{s}_6 = (1, 0, 1)$.
- To derive this table, note:
- The row 1 refers to the syndrome $\underline{s}_0 = (0, 0, 0)$ and the associated cosets ${\it \Psi}_0$. The most likely error sequence here is $(0, 0, 0, 0, 0)$ ⇒ no bit error, which we call the "coset leader" $\underline{e}_0$.
- The other entries in the first row, namely $(1, 0, 1, 1, 0 )$, $(0, 1, 0, 1, 1)$ and $(1, 1, 1, 0, 1 )$, also each yield the syndrome $\underline{s}_0 = (0, 0, 0)$, but only result with at least three bit errors and are correspondingly unlikely.
- In rows 2 to 6, the respective coset leader $\underline{e}_\mu$ contains exactly a single "$1$" $(\mu = 1$, ... , $5)$. Here $\underline{e}_\mu$ is always the most likely error pattern of the class ${\it \Psi}_\mu$. The other group members result only with at least two bit errors.
- The syndrome $\underline{s}_6 = (1, 0, 1)$ is not possible with only one bit error. In creating the table, we then considered all "$5\text{ over }2 = 10$" error patterns $\underline{e}$ with weight $w_{\rm H}(\underline{e}) = 2$.
- The first found sequence with syndrome $\underline{s}_6 = (1, 0, 1)$ was chosen as coset leader $\underline{e}_6 = (1, 1, 0, 0)$ . With a different probing order, the sequence $(0, 0, 1, 0, 1)$ could also have resulted from ${\it \Psi}_6$.
- Similar procedure was followed in determining the leader $\underline{e}_7 = (0, 1, 1, 0, 0)$ of the cosets class ${\it \Psi}_7$ characterized by the uniform syndrome $\underline{s}_7 = (1, 1, 1)$. Also in the class ${\it \Psi}_7$ there is another sequence with Hamming weight $w_{\rm H}(\underline{e}) = 2$, namely $(1, 0, 0, 0, 1)$.
- The table only needs to be created once. First, the syndrome must be determined, e.g. for the received vector $\underline{y} = (0, 1, 0, 0, 1)$:
- \[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T} = \begin{pmatrix} 0 &1 &0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 1 &1 &0 \\ 0 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \\ \end{pmatrix} = \begin{pmatrix} 0 &1 &0 \end{pmatrix}= \underline{s}_2 \hspace{0.05cm}.\]
- Using the coset leader $\underline{e}_2 = (0, 0, 0, 1, 0)$ from the above table $($red entry for $\mu =2)$ finally arrives at the decoding result:
- \[\underline{z} = \underline{y} + \underline{e}_2 = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1) + (0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0) = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1) \hspace{0.05cm}.\]
$\text{Conclusion:}$ From these examples it is already clear that the »syndrome decoding means a considerable effort«, if one cannot use certain properties e.g. cyclic codes.
- For large block code lengths, this method fails completely. Thus, to decode a $\text{BCH code}$ $($the abbreviation stands for their inventors Bose, Chaudhuri, Hocquenghem$)$ with code parameters $n = 511$, $k = 259$ and $d_{\rm min} = 61$, one has to evaluate and store exactly $2^{511-259} \approx 10^{76}$ error patterns of length $511$.
- Happily, however, there are special decoding algorithms for these and also for other codes of large block length, which lead to success with less effort
.
Coding gain - bit error rate with AWGN
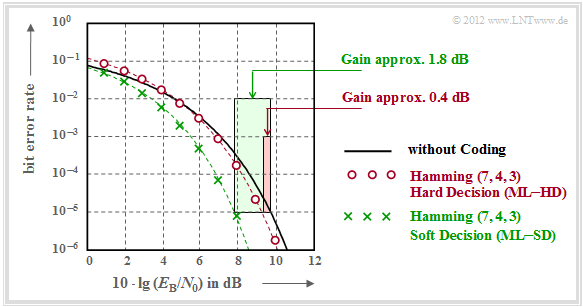
We now consider the $\text{bit error rate}$ for the following constellation:
- Hamming code $\text{HC (7, 4, 3)}$,
- AWGN–channel, characterized by the quotient $E_{\rm B}/N_0$ (in dB),
- Maximum Likelihood Decoder $\rm (ML)$ with
"Hard Decision" $\rm (HD)$ and "Soft Decision" $\rm (SD)$, resp.
It should be noted with regard to this graph:
- The black comparison curve applies e.g. to binary phase modulation $\rm (BPSK)$ without coding. For this one needs for the bit error rate $10^{-5}$ about $10 \cdot \lg \, E_{\rm B}/N_0 = 9.6 \, \rm dB$.
- The red circles apply to the $\text{HC (7, 4, 3)}$ and hard decisions of the maximum likelihood decoder $\text{(ML–HD)}$. Syndrome decoding is a possible realization form for this.
- This configuration brings an improvement over the comparison system only for $10 \cdot \lg \, E_{\rm B}/N_0 >6 \, \rm dB$. For $\rm BER =10^{-5}$ one only needs $10 \cdot \lg \, E_{\rm B}/N_0 \approx 9.2 \, \rm dB$.
- The green crosses for $\text{HC (7, 4, 3)}$ and $\text{soft decision}$ $\text{(ML–SD)}$ are below the red curve throughout the range. For $\rm BER =10^{-5}$ this gives $10 \cdot \lg \, E_{\rm B}/N_0 \approx 7.8 \, \rm dB$.
$\text{Definition:}$ We refer as »coding gain« of a considered system configuration,
- characterized by its code and
- the way it is decoded,
the smaller $10 \cdot \lg \, E_{\rm B}/N_0$ required for a given bit error rate $\rm (BER)$ compared to the comparison system $($without coding$)$:
- \[G_{\rm Code} (\hspace{0.05cm}\text{considered system} \hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm}) =10 \cdot {\rm lg}\hspace{0.1cm}{E}_{\rm B}/N_0 \hspace{0.15cm}(\hspace{0.05cm}\text{comparison system}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm})- 10 \cdot {\rm lg}\hspace{0.1cm}{E}_{\rm B}/N_0 \hspace{0.15cm}(\hspace{0.05cm}\text{considered system}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm}) \hspace{0.05cm}. \]
Applied to the above graph, one obtains:
\[G_{\rm Code} (\hspace{0.05cm}{\rm Hamming \hspace{0.1cm}(7,\hspace{0.02cm}4,\hspace{0.02cm}3), ML-HD}\hspace{0.05cm}|\hspace{0.05cm}{\rm BER} = 10^{-5}\hspace{0.05cm}) = 0.4\ {\rm dB}\hspace{0.05cm},\]
\[G_{\rm Code} (\hspace{0.05cm}{\rm Hamming \hspace{0.1cm}(7,\hspace{0.02cm}4,\hspace{0.02cm}3), ML-SD}\hspace{0.05cm}|\hspace{0.05cm}{\rm BER} = 10^{-5}\hspace{0.05cm}) = 1.8\ {\rm dB}\hspace{0.05cm}.\]
Decoding at the Binary Erasure Channel
Finally, it will be shown to what extent the decoder has to be modified
- if instead of the $\text{BSC model}$ ("Binary Symmetric Channel")
- the $\text{BEC model}$ ("Binary Erasure Channel") is used,
which does not produce errors but marks uncertain bits as "erasures".
$\text{Example 4:}$ We consider again as in $\text{Example 3}$ the systematic $\text{(5, 2, 3)}$ block code
- $$\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.3cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.3cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.3cm}(1, 1, 1, 0, 1) \big \}.$$
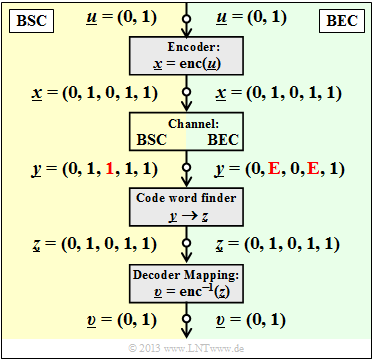
The graphic shows the system model and gives exemplary values for the individual vectors.
- The left part of the picture (yellow background) is valid for "BSC" with one bit error $(0 → 1)$ at the third bit.
- The right part of the picture (green background) is for "BEC" and shows two erasures $(\rm 1 → E)$ at the second and the fourth bit.
One recognizes:
- With BSC only $t = 1$ bit error (marked in red in the left part) can be corrected due to $d_{\rm min} = 3$. If one restricts oneself to error detection, this works up to $e= d_{\rm min} -1 = 2$ bit errors.
- For BEC, error detection makes no sense, because already the channel locates an uncertain bit as an "erasure" $\rm E$. The zeros and ones in the BEC received word $\underline{y}$ are safe. Therefore the error correction works here up to $e = 2$ erasures (marked in red in the right part) with certainty.
- Also $e = 3$ erasures are sometimes still correctable. So $\underline{y} \rm = (E, E, E, 1, 1)$ to $\underline{z} \rm = (0, 1, 0, 1, 1)$ to be corrected since no second code word ends with two ones. But $\underline{y} \rm = (0, E, 0, E, E)$ is not correctable because of the all zero word allowed in the code.
- If it is ensured that there are no more than two erasures in any received word, the BEC block error probability ${\rm Pr}(\underline{z} \ne \underline{x}) = {\rm Pr}(\underline{v} \ne \underline{u}) \equiv 0$. In contrast, the corresponding block error probability in the BSC model always has a value greater than $0$.
Since after the BEC each received word is either decoded correctly or not at all, we call here the block $\underline{y} → \underline{z}$ in the future "code word finder". An "estimation" takes place only in the BSC model.
But how does the decoding of a received word $\underline{y}$ with erasures work algorithmically?
$\text{Example 5:}$ Starting from the received word $\underline{y} \rm = (0, E, 0, E, 1)$ in $\text{Example 4}$ we formally set the output of the code word finder to $\underline{z} \rm = (0, z_2, 0, z_4, 1)$, where the symbols $z_2 \in \{0, \, 1\}$ and $z_4 \in \{0, \, 1\}$ are to be determined according to the following equation:
- \[\underline{z} \cdot { \boldsymbol{\rm H} }^{\rm T}= \underline{0} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H} } \cdot \underline{z}^{\rm T}= \underline{0}^{\rm T} \hspace{0.05cm}.\]
The task is now to implement this determination equation as efficiently as possible. The following calculation steps result:
- With the parity-check matrix $\boldsymbol{\rm H}$ of the $\text{(5, 2, 3)}$ block code and the vector $\underline{z} \rm = (0, z_2, 0, z_4, 1)$ is the above determination equation:
- \[{ \boldsymbol{\rm H} } \cdot \underline{z}^{\rm T} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ z_2 \\ 0 \\ z_4 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \hspace{0.05cm}.\]
- We sum up the "correct bits" (German: "korrekt" ⇒ subscript "K") to the vector $\underline{z}_{\rm K}$ and the "erased bits" to the vector $\underline{z}_{\rm E}$. Then we split the parity-check matrix $\boldsymbol{\rm H}$ into the corresponding submatrices $\boldsymbol{\rm H}_{\rm K}$ and $\boldsymbol{\rm H}_{\rm E}$:
- \[\underline{z}_{\rm K} =(0, 0, 1)\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm H} }_{\rm K}= \begin{pmatrix} 1 &1 &0\\ 1 &0 &0\\ 0 &0 &1 \end{pmatrix} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \text{Rows 1, 3 and 5 of the parity-check matrix} \hspace{0.05cm},\]
- \[\underline{z}_{\rm E} = (z_2, z_4)\hspace{0.05cm},\hspace{0.35cm} { \boldsymbol{\rm H} }_{\rm E}= \begin{pmatrix} 0 &0\\ 1 &1\\ 1 &0 \end{pmatrix} \hspace{1.05cm}\Rightarrow\hspace{0.3cm} \text{Rows 2 and 4 of the parity-check matrix} \hspace{0.05cm}.\]
- Remembering that in $\rm GF(2)$ subtraction equals addition, the above equation can be represented as follows:
- \[{ \boldsymbol{\rm H} }_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} + { \boldsymbol{\rm H} }_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= \underline{0}^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H} }_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H} }_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \begin{pmatrix} 0 &0\\ 1 &1\\ 1 &0 \end{pmatrix} \cdot \begin{pmatrix} z_2 \\ z_4 \end{pmatrix} = \begin{pmatrix} 1 &1 &0\\ 1 &0 &0\\ 0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \hspace{0.05cm}.\]
- This leads to a linear system of equations with two equations for the unknown $z_2$ and $z_4$ $($each $0$ or $1)$.
- From the last row follows $z_2 = 1$ and from the second row $z_2 + z_4 = 0$ ⇒ $z_4 = 1$. This gives the allowed code word $\underline{z} \rm = (0, 1, 0, 1, 1)$.
Exercises for the chapter
Exercise 1.11: Syndrome Decoding
Exercise 1.11Z: Syndrome Decoding again
Exercise 1.12: Hard Decision vs. Soft Decision
Exercise 1.12Z: Comparison of HC (7, 4, 3) and HC (8, 4, 4)
Exercise 1.13: Binary Erasure Channel Decoding
Exercise 1.13Z: Binary Erasure Channel Decoding again