Aufgaben:Exercise 2.5Z: Nyquist Equalization

• Return to book

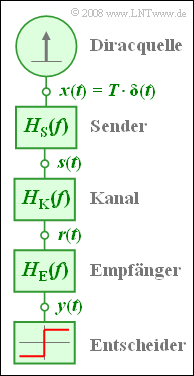
Ein digitales Basisbandübertragungssystem kann durch das dargestellte Blockschaltbild modelliert werden.

• Die Komponenten „Sender”, „Kanal” und „Empfänger” werden im Frequenzbereich durch $H_{\rm S}(f)$, $H_{\rm K}(f)$ und $H_{\rm E}(f)$ beschrieben .

• Der Gesamtfrequenzgang $H(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f)$ soll einen $\cos^2$–förmigen Verlauf haben:

$$H(f) = \left\{ \begin{array}{c} \cos^2\left(\frac{\pi}{2} \cdot f \cdot T \right) \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < 1/T,} \\ {\left|\hspace{0.005cm} f \hspace{0.05cm} \right| \ge 1/T.} \\ \end{array}$$

• Das Signal $y(t)$ vor dem (Schwellenwert–)Entscheider weist deshalb äquidistante Nulldurchgänge im Abstand $T$ auf.
• Vorausgesetzt wird dabei, dass die Quelle einen Diracimpuls $x(t)$ mit Gewicht $T$ abgibt (siehe Grafik).

Es wird darauf hingewiesen, dass es sich hierbei um ein so genanntes „Nyquistsystem” handelt. Wie im Buch Digitalsignalübertragung noch ausführlich diskutiert werden wird, stellen diese Nyquistsysteme eine wichtige Klasse digitaler Übertragungssysteme dar, da sich bei ihnen die sequenziell übertragenen Symbole nicht gegenseitig beeinflussen.

Für die Lösung dieser Aufgabe werden diese weiterreichenden Aspekte jedoch nicht benötigt. Es wird hier lediglich vorausgesetzt, dass

• der Sendeimpuls $y(t)$ rechteckförmig sei mit Impulsdauer $T$:

$$H_{\rm S}(f) = {\rm si}(\pi f T),$$

• der Kanal bis einschließlich Teilaufgabe (2) als ideal vorausgesetzt wird, während für die letzte Teilaufgabe gelten soll:

$$H_{\rm K}(f) = H_{\rm G}(f) = {\rm e}^{-\pi(f \cdot T)^2} .$$

Gesucht ist für beide Kanäle der Empfänger- und gleichzeitig Entzerrerfrequenzgang $H_{\rm E}(f)$, damit der Gesamtfrequenzgang die gewünschte Nyquistform aufweist.

Hinweise:

• Die Aufgabe gehört zum Kapitel Lineare Verzerrungen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Als bekannt vorausgesetzt wird die folgende trigonometrische Beziehung:

$$\frac{\cos^2(\alpha /2)}{\sin(\alpha )} = \frac{1}{2} \cdot {\rm cot}(\alpha /2) .$$

Fragebogen

1

Berechnen Sie den Ausgangssignalwert zum Zeitpunkt $t = 0$.

$y(t = 0) \ = $

2

Zunächst sei $H_{\rm K}(f) = 1$. Berechnen Sie für diesen Fall den Frequenzgang $H_{\rm E}(f)$. Welche Werte ergeben sich bei den nachfolgend genannten Frequenzen?

$\rm idealer \; Kanal:$   $|H_E(f \cdot T = 0)| \ =$

$|H_E(f \cdot T = 0.25)|\ =$

$|H_E(f \cdot T = 0.50)|\ =$

$|H_E(f \cdot T = 0.75)|\ =$

$|H_E(f \cdot T = 1.00)|\ =$

3

Berechnen Sie $H_{\rm E}(f)$ für den gaußförmigen Kanal entsprechend der Angabe.

$\rm Gausskanal:$   $|H_E(f \cdot T = 0)|\ =$

$|H_E(f \cdot T = 0.25)| \ =$

$|H_E(f \cdot T = 0.50)|\ =$

$|H_E(f \cdot T = 0.75)|\ =$

$|H_E(f \cdot T = 1.00)|\ =$

Musterlösung

Solution

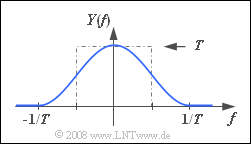
(1)  Mit dem konstanten Spektrum $X(f) = T$ erhält man für die Spektralfunktion des Empfängerausgangssignals $y(t)$:

$$Y(f)= T \cdot {H(f)}.$$

Der Signalwert bei $t = 0$ ist gleich der Fläche unter $`Y(f)$. Wie aus der nebenstehenden Skizze hervorgeht, ist diese gleich $1$. Daraus folgt: $y(t = 0)\; \underline{= 1}$.

(2)  Aus der Bedingung $H_{\rm S}(f) \cdot H_{\rm E}(f) = H(f)$ folgt im betrachteten Bereich:

$$H_{\rm E}(f)= \frac{H(f)}{H_{\rm S}(f)} = \frac{\cos^2(\pi f T/2)}{\sin(\pi f T)/(\pi f T)}.$$

Wegen $\cos(0) = 1$ und ${\rm si}(0) = 1$ gilt auch $H_{\rm E}(f = 0)\;\underline{=1}$.

Mit der gegebenen trigonometrischen Umformung gilt weiter:

$$H_{\rm E}(f) = \frac{\pi f T}{2} \cdot {\rm cot}\left( \frac{\pi f T}{2}\right),$$

$$H_{\rm E}(f \cdot T = 0.25) = {\pi }/{8} \cdot {\rm cot}\left( 22.5^{\circ}\right) = {\pi }/{8} \cdot 2.414 = \hspace{0.15cm}\underline{0.948},$$

$$H_{\rm E}(f \cdot T = 0.50) = {\pi }/{4} \cdot {\rm cot}\left( 45^{\circ}\right) = {\pi }/{4} \cdot 1 \hspace{0.15cm}\underline{= 0.785},$$

$$ H_{\rm E}(f \cdot T = 0.75) = {3 \pi }/{8} \cdot {\rm cot}\left( 67.5^{\circ}\right) = {3 \pi }/{8} \cdot 0.414 \hspace{0.15cm}\underline{= 0.488},$$

$$ H_{\rm E}(f \cdot T = 1.00)= { \pi }/{2} \cdot {\rm cot}\left( 90^{\circ}\right) ={ \pi }/{2} \cdot 0 \hspace{0.15cm}\underline{ = 0}.$$

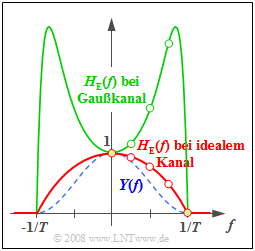
(3)  Unter Berücksichtigung des Gaußkanals gilt: $$H_{\rm E}(f)= \frac{H(f)}{H_{\rm S}(f) \cdot H_{\rm K}(f)} = H_{\rm E}^{(2)}(f)\cdot {\rm e}^{\pi (f T)^2}.$$

Hierbei bezeichnet $H_{\rm E}^{(2)}(f)$ den bei der Teilaufgabe (2) berechneten Entzerrerfrequenzgang unter der Voraussetzung eines idealen Kanals. Man erhält folgende numerische Ergebnisse: $$H_{\rm E}(f\cdot T = 0) = 1 \cdot {\rm e}^{0} \hspace{0.15cm}\underline{= 1},$$ $$H_{\rm E}(f \cdot T = 0.25) = 0.948 \cdot 1.217 \hspace{0.15cm}\underline{= 1.154},$$ $$H_{\rm E}(f \cdot T = 0.50) = 0.785 \cdot 2.193 \hspace{0.15cm}\underline{= 1.722},$$ $$H_{\rm E}(f \cdot T = 0.75) = 0.488 \cdot 5.854 \hspace{0.15cm}\underline{= 2.857},$$ $$H_{\rm E}(f \cdot T = 1.00) = 0 \cdot 23.141 \hspace{0.15cm}\underline{= 0}.$$

Die grüne Kurve in der zweiten Grafik fasst die Ergebnisse dieser Aufgabe zusammen.