Difference between revisions of "Digital Signal Transmission/Optimization of Baseband Transmission Systems"
| Line 278: | Line 278: | ||
Es wird von folgenden Voraussetzungen ausgegangen: | Es wird von folgenden Voraussetzungen ausgegangen: | ||
*Der Sendegrundimpuls $g_s(t)$ sei NRZ–rechteckförmig; bei Spitzenwertbegrenzung ist dies optimal.<br> | *Der Sendegrundimpuls $g_s(t)$ sei NRZ–rechteckförmig; bei Spitzenwertbegrenzung ist dies optimal.<br> | ||
| − | *Der Gesamtfrequenzgang $H_{\rm S}(f) \cdot H_{\rm E}(f) =H_{\rm Nyq}(f)$ erfülle die Nyquistbedingung und werde durch einen Cosinus–Rolloff–Tiefpass $H_{\rm CRO}(f)$ beschrieben. | + | *Der Gesamtfrequenzgang $H_{\rm S}(f) \cdot H_{\rm E}(f) =\sqrt{H_{\rm Nyq}(f)}$ erfülle die Nyquistbedingung und werde durch einen Cosinus–Rolloff–Tiefpass $H_{\rm Nyq}(f) = H_{\rm CRO}(f)$ beschrieben. |
*Da die Impulsamplitude $g_0$ unabhängig vom Rolloff–Faktor $r$ ist, lässt sich hier die SNR–Maximierung auf die Minimierung der Rauschleistung vor dem Entscheider zurückführen: | *Da die Impulsamplitude $g_0$ unabhängig vom Rolloff–Faktor $r$ ist, lässt sich hier die SNR–Maximierung auf die Minimierung der Rauschleistung vor dem Entscheider zurückführen: | ||
:$$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty}|H_{\rm E}(f)|^2 \,{\rm d} f\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum,} | :$$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty}|H_{\rm E}(f)|^2 \,{\rm d} f\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum,} | ||
| Line 301: | Line 301: | ||
*Das absolute Optimum bei Spitzenwertbegrenzzung ⇒ $\eta_{\rm A}= 1$ ergibt sich nur mit einem rechteckförmigen Sendegrundimpuls $g_s(t)$ und einer ebenfalls rechteckförmige Empfangsfilter–Impulsantwort $h_{\rm E}(t)$ gleicher Breite $T$. | *Das absolute Optimum bei Spitzenwertbegrenzzung ⇒ $\eta_{\rm A}= 1$ ergibt sich nur mit einem rechteckförmigen Sendegrundimpuls $g_s(t)$ und einer ebenfalls rechteckförmige Empfangsfilter–Impulsantwort $h_{\rm E}(t)$ gleicher Breite $T$. | ||
*Das beste Cosinus-Rolloff-Nyquistspektrum mit $r = 0.8$ (blaue Kurve) ist gegenüber dem Matched-Filter (violett-gestrichelte Kurve) um ca. $0.5 \ \rm dB$ schlechter, da die Fläche unter der blauen Kurve um ca. $12\%$ größer ist als die Fläche unter der violetten Kurve. | *Das beste Cosinus-Rolloff-Nyquistspektrum mit $r = 0.8$ (blaue Kurve) ist gegenüber dem Matched-Filter (violett-gestrichelte Kurve) um ca. $0.5 \ \rm dB$ schlechter, da die Fläche unter der blauen Kurve um ca. $12\%$ größer ist als die Fläche unter der violetten Kurve. | ||
| − | *Die }} | + | *Die so genannte [[Digitalsignalübertragung/Optimierung_der_Basisbandübertragungssysteme#Wurzel.E2.80.93Nyquist.E2.80.93Systeme|Wurzel–Wurzel–Konfiguration]] ⇒ $H_{\rm S}(f) \cdot H_{\rm E}(f) =\sqrt{H_{\rm CRO}(f)}$macht also nur Sinn, wenn man von Leistungsbegrenzung ausgeht.}} |
Revision as of 11:09, 21 August 2017
Contents
- 1 Voraussetzungen und Optimierungskriterium
- 2 Leistungs– und Spitzenwertbegrenzung
- 3 Systemoptimierung bei Leistungsbegrenzung
- 4 Wurzel–Nyquist–Systeme
- 5 Systemoptimierung bei Spitzenwertbegrenzung
- 6 Optimierung des Rolloff–Faktors bei Spitzenwertbegrenzung
- 7 Aufgaben zum Kapitel
- 8 Quellenverzeichnis
Voraussetzungen und Optimierungskriterium
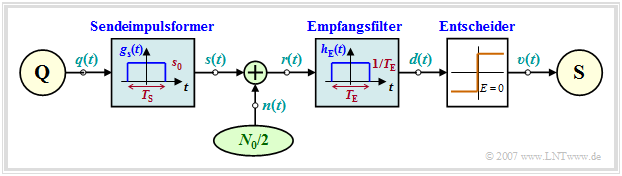
Für dieses Kapitel „Optimierung der Basisbandübertragungssysteme” gilt das folgende Blockschaltbild:
Wenn nicht explizit anders angegeben, wird im Folgenden von folgenden Voraussetzungen ausgegangen:
- Die Übertragung erfolgt binär, bipolar und redundanzfrei. Der Abstand zwischen den Symbolen ist $T$ und die (äquivalente) Bitrate $R = 1/T$. Mehrstufige und/oder redundante Systeme werden erst im Hauptkapitel 2: Codierte und mehrstufige Übertragung dieses Buches behandelt.
- Der Sendegrundimpuls $g_s(t)$ ist rechteckförmig und weist die Amplitude $s_0$ sowie die Impulsdauer $T_{\rm S} \le T$ auf. Stimmt die Sendeimpulsdauer $T_{\rm S}$ mit der Symboldauer $T$ überein, so spricht man von NRZ–Rechteckimpulsen. Im Fall $T_{\rm S} < T$ liegt ein RZ–Format vor.
- Als Übertragungskanal wird das AWGN–Modell mit der (einseitigen) Rauschleistungsdichte $N_0$ verwendet, so dass für das Empfangssignal $r(t) = s(t) + n(t)$ gilt. Die für systemtheoretische Untersuchungen besser geeignete zweiseitige Rauschleistungsdichte beträgt somit $N_0/2$.
- Die Impulsantwort $h_{\rm E}(t)$ des Empfangsfilters ist ebenfalls rechteckförmig, allerdings der mit Breite $T{\rm E}$ und der Höhe $1/T{\rm E}$. Daraus folgt für den Gleichsignalübertragungsfaktor $H_{\rm E}(f = 0) = 1$. Nur im Sonderfall $T_{\rm E} = T_{\rm S} $ kann man $H_{\rm E}(f)$ als Matched–Filter bezeichnen.
- Um Impulsinterferenzen auszuschließen, muss bei der Optimierung stets die Randbedingung $T_{\rm S} + T_{\rm E} \le 2T$ eingehalten werden. Impulsinterferenzen werden erst im Hauptkapitel 3: Impulsinterferenzen und Entzerrungsverfahren dieses Buches betrachtet.
- Zur Gewinnung der Sinkensymbolfolge wird ein einfacher Schwellenwertentscheider mit optimaler Entscheiderschwelle $E = 0$ und optimalen Detektionszeitpunkten (bei $\nu \cdot T$) verwendet.
Unter Systemoptimierung verstehen wir hier, die Parameter $T_{\rm S}$ und $T_{\rm E}$ von Sendegrundimpuls $g_s(t)$ und Empfangsfilter–Impulsantwort $h_{\rm E}(t)$ so zu bestimmen, dass die Bitfehlerwahrscheinlichkeit $p_{\rm B}$den kleinstmöglichen Wert annimmt.
Leistungs– und Spitzenwertbegrenzung
Die Optimierung der Systemgrößen wird entscheidend dadurch beeinflusst, ob als Nebenbedingung der Optimierung Leistungsbegrenzung oder Spitzenwertbegrenzung des Sendesignals gefordert wird.
$\text{Definition:}$ Unter Leistungsbegrenzung versteht man, dass die (mittlere) Sendeleistung $P_{\rm S}$ einen vorgegebenen Maximalwert $P_\text{S, max}$ nicht überschreiten darf:
- $$P_{\rm S}= {\rm E}[s(t)^2] = \overline{s(t)^2} \le P_{\rm S,\hspace{0.05cm} max}\hspace{0.05cm}.$$
Um die minimale Fehlerwahrscheinlichkeit zu erzielen, wird man natürlich die mittlere Sendeleistung $P_{\rm S}$ im erlaubten Bereich möglichst groß wählen. Deshalb wird im Folgenden stets $P_{\rm S} = P_\text{S, max}$ gesetzt.
Die Frage, ob als Nebenbedingung der Optimierung tatsächlich von Leistungsbegrenzung ausgegangen werden kann, hängt von den technischen Randbedingungen ab. Diese Annahme ist insbesondere bei Funkübertragungssystemen gerechtfertigt, unter Anderem deshalb, weil die als „Elektrosmog” bekannte Beeinträchtigung von Mensch und Tier in starkem Maße von der (mittleren) Strahlungsleistung abhängt.
Anzumerken ist, dass ein Funkübertragungssystem natürlich nicht im Basisband arbeitet. Die hier am Beispiel der Basisbandübertragung definierten Beschreibungsgrößen werden aber im Hauptkapitel 4: Verallgemeinerte Beschreibung digitaler Modulationsverfahren dieses Buches dahingehend modifiziert, dass sie auch für digitale Trägerfrequenzsysteme anwendbar sind.
$\text{Definition:}$ Von Spitzenwertbegrenzung spricht man immer dann, wenn der Aussteuerbereich der Sendeeinrichtung begrenzt ist. Bei bipolarer Signalisierung lautet die entsprechende Bedingung: \[\vert s(t) \vert \le s_0\hspace{0.4cm}{\rm{f\ddot{u}r} }\hspace{0.15cm}{\rm alle}\hspace{0.15cm}t.\] Oft verwendet man anstelle von Spitzenwertbegrenzung auch den Begriff Amplitudenbegrenzung, der aber den Sachverhalt nicht ganz richtig wiedergibt.
Natürlich wird auch bei Spitzenwertbegrenzung die Leistung begrenzt, aber nicht die mittlere, sondern die Spitzenleistung. Die Nebenbedingung „Spitzenwertbegrenzung” ist zum Beispiel dann sinnvoll und sogar notwendig, wenn
- der Aussteuerbereich des Senders wegen Nichtlinearitäten von Bauelementen und Endverstärkern beschränkt ist, oder
- die Nebensprechstörung zu keiner Zeit einen gewissen Wert nicht überschreiten darf. Hierauf ist insbesondere bei der Kommunikation über Zweidrahtleitungen zu achten.
$\text{Beispiel 1:}$ Sendegrundimpuls $g_s(t)$ und Empfangsfilter–Impulsantwort $h_{\rm E}(t)$ seien rechteckförmig. Die Amplitude $g_0$ des Ausgangsimpulses stimmt stets mit der Eingangsimpulsamplitude $s_0$ überein.
System A $(T_{\rm S} = T, \ T_{\rm E} = T)$:
- NRZ–Sendegrundimpuls,
- Matched–Filter, da $T_{\rm E} = T_{\rm S}$,
- Detektionsgrundimpuls: Dreieck,
- Energie pro Bit: $E_{\rm B} = s_0^2 \cdot T$,
- Rauschleistung: $\sigma_d^2 = N_0/(2T)$,
- Bestmögliche Konstellation
- Bitfehlerwahrscheinlichkeit:
- $$p_{\rm B}\hspace{-0.01cm} =\hspace{-0.01cm}{\rm Q} \left( g_0/\sigma_d\right)\hspace{-0.01cm}=\hspace{-0.01cm} {\rm Q} \left( \sqrt{ {2 \cdot s_0^2 \cdot T}/{N_0} }\right) = {\rm Q} \left( \sqrt{ {2 \cdot E_{\rm B} }/{N_0} }\right)\hspace{0.05cm}.$$
System B $(T_{\rm S} = T, \ T_{\rm E} = T/2)$:
- NRZ–Sendegrundimpuls,
- Kein Matched–Filter, da $T_{\rm E} \ne T_{\rm S}$,
- Detektionsgrundimpuls: Dreieck,
- Energie pro Bit: $E_{\rm B} = s_0^2 \cdot T$,
- Rauschleistung: $\sigma_d^2 = N_0/T$,
- Stets 3 dB schlechter als System A
- Bitfehlerwahrscheinlichkeit:
- $$p_{\rm B}\hspace{-0.01cm} =\hspace{-0.01cm}{\rm Q} \left( g_0/\sigma_d\right)\hspace{-0.01cm}=\hspace{-0.01cm} {\rm Q} \left( \sqrt{ {s_0^2 \cdot T}/{N_0} }\right) = {\rm Q} \left( \sqrt{ E_{\rm B} /{N_0} }\right)\hspace{0.05cm}.$$
System C $(T_{\rm S} = T/2, \ T_{\rm E} = T/2)$:
- RZ–Sendegrundimpuls,
- Matched–Filter, da $T_{\rm E} = T_{\rm S}$,
- Detektionsgrundimpuls: kleineres Dreieck,
- Energie pro Bit: $E_{\rm B} = 1/2 \cdot s_0^2 \cdot T$,
- Rauschleistung: $\sigma_d^2 = N_0/T$,
- Bei Leistungsbegrenzung wie System A,
- Bei Spitzenwertbegrenzung 3 dB schlechter,
- Bitfehlerwahrscheinlichkeit:
- $$p_{\rm B} ={\rm Q} \left( { {g_0}/{\sigma_d} }\right)= {\rm Q} \left( \sqrt{ { s_0^2 \cdot T}/{N_0} }\right)= {\rm Q} \left( \sqrt{2 \cdot {E_{\rm B} }/{N_0} }\right)\hspace{0.05cm}.$$
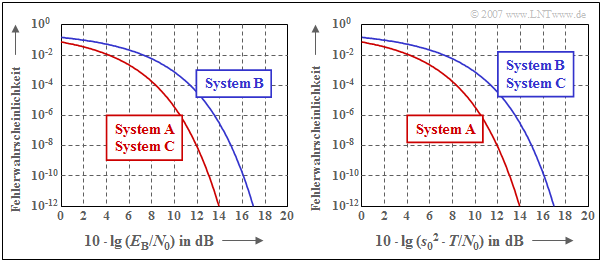
$\text{Beispiel 2:}$ Es gelten die gleichen Voraussetzungen wie im $\text{Beispiel 1}$. Die Grafik zeigt die Bitfehlerwahrscheinlichkeit $p_{\rm B}$
- in Abhängigkeit vom Verhältnis $E_{\rm B}/N_0$ (linkes Diagramm) und
- als Funktion von $s_0^2 \cdot T /N_0$ (rechtes Diagramm).
Es handelt sich um die Auswertung der im $\text{Beispiel 1}$ hergeleiteten Ergebnisse.
Diese beiden Diagramme in doppelt–logarithmischer Darstellung sind wie folgt zu interpretieren:
- Die linke Grafik vergleicht die Systeme bei gleicher mittlerer Leistung $(P_{\rm S})$ bzw. bei konstanter Energie pro Bit $(E_{\rm B})$. Da der Abszissenwert zusätzlich auf $N_0$ bezogen ist, gibt $p_{\rm B}(E_{\rm B}/N_0)$ den Sachverhalt auch für unterschiedliche Rauschleistungsdichten$N_0$ richtig wieder.
- Bei Leistungsbegrenzung sind die Konfigurationen A und C gleichwertig und stellen jeweils das Optimum dar. Wie auf den nächsten Seiten hergeleitet wird, liegt ein bei Leistungsbegrenzung optimales System immer dann vor, wenn $g_s(t)$ und $h_{\rm E}(t)$ formgleich sind (Matched–Filter). Die kleinere Leistung von System C wird durch die hier gewählte Abszisse ausgeglichen.
- Dagegen wird bei System B die Matched–Filter–Bedingung nicht eingehalten $(T_{\rm E} \ne T_{\rm S})$ und die Fehlerwahrscheinlichkeitskurve liegt nun um 3 dB rechts von der durch die Systeme A und C vorgegebenen Grenzkurve.
- Die rechte Grafik beschreibt das Optimierungsergebnis bei Spitzenwertbegrenzung, was an der Abszissenbeschriftung zu erkennen ist. Der Kurvenzug A (NRZ–Impuls, Matched–Filter) gibt auch hier die Grenzkurve an, die von keinem anderen System unterschritten werden kann.
- Die Kurve B in der rechten Grafik hat den genau gleichen Verlauf wie in der linken Darstellung, da wiederum NRZ–Sendeimpulse verwendet werden. Der Abstand von 3 dB zur Grenzkurve ist wieder auf die Nichteinhaltung der Matched–Filter–Bedingung zurückzuführen.
- Im Gegensatz zur linken Grafik liegt nun auch das Matched–Filter–System C um 3 dB rechts vom Optimum. Der Grund für diese Degradation ist, dass bei gleichem Spitzenwert (gleicher Spitzenleistung) das System C nur die halbe mittlere Leistung wie das System A bereitstellt.
Systemoptimierung bei Leistungsbegrenzung
Die Minimierung der Bitfehlerwahrscheinlichkeit $p_{\rm B} = {\rm Q} \left( \sqrt{\rho_d}\right)$ kann aufgrund des monotonen Funktionsverlaufs der komplementären Gaußschen Fehlerfunktion $ {\rm Q}(x)$ auf die Maximierung des Signal–zu–Rausch–Leistungsverhältnisses $\rho_d$ vor dem Schwellenwertentscheider (Detektions–SNR) zurückgeführt werden:
- $$p_{\rm B} = {\rm Q} \left( \sqrt{\rho_d}\right)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum}\hspace{1cm}\Rightarrow \hspace{1cm}\rho_d ={g_0^2}/{\sigma_d^2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Maximum}\hspace{0.05cm}.$$
Hierbei gibt $g_0 = g_d(t=0)$ die Amplitude des betrachteten Nyquistimpulses an und $\sigma_d^2$ bezeichnet die Detektionsstörleistung für das gegebene Empfangsfilter. Gleichzeitig muss sichergestellt werden, dass
- der Detektionsgrundimpuls $g_d(t) = g_s(t) \star h_{\rm E}(t)$ das erste Nyquistkriterium erfüllt, und
- die Energie des Sendegrundimpulses $g_s(t)$ einen vorgegebenen Wert $E_{\rm B}$ nicht überschreitet.
In den vorangegangenen Abschnitten wurde bereits mehrfach erwähnt, dass beim AWGN–Kanal mit der (einseitigen) Rauschleistungsdichte für das optimale System unter der Nebenbedingung der Leistungsbegrenzung gilt:
- $$p_{\rm B, \hspace{0.05cm}min} = {\rm Q} \left( \sqrt{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm} L}}}\right)\hspace{0.5cm}{\rm mit}\hspace{0.5cm} \rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm} L}}={2 \cdot E_{\rm B}}/{N_0}\hspace{0.05cm}.$$
Dieses Ergebnis benutzen wir für die folgende Definition:
$\text{Definition:}$ Der Systemwirkungsgrad bei Leistungsbegrenzung einer vorliegenden Konfiguration ist der Quotient aus dem tatsächlichen und dem größtmöglichen Signal–zu–Rausch–Leistungsverhältnis am Entscheider (Detektions–SNR):
- $$\eta_{\rm L} = \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}\vert \hspace{0.05cm} L} } }= \frac{g_0^2 /\sigma_d^2}{2 \cdot E_{\rm B}/N_0}\hspace{0.05cm}.$$
Nachfolgend wird bewiesen, dass
- die so definierte Größe tatsächlich die Bedingung $0 \le \eta_{\rm L} \le 1$ erfüllt und somit als „Wirkungsgrad” interpretiert werden kann,
- der Wert $\eta_{\rm L} = 1$ erreicht wird, wenn die Empfangsfilter–Impulsantwort $h_{\rm E}(t)$ formgleich mit dem Sendegrundimpuls $g_s(t)$ ist.
$\text{Beweis:}$ Der Beweis erfolgt im Frequenzbereich. Aus Darstellungsgründen normieren wir den Sendegrundimpuls:
- $$h_{\rm S}(t) = \frac{g_s(t)}{g_0 \cdot T} \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} H_{\rm S}(f) = \frac{G_s(f)}{g_0 \cdot T} \hspace{0.05cm}.$$
Damit hat $h_{\rm S}(t)$ die Einheit „1/s” und $H_{\rm S}(f)$ ist dimensionslos. Für die einzelnen Systemgrößen folgt daraus:
(1) Aufgrund des ersten Nyquistkriteriums muss gelten::
- $$ G_d(f) = G_s(f) \cdot H_{\rm E}(f) = G_{\rm Nyq}(f) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm S}(f) \cdot H_{\rm E}(f)= H_{\rm Nyq}(f)= \frac{G_{\rm Nyq}(f)}{g_0 \cdot T}\hspace{0.05cm}.$$
(2) Die Amplitude des Detektionsgrundimpulses ist gleich
- $$g_d(t=0) = g_0 \cdot T \cdot \int_{-\infty}^{+\infty}H_{\rm Nyq}(f) \,{\rm d} f = g_0\hspace{0.05cm}.$$
(3) Die Energie des Sendegrundimpulses ist wie folgt gegeben:
- $$E_{\rm B} = g_0^2 \cdot T^2 \cdot \int_{-\infty}^{+\infty} \vert H_{\rm S}(f)\vert ^2 \,{\rm d} f \hspace{0.05cm}.$$
(4) Die Detektionsstörleistung lautet:
- $$ \sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} \vert H_{\rm E}(f) \vert^2 \,{\rm d} f = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty}\frac {\vert H_{\rm Nyq}(f) \vert^2}{\vert H_{\rm S}(f) \vert^2} \,{\rm d} f\hspace{0.05cm}. $$
(5) Setzt man diese Teilergebnisse in die Gleichung für den Systemwirkungsgrad ein, so erhält man:
- $$\eta_{\rm L} = \left [ {T \cdot \int_{-\infty}^{+\infty} \vert H_{\rm S}(f) \vert^2 \,{\rm d} f \hspace{0.2cm} \cdot \hspace{0.2cm}T \cdot \int_{-\infty}^{+\infty}\frac { \vert H_{\rm Nyq}(f) \vert ^2}{ \vert H_{\rm S}(f) \vert^2} \,{\rm d} f } \right ]^{-1}\hspace{0.05cm}.$$
(6) Wir wenden nun auf den Ausdruck in der Klammer die Schwartzsche Ungleichung [BS01][1] an:
- $$\frac{1}{\eta_{\rm L} } = T \cdot \int_{-\infty}^{+\infty} \vert H_{\rm 1}(f) \vert^2 \,{\rm d} f \hspace{0.2cm} \cdot \hspace{0.2cm} T \cdot \int_{-\infty}^{+\infty} \vert H_{\rm 2}(f) \vert^2 \,{\rm d} f \hspace{0.3cm}\ge\hspace{0.3cm} \left [ T \cdot \int_{-\infty}^{+\infty} \vert H_{\rm 1}(f) \cdot H_{\rm 2}(f) \vert \,{\rm d} f \right ]^2$$
- $$\Rightarrow \hspace{0.3cm}\frac{1}{\eta_{\rm L} } = T \cdot \int_{-\infty}^{+\infty} \vert H_{\rm S}(f) \vert^2 \,{\rm d} f \hspace{0.1cm} \cdot \hspace{0.1cm} T \cdot \int_{-\infty}^{+\infty}\frac { \vert H_{\rm Nyq}(f) \vert ^2}{ \vert H_{\rm S}(f) \vert ^2} \,{\rm d} f \hspace{0.2cm}\ge\hspace{0.2cm} \left [ T \cdot \int_{-\infty}^{+\infty}\hspace{-0.5cm}H_{\rm Nyq}(f) \,{\rm d} f \right ]^2 = 1. $$
(7) Damit ist gezeigt, dass der Systemwirkungsgrad bei Leistungsbegrenzung tatsächlich die Bedingung $\eta_{\rm L} \le 1$ erfüllt.
(8) Die Auswertung zeigt, dass für $H_{\rm S, \hspace{0.05cm}opt}(f) = \gamma \cdot \sqrt{H_{\rm Nyq}(f)}$ in obiger Ungleichung das Gleichheitszeichen gilt:
- $$\gamma^2 \cdot T \cdot \int_{-\infty}^{+\infty}\hspace{-0.3cm} H_{\rm Nyq}(f) \,{\rm d} f \hspace{0.2cm} \cdot \hspace{0.2cm} \frac {1}{\gamma^2} \cdot T \cdot \int_{-\infty}^{+\infty} \hspace{-0.3cm}H_{\rm Nyq}(f) \,{\rm d} f = \left [ T \cdot \int_{-\infty}^{+\infty}\hspace{-0.3cm}H_{\rm Nyq}(f) \,{\rm d} f \right ]^2 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \eta_{\rm L} = 1 \hspace{0.05cm}.$$
(9) Dieses Ergebnis ist unabhängig vom Parameter $\gamma$, den wir deshalb vereinfachend zu $\gamma = 1$ setzen: $H_{\rm S, \hspace{0.05cm}opt}(f) = \sqrt{H_{\rm Nyq}(f)}$.
Wurzel–Nyquist–Systeme
Das wesentliche Ergebnis der Berechnungen auf den letzten Seiten war, dass beim optimalen Binärsystem unter der Nebenbedingung Leistungsbegrenzung
- der Detektionsgrundimpuls $g_d(t) = g_s(t) \star h_{\rm E}(t)$ die erste Nyquistbedingung erfüllen muss, und
- die Impulsantwort $h_{\rm E}(t)$ des Empfangsfilters formgleich mit dem Sendegrundimpuls $g_s(t)$ zu wählen ist; gleiches gilt für die zugehörigen Spektralfunktionen $H_{\rm E}(f)$ und $G_s(f)$
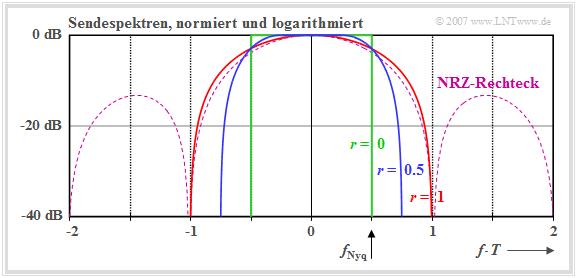
Sind sowohl $g_s(t)$ als auch $h_{\rm E}(t)$ rechteckförmig mit $T_{\rm S} = T_{\rm E} \le T$, so werden beide Bedingungen erfüllt. Nachteil dieser Konfiguration ist allerdings der große Bandbreitenbedarf aufgrund der nur langsam abfallenden, si–förmigen Spektralfunktionen $G_s(f)$ und $H_{\rm E}(f)$. In der unteren Grafik ist die Spektralfunktion des rechteckförmigen NRZ–Sendegrundimpulses als gestrichelte violette Kurve eingezeichnet.
Geht man von einem Nyquistspektrum mit Cosinus–Rolloff–Flanke ⇒ $H_{\rm E}(f) = H_{\rm CRO}(f)$ aus,
- $$<G_d(f) = G_s(f) \cdot H_{\rm E}(f) = g_0 \cdot T \cdot {H_{\rm CRO}(f)} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}G_s(f) = g_0 \cdot T \cdot \sqrt{H_{\rm CRO}(f)},\hspace{0.5cm}H_{\rm E}(f)= \sqrt{H_{\rm CRO}(f)}\hspace{0.05cm},$$
so ergeben sich für jeden Rolloff–Faktor $r$ günstigere Spektraleigenschaften und ein geringerer Bandbreitenbedarf.
Die folgende Grafik zeigt die normierten Sendespektren $G_s(f)/(g_0 \cdot T)$ in logarithmierter Darstellung für die drei Rolloff–Faktoren
- $r = 0$ (grüne Kurve),
- $r = 0.5$ (blaue Kurve), und
- $r = 1$ (rote Kurve).
Anmerkungen:
- Bei der Basisbandübertragung spielt der Bandbreitenbedarf nur eine untergeordnete Rolle.
- Die Grafik gilt aber auch für Trägerfrequenzsysteme bei Darstellung im äquivalenten Tiefpassbereich.
- Bei diesen Systemen spielt die Bandbreite eine wichtige Rolle. Jedes zusätzliches Hertz an Bandbreite kann sehr teuer sein.
Systemoptimierung bei Spitzenwertbegrenzung
Die Systemoptimierung hängt beim AWGN–Kanal mit der (einseitigen) Rauschleistungsdichte $N_0$ in starkem Maße davon ab, welche Nebenbedingung festgelegt wird:
- Bei Leistungsbegrenzung (gekennzeichnet durch den Index „L”) darf die Energie des Sendegrundimpulses $g_s(t)$ einen vorgegebenen Wert $E_{\rm B}$ nicht überschreiten. Hier gilt für die minimale Bitfehlerwahrscheinlichkeit und das maximale SNR:
- $$p_{\rm B, \hspace{0.05cm}min} = {\rm Q} \left( \sqrt{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm} L}}}\right)\hspace{0.5cm}{\rm mit}\hspace{0.5cm} \rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm} L}}={2 \cdot E_{\rm B}}/{N_0}\hspace{0.05cm}.$$
- Bei Spitzenwertbegrenzung (oder Amplitudenbegrenzung, gekennzeichnet durch den Index „A”) ist dagegen der Aussteuerbereich der Sendeeinrichtung begrenzt ⇒ $\vert s(t) \vert \le s_0\hspace{0.4cm}{\rm{f\ddot{u}r} }\hspace{0.15cm}{\rm alle}\hspace{0.15cm}t.$. Hier gilt für die entsprechenden Größen:
- $$p_{\rm B, \hspace{0.05cm}min} = {\rm Q} \left( \sqrt{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm}A}}}\right)\hspace{0.5cm}{\rm mit}\hspace{0.5cm} \rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm}A}}={2 \cdot s_0^2 \cdot T}/{N_0}\hspace{0.05cm}.$$
Für diesen zweiten Fall legen wir fest:
$\text{Definition:}$ Der Systemwirkungsgrad bei Amplitudenbegrenzung (Spitzenwertbegrenzung) lautet:
- $$\eta_{\rm A} = \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}\vert \hspace{0.05cm} A} } }= \frac{g_0^2 /\sigma_d^2}{ 2 \cdot s_0^2 \cdot T/N_0}\hspace{0.05cm}.$$
- Auch dieser Systemwirkungsgrad erfüllt die Bedingung $0 \le \eta_{\rm A} \le 1$.
- Es gibt nur ein einziges System mit dem Ergebnis $\eta_{\rm A} = 1$: NRZ–Rechteck–Sendegrundimpuls und daran angepasstes Empfangsfilter.
Ein Vergleich mit dem Systemwirkungsgrad bei Leistungsbegrenzung ⇒ $\eta_{\rm L}$ zeigt:
- $\eta_{\rm A}$ unterscheidet sich von $\eta_{\rm L}$ dadurch, dass nun im Nenner $s_0^2 \cdot T$ anstelle von $E_{\rm B}$ steht. Es gilt folgender Zusammenhang:
- $$\eta_{\rm A} = \frac{E_{\rm B}}{s_0^2 \cdot T} \cdot \eta_{\rm L}= \frac{\eta_{\rm L}}{C_{\rm S}^2}\hspace{0.05cm}.$$
- Hierbei bezeichnet der https://de.wikipedia.org/wiki/Scheitelfaktor Scheitelfaktor] (englisch: Crestfaktor) das Verhältnis von Maximalwert $s_0$ und Effektivwert $s_{\rm eff}$ des Sendesignals:
- $$C_{\rm S} = \frac{s_0}{\sqrt{E_{\rm B}/T}} = \frac{{\rm Max}[s(t)]}{\sqrt{{\rm E}[s^2(t)]}}= \frac{s_0}{s_{\rm eff}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{\rm eff} = \sqrt {E_{\rm B}/T}.$$
$\text{Beispiel 3:}$ Wir betrachten wie im Beispiel 1 drei unterschiedliche Konfigurationen mit jeweils rechteckförmigen Zeitfunktionen $g_s(t)$ und $h_{\rm E}(t)$ und geben hierfür die Systemwirkungsgrade an::
- System A: $\rho_d = {2 \cdot E_{\rm B} }/{N_0} = { 2 \cdot s_0^2 \cdot T}/{N_0}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\eta_{\rm L} = 1.0,\hspace{0.3cm}\eta_{\rm A} = 1.0\hspace{0.05cm}.$
- System B: $\rho_d = {E_{\rm B} }/{N_0} ={ s_0^2 \cdot T}/{N_0}\hspace{1.35cm}\Rightarrow \hspace{0.3cm}\eta_{\rm L} = 0.5,\hspace{0.3cm}\eta_{\rm A} = 0.5\hspace{0.05cm}.$
- System C: $\rho_d = {2 \cdot E_{\rm B} }/{N_0} = { s_0^2 \cdot T}/{N_0}\hspace{0.8cm}\Rightarrow \hspace{0.3cm}\eta_{\rm L} = 1.0,\hspace{0.3cm}\eta_{\rm A} = 0.5\hspace{0.05cm}.$
Man erkennt:
- Beim System B sind beide Systemwirkungsgrade aufgrund der fehlenden Anpassung $(T_{\rm E} \ne T_{\rm S})$ nur jeweils $0.5$.
- Beim System C hat zwar der Systemwirkungsgrad $\eta_{\rm L}$ wegen $T_{\rm E} = T_{\rm S}$ den Maximalwert $\eta_{\rm L} = 1$.
- Dagegen ist $\eta_{\rm A} = 0.5$, da der RZ–Impuls nicht die maximale Energie besitzt, die aufgrund der Spitzenwertbegrenzung erlaubt wäre.
- Der Crestfaktor hat hier den Wert $C_{\rm S} = \sqrt{2}$.
$\text{Beispiel 4:}$ Nun betrachten wir eine Wurzel–Nyquist–Konfiguration mit Cosinus–Rolloff–Gesamtfrequenzgang:
- $$G_s(f) = g_0 \cdot T \cdot \sqrt{H_{\rm CRO}(f)},\hspace{0.5cm}H_{\rm E}(f)= \sqrt{H_{\rm CRO}(f)} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} G_d(f) = g_0 \cdot T \cdot {H_{\rm CRO}(f)} = G_{\rm Nyq}(f)\hspace{0.05cm}.$$
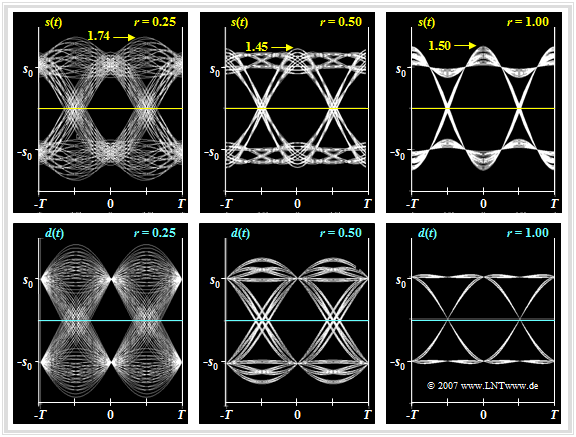
Die Grafik zeigt die Augendiagramme am Sender (oben) und am Empfänger (unten), jeweils für die Rolloff–Faktoren $r = 0.25$, $r = 0.5$ und $r = 0.1$. Es sei daran erinnert, dass eine solche Konfiguration unter der Nebenbedingung der Leistungsbegrenzung unabhängig vom Rolloff–Faktor $r$ optimal ist: $\eta_{\rm L} = 1$.
Man erkennt aus dieser Darstellung:
- Der Sendeimpuls $g_s(t)$ erfüllt nicht die Nyquistbedingung: Das Auge am Sender (obere Bildreihe) ist nicht vollständig geöffnet; der Maximalwert des Sendesignals ist größer als sein Effektivwert.
- Der Crestfaktor $C_{\rm S} = s_0/s_{\rm eff}$ wird mit kleinerem $r$ größer und damit der Wirkungsgrad $\eta_{\rm A} $ kleiner. Für $r = 0.5$ ergibt sich $C_{\rm S} \approx 1.45$ und damit $\eta_{\rm A} \approx 0.47$. Das Detektions–SNR ist dann um den Betrag $10 \cdot \lg \ \eta_{\rm A} \approx 3.2 \ \rm dB$ geringer als bei der Rechteck–Rechteck–Konfiguration.
- Im Grenzfall $r = 0$ gilt sogar $C_{\rm S} \to \infty$ und $\eta_{\rm A} \to 0$. Der Sendegrundimpuls $g_s(t)$ fällt hier noch langsamer als mit $1/t$ ab, und es gilt:
- $$\max_t\{ s(t) \} = \max_t \hspace{0.15cm}\big [ \sum_{(\nu)} a_\nu \cdot g_s ( t - \nu \cdot T)\ \big ]\rightarrow \infty\hspace{0.05cm}.$$
- Begrenzt man das Sendesignal $s(t)$ durch einen gegen $0$ gehenden Gewichtungsfaktor auf einen endlichen Maximalwert $s_0$, so führt dies zu einem geschlossenem Auge vor dem Entscheider.
Optimierung des Rolloff–Faktors bei Spitzenwertbegrenzung
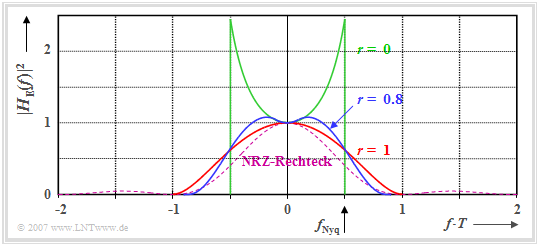
Es wird von folgenden Voraussetzungen ausgegangen:
- Der Sendegrundimpuls $g_s(t)$ sei NRZ–rechteckförmig; bei Spitzenwertbegrenzung ist dies optimal.
- Der Gesamtfrequenzgang $H_{\rm S}(f) \cdot H_{\rm E}(f) =\sqrt{H_{\rm Nyq}(f)}$ erfülle die Nyquistbedingung und werde durch einen Cosinus–Rolloff–Tiefpass $H_{\rm Nyq}(f) = H_{\rm CRO}(f)$ beschrieben.
- Da die Impulsamplitude $g_0$ unabhängig vom Rolloff–Faktor $r$ ist, lässt sich hier die SNR–Maximierung auf die Minimierung der Rauschleistung vor dem Entscheider zurückführen:
- $$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty}|H_{\rm E}(f)|^2 \,{\rm d} f\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum,} \hspace{0.5cm}{\rm wobei}\hspace{0.5cm} H_{\rm E}(f) =\frac {H_{\rm CRO}(f)}{{\rm si}(\pi f T)}\hspace{0.05cm}.$$
Die Grafik zeigt die Leistungsübertragungsfunktion $|H_{\rm E}(f)|^2$ für drei verschiedene Rolloff–Faktoren. Die Flächen unter diesen Kurven sind jeweils ein Maß für die Rauschleistung vor dem Entscheider.
Man erkennt aus dieser Darstellung:
- Der Rolloff–Faktor $r = 0$ (Rechteck) führt trotz des sehr schmalbandigen Empfangsfilters nur zum Wirkungsgrad $\eta_{\rm A} \approx 0.65$, da $H_{\rm E}(f)$ wegen der si-Funktion im Nenner mit wachsendem $f$ ansteigt.
- $r = 1$ bewirkt zwar ein doppelt so breites Spektrum, führt aber zu keiner Anhebung. Da die Fläche unter der roten Kurve kleiner ist als die grüne, ergibt sich ein besserer Wert: $\eta_{\rm A} \approx 0.88$.
- Der größte Systemwirkungsgrad ergibt sich für$r \approx 0.8$ (flaches Maximum) mit $\eta_{\rm A} \approx 0.89$. Hierfür erreicht man den bestmöglichen Kompromiss zwischen Bandbreite und Überhöhung.
- Durch Vergleich mit dem optimalen Frequenzgang $H_{\rm E}(f) = {\rm si}(\pi f T$ bei Spitzenwertbegrenzung, der zum Ergebnis $\sigma^2 = N_0/(2T)$ ⇒ $\eta_{\rm A}= 1$ führt, erhält man für den Systemwirkungsgrad:
- $$\eta_{\rm A} = \left [T \cdot \int_{-\infty}^{+\infty}\hspace{-0.15cm} |H_{\rm E}(f)|^2 \,{\rm d} f \right ]^{-1} \hspace{0.05cm}.$$
$\text{Fazit:}$
- Das absolute Optimum bei Spitzenwertbegrenzzung ⇒ $\eta_{\rm A}= 1$ ergibt sich nur mit einem rechteckförmigen Sendegrundimpuls $g_s(t)$ und einer ebenfalls rechteckförmige Empfangsfilter–Impulsantwort $h_{\rm E}(t)$ gleicher Breite $T$.
- Das beste Cosinus-Rolloff-Nyquistspektrum mit $r = 0.8$ (blaue Kurve) ist gegenüber dem Matched-Filter (violett-gestrichelte Kurve) um ca. $0.5 \ \rm dB$ schlechter, da die Fläche unter der blauen Kurve um ca. $12\%$ größer ist als die Fläche unter der violetten Kurve.
- Die so genannte Wurzel–Wurzel–Konfiguration ⇒ $H_{\rm S}(f) \cdot H_{\rm E}(f) =\sqrt{H_{\rm CRO}(f)}$macht also nur Sinn, wenn man von Leistungsbegrenzung ausgeht.
Aufgaben zum Kapitel
Quellenverzeichnis
- ↑ Bronstein, I.N.; Semendjajew, K.A.: Taschenbuch der Mathematik. 5. Auflage. Frankfurt: Harry Deutsch, 2001.