Difference between revisions of "Aufgaben:Exercise 1.7: Coding for Broadband ISDN"
m (Guenter verschob die Seite 1.7 Codierung bei B–ISDN nach Aufgabe 1.7: Codierung bei B–ISDN) |
|||
| Line 4: | Line 4: | ||
[[File:P_ID1630__Bei_A_1_7.png|right|frame|HDB3- und 1T2B-Codierung]] | [[File:P_ID1630__Bei_A_1_7.png|right|frame|HDB3- und 1T2B-Codierung]] | ||
| − | + | Bei herkömmlichem ISDN über Kupferleitungen wird der HDB3–Code verwendet – siehe [[Aufgaben:Aufgabe_1.5:_HDB3–Codierung|Aufgabe 1.5]]: Dieser wurde vom so genannten AMI–Code abgeleitet, | |
| + | *ist wie dieser ein Pseudoternärcode, | ||
| + | *vermeidet aber mehr als drei aufeinander folgende „$0$”–Symbole, | ||
| + | *indem die strenge AMI–Codierregel bei längeren Nullfolgen bewusst verletzt wird. | ||
| + | |||
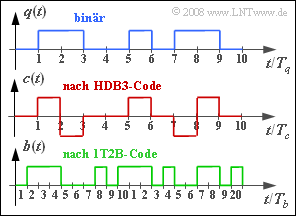
Die Grafik zeigt das HDB3–codierte Signal $c(t)$, das sich aus dem binären redundanzfreien Quellensignal $q(t)$ ergibt. Da im Quellensignal nicht mehr als drei aufeinanderfolgende Nullen auftreten, ist $c(t)$ identisch mit dem AMI–codierten Signal. | Die Grafik zeigt das HDB3–codierte Signal $c(t)$, das sich aus dem binären redundanzfreien Quellensignal $q(t)$ ergibt. Da im Quellensignal nicht mehr als drei aufeinanderfolgende Nullen auftreten, ist $c(t)$ identisch mit dem AMI–codierten Signal. | ||
| − | Das Ende der 1990–Jahre geplante Breitband–ISDN sollte Datenraten bis | + | Das Ende der 1990–Jahre geplante Breitband–ISDN sollte Datenraten bis 155 Mbit/s bereitstellen im Vergleich zu 144 kbit/s des herkömmlichen ISDN mit zwei B–Kanälen und einem D–Kanal. Um diese hohe Datenrate zu erreichen, musste |
| + | *zum einen eine neuere Technik (ATM) verwendet werden, | ||
| + | *zum zweiten aber auch das Übertragungsmedium gewechselt werden, von der Kupferleitung zur Glasfaser. | ||
| + | |||
| + | |||
| + | Da das HDB3–codierte Signal $c(t) ∈ \{–1, 0, +1\}$ aber mittels Licht nicht übertragen werden kann, war eine zweite Codierung erforderlich. Der hierfür vorgesehene 1T2B–Code ersetzt jedes Ternärsymbol durch zwei Binärsymbole. Das untere Diagramm zeigt beispielhaft das Binärsignal $b(t) ∈ \{0, 1\}$, das sich nach dieser '''1T2B–Codierung''' aus dem Signal $c(t)$ ergibt. | ||
| − | + | Gehen Sie bei dieser Aufgabe davon aus, dass die Bitrate des redundanzfreien Quellensignals $q(t)$ gleich $R_{q} = 2.048 \ \rm Mbit/s$ beträgt. Die jeweiligen Symboldauern der Signale $q(t), c(t)$ und $b(t)$ werden mit $T_{q}$, $T_{c}$ und $T_{b}$ bezeichnet. | |
| − | + | Die äquivalente Bitrate des pseudoternären Signals $c(t)$ ist $R_{c} = {\rm log_2}(3)/T_{c}$, woraus mit der (echten) Bitrate $R_{q} = 1/T_{q}$ des Quellensignals die relative Redundanz des AMI– bzw. HDB3–Codes berechnet werden kann: | |
| + | :$$r_{\rm HDB3} = \frac{R_c - R_q}{R_c}= 1 - \frac{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_c)} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
Für den 1T2B–Code kann eine ähnliche Gleichung aufgestellt werden, ebenso wie für die beiden Codes in Kombination. | Für den 1T2B–Code kann eine ähnliche Gleichung aufgestellt werden, ebenso wie für die beiden Codes in Kombination. | ||
| − | |||
| − | Die Aufgabe gehört zum [[Beispiele_von_Nachrichtensystemen/Weiterentwicklungen_von_ISDN|Weiterentwicklungen von ISDN]] | + | |
| + | ''Hinweise:'' | ||
| + | |||
| + | *Die Aufgabe gehört zum Kapitel [[Beispiele_von_Nachrichtensystemen/Weiterentwicklungen_von_ISDN|Weiterentwicklungen von ISDN]]. | ||
| + | * Die Redundanz wird im [[Digitalsignalübertragung/Grundlagen_der_codierten_Übertragung|Grundlagen der codierten Übertragung]] des Buches „Digitalsignalübertragung” definiert und an Beispielen verdeutlicht. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 16:30, 19 December 2017
Bei herkömmlichem ISDN über Kupferleitungen wird der HDB3–Code verwendet – siehe Aufgabe 1.5: Dieser wurde vom so genannten AMI–Code abgeleitet,
- ist wie dieser ein Pseudoternärcode,
- vermeidet aber mehr als drei aufeinander folgende „$0$”–Symbole,
- indem die strenge AMI–Codierregel bei längeren Nullfolgen bewusst verletzt wird.
Die Grafik zeigt das HDB3–codierte Signal $c(t)$, das sich aus dem binären redundanzfreien Quellensignal $q(t)$ ergibt. Da im Quellensignal nicht mehr als drei aufeinanderfolgende Nullen auftreten, ist $c(t)$ identisch mit dem AMI–codierten Signal.
Das Ende der 1990–Jahre geplante Breitband–ISDN sollte Datenraten bis 155 Mbit/s bereitstellen im Vergleich zu 144 kbit/s des herkömmlichen ISDN mit zwei B–Kanälen und einem D–Kanal. Um diese hohe Datenrate zu erreichen, musste
- zum einen eine neuere Technik (ATM) verwendet werden,
- zum zweiten aber auch das Übertragungsmedium gewechselt werden, von der Kupferleitung zur Glasfaser.
Da das HDB3–codierte Signal $c(t) ∈ \{–1, 0, +1\}$ aber mittels Licht nicht übertragen werden kann, war eine zweite Codierung erforderlich. Der hierfür vorgesehene 1T2B–Code ersetzt jedes Ternärsymbol durch zwei Binärsymbole. Das untere Diagramm zeigt beispielhaft das Binärsignal $b(t) ∈ \{0, 1\}$, das sich nach dieser 1T2B–Codierung aus dem Signal $c(t)$ ergibt.
Gehen Sie bei dieser Aufgabe davon aus, dass die Bitrate des redundanzfreien Quellensignals $q(t)$ gleich $R_{q} = 2.048 \ \rm Mbit/s$ beträgt. Die jeweiligen Symboldauern der Signale $q(t), c(t)$ und $b(t)$ werden mit $T_{q}$, $T_{c}$ und $T_{b}$ bezeichnet.
Die äquivalente Bitrate des pseudoternären Signals $c(t)$ ist $R_{c} = {\rm log_2}(3)/T_{c}$, woraus mit der (echten) Bitrate $R_{q} = 1/T_{q}$ des Quellensignals die relative Redundanz des AMI– bzw. HDB3–Codes berechnet werden kann:
- $$r_{\rm HDB3} = \frac{R_c - R_q}{R_c}= 1 - \frac{T_c \cdot {\rm log_2}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm log_2}\hspace{0.1cm}(M_c)} \hspace{0.05cm}.$$
Für den 1T2B–Code kann eine ähnliche Gleichung aufgestellt werden, ebenso wie für die beiden Codes in Kombination.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weiterentwicklungen von ISDN.
- Die Redundanz wird im Grundlagen der codierten Übertragung des Buches „Digitalsignalübertragung” definiert und an Beispielen verdeutlicht.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(1) Richtig ist Lösungsvorschlag 2, wie ein Vergleich der Signalverläufe $c(t)$ und $b(t)$ zeigt.
(2) Die Symboldauer (Bitdauer) von $q(t)$ beträgt $T_{q} \underline{ = 1/R_{q} = 0.488 \ \rm \mu s}$. Die Symboldauer $T_{c}$ des AMI–Codes (und des HDB3–Codes) ist genau so groß. Dagegen ist die Symboldauer (Bitdauer) nach der 1T2B–Codierung nur halb so groß: $T_{b} = T_{c}/2 \underline{= 0.244 \ \rm \mu s}$.
(3) Mit der angegebenen Gleichung ergibt sich mit $M_{q} = 2, M_{c} = 3$ und $T_{c} = T_{q}$:
- $$r_{\rm HDB3} = 1 - \frac{T_c \cdot {\rm ld}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm ld}\hspace{0.1cm}(M_c)} = 1 - \frac{1}{{\rm ld}\hspace{0.1cm}(3)} \hspace{0.15cm}\underline{= 36.9\,\%} \hspace{0.05cm}.$$
(4) asst man die Gleichung an den Coder 2 an, so erhält man mit $M_{c} = 3, M_{b} = 2, T_{b} = T_{c}/2$:
- $$r_{\rm 1T2B} = 1 - \frac{T_b \cdot {\rm ld}\hspace{0.1cm}(M_c)}{T_c \cdot {\rm ld}\hspace{0.1cm}(M_b)} = 1 - \frac{{\rm ld}\hspace{0.1cm}(3)}{2} \hspace{0.15cm}\underline{= 20.7\,\%} \hspace{0.05cm}.$$
(5) Die Redundanz erhält man, wenn man die angegebene Gleichung auf das Eingangssignal $q(t)$ und das Ausgangssignal $c(t)$ bezieht. Mit $M_{q} = M_{b} = 2$ und $T_{b} = T_{q}/2$ folgt daraus:
- $$r_{\rm HDB3+1T2B} = 1 - \frac{T_b \cdot {\rm ld}\hspace{0.1cm}(M_q)}{T_q \cdot {\rm ld}\hspace{0.1cm}(M_b)} = 1 - \frac{T_b}{T_q} \hspace{0.15cm}\underline{= 50\,\%} \hspace{0.05cm}.$$
Zum gleichen Ergebnis kommt man über die Rechnung
- $$1-r_{\rm HDB3+1T2B} \ = \ (1-r_{\rm HDB3}) \cdot (1-r_{\rm 1T2B}) =$$
- $$\hspace{2.7cm} \ = \ (1- 1 +\frac{1}{{\rm ld}\hspace{0.1cm}(3)}) \cdot (1-1+ \frac{{\rm ld}\hspace{0.1cm}(3)}{2}) = 50\,\% \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm}r_{\rm HDB3+1T2B}= 50\,\% \hspace{0.05cm}.$$