Difference between revisions of "Modulation Methods/Objectives of Modulation and Demodulation"
m (Text replacement - "[File:" to "[File:") |
m (Text replacement - "[[Signaldarstellung/" to "[[Signal_Representation/") |
||
| Line 33: | Line 33: | ||
Weiter ist anzumerken: | Weiter ist anzumerken: | ||
| − | *Das zur Übertragung anstehende Quellensignal $q(t)$ sei ein [[ | + | *Das zur Übertragung anstehende Quellensignal $q(t)$ sei ein [[Signal_Representation/Klassifizierung_von_Signalen#Analogsignale_und_Digitalsignale|Analogsignal]], zum Beispiel Sprache, Musik oder der Ausgang einer (analogen) Kamera. Das zugehörige Spektrum $Q(f)$ sei auf den Frequenzbereich $|f| ≤ B_{\rm NF}$ begrenzt, wobei der Index für „Niederfrequenz” steht. |
*Der mittlere Block in obigem Bild beinhaltet auch Störungen (Interferenzen, Übersprechen anderer Nutzer, Impulsstörungen durch Starkstromleitungen, etc.) und Rauschquellen wie Widerstands– und Halbleiterrauschen. Diese werden durch das [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)#Theorem_von_Wiener-Chintchine|Störleistungsdichtespektrum]] ${\it Φ}_n(f)$ erfasst. | *Der mittlere Block in obigem Bild beinhaltet auch Störungen (Interferenzen, Übersprechen anderer Nutzer, Impulsstörungen durch Starkstromleitungen, etc.) und Rauschquellen wie Widerstands– und Halbleiterrauschen. Diese werden durch das [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)#Theorem_von_Wiener-Chintchine|Störleistungsdichtespektrum]] ${\it Φ}_n(f)$ erfasst. | ||
| − | *Aufgabe eines solchen Nachrichtenübertragungssystems ist es, die im Quellensignal $q(t)$ enthaltene Nachricht bzw. Information – man beachte die [[ | + | *Aufgabe eines solchen Nachrichtenübertragungssystems ist es, die im Quellensignal $q(t)$ enthaltene Nachricht bzw. Information – man beachte die [[Signal_Representation/Prinzip_der_Nachrichtenübertragung#Nachricht_-_Information_-_Signal|unterschiedliche Bedeutung dieser Größen]] – zur räumlich entfernten Sinke zu übertragen mit der Maßgabe, dass sich das Sinkensignal $v(t)$ „möglichst wenig” von $q(t)$ unterscheidet. |
*Ein häufig auftretendes Problem ist, dass der Kanal für die direkte Übertragung des Quellensignals $q(t)$ ungeeignet ist, da dieses „ungünstige Frequenzen” beinhaltet. So kann ein Musiksignal mit Frequenzen bis ca. $\text{15 kHz}$ nicht direkt per Funk übertragen werden, da eine Funkausbreitung erst ab etwa $\text{100 kHz}$ möglich ist. | *Ein häufig auftretendes Problem ist, dass der Kanal für die direkte Übertragung des Quellensignals $q(t)$ ungeeignet ist, da dieses „ungünstige Frequenzen” beinhaltet. So kann ein Musiksignal mit Frequenzen bis ca. $\text{15 kHz}$ nicht direkt per Funk übertragen werden, da eine Funkausbreitung erst ab etwa $\text{100 kHz}$ möglich ist. | ||
| Line 208: | Line 208: | ||
[[File:Mod_T_1_1_S7_version2.png|right|frame|Zur Verdeutlichung von Zeitmultiplex]] | [[File:Mod_T_1_1_S7_version2.png|right|frame|Zur Verdeutlichung von Zeitmultiplex]] | ||
| − | *Die Signale $q_1(t), q_2(t)$ und $q_3(t)$ sind binär und werden durch Amplitudenkoeffizienten $(0$ oder $1)$ vollständig beschrieben. Es liegt eine [[ | + | *Die Signale $q_1(t), q_2(t)$ und $q_3(t)$ sind binär und werden durch Amplitudenkoeffizienten $(0$ oder $1)$ vollständig beschrieben. Es liegt eine [[Signal_Representation/Zeitdiskrete_Signaldarstellung|zeitdiskrete Signaldarstellung]] vor $($Symboldauer $T = 1\ \rm µ s)$. |
* Für die Bitraten dieser beiden ersten Signale gilt jeweils $R_1 = R_2 = 1/T = \text{1 Mbit/s}$. Dagegen ist die Bitrate von $q_3(t)$ doppelt so groß, also $R_3 = \text{2 Mbit/s}$. | * Für die Bitraten dieser beiden ersten Signale gilt jeweils $R_1 = R_2 = 1/T = \text{1 Mbit/s}$. Dagegen ist die Bitrate von $q_3(t)$ doppelt so groß, also $R_3 = \text{2 Mbit/s}$. | ||
*Unten dargestellt ist das gemeinsame Zeitmultiplex–Ausgangssignal $q(t)$ mit der Gesamtbitrate $R = R_1 + R_2 + R_3 = \text{4 Mbit/s}$. Der Bezug zu den Eingangssignalen ist farblich gekennzeichnet. | *Unten dargestellt ist das gemeinsame Zeitmultiplex–Ausgangssignal $q(t)$ mit der Gesamtbitrate $R = R_1 + R_2 + R_3 = \text{4 Mbit/s}$. Der Bezug zu den Eingangssignalen ist farblich gekennzeichnet. | ||
Revision as of 10:41, 9 July 2020
Contents
- 1 # ÜBERBLICK ZUM ERSTEN HAUPTKAPITEL #
- 2 Betrachtetes Nachrichtenübertragungssystem
- 3 Anpassung an Übertragungskanal und Störspektrum
- 4 Bündelung von Kanälen – Frequenzmultiplex
- 5 Analoges Übertragungssystem vs. digitales Übertragungssystem
- 6 Zur Entwicklung der analogen Modulationsverfahren
- 7 Vorteile der digitalen Modulationsverfahren
- 8 Zeitmultiplexverfahren
- 9 Aufgaben zum Kapitel
# ÜBERBLICK ZUM ERSTEN HAUPTKAPITEL #
Dieses Buch behandelt mit Modulation und Demodulation zwei klassische und wichtige Verfahren der Nachrichtentechnik, die zum einen bereits eine sehr lange Tradition haben, sich aber andererseits stets weiter entwickeln.
Bevor in den folgenden Kapiteln die analoge Amplituden– und Winkelmodulation sowie die heute wichtigeren digitalen Modulationsverfahren im Detail beschrieben werden, sollen in diesem ersten Kapitel die für alle Systeme gleichermaßen gültigen Definitionen und Beschreibungsgrößen erläutert werden.
Dieses Kapitel behandelt im Einzelnen:
- die Zielsetzungen von Modulation und Demodulation,
- die Unterschiede und Gemeinsamkeiten von analogen und digitalen Modulationsverfahren,
- das Signal–zu–Stör–Leistungsverhältnis als ein sehr allgemeines Qualitätskriterium,
- die linearen und nichtlinearen Verzerrungen aufgrund von Modulation/Demodulation,
- die Degradation bei Vorhandensein stochastischer Störungen – zum Beispiel Rauschen,
- ein gemeinsames Modell zur Beschreibung von Amplituden– und Winkelmodulation,
- die Beschreibung durch das analytische Signal und das äquivalente Tiefpass–Signal.
Betrachtetes Nachrichtenübertragungssystem
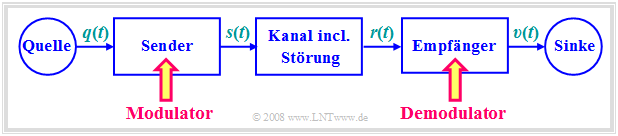
Im gesamten Buch „Modulationsverfahren” wird von dem hier dargestellten Blockschaltbild ausgegangen.
Das Übertragungsmedium (der physikalische Übertragungskanal) wird hier durch seinen Frequenzgang $H_{\rm K}(f)$ beschrieben. Betrachtet werden:
- elektrische Leitung (Koaxialkabel, Twisted Pair, usw.),
- Lichtwellenleiter (Multimode– bzw. Monomode–Glasfaser),
- Funkverbindungen (Richtfunk, Satellitenfunk, Mobilfunk, usw.).
Weiter ist anzumerken:
- Das zur Übertragung anstehende Quellensignal $q(t)$ sei ein Analogsignal, zum Beispiel Sprache, Musik oder der Ausgang einer (analogen) Kamera. Das zugehörige Spektrum $Q(f)$ sei auf den Frequenzbereich $|f| ≤ B_{\rm NF}$ begrenzt, wobei der Index für „Niederfrequenz” steht.
- Der mittlere Block in obigem Bild beinhaltet auch Störungen (Interferenzen, Übersprechen anderer Nutzer, Impulsstörungen durch Starkstromleitungen, etc.) und Rauschquellen wie Widerstands– und Halbleiterrauschen. Diese werden durch das Störleistungsdichtespektrum ${\it Φ}_n(f)$ erfasst.
- Aufgabe eines solchen Nachrichtenübertragungssystems ist es, die im Quellensignal $q(t)$ enthaltene Nachricht bzw. Information – man beachte die unterschiedliche Bedeutung dieser Größen – zur räumlich entfernten Sinke zu übertragen mit der Maßgabe, dass sich das Sinkensignal $v(t)$ „möglichst wenig” von $q(t)$ unterscheidet.
- Ein häufig auftretendes Problem ist, dass der Kanal für die direkte Übertragung des Quellensignals $q(t)$ ungeeignet ist, da dieses „ungünstige Frequenzen” beinhaltet. So kann ein Musiksignal mit Frequenzen bis ca. $\text{15 kHz}$ nicht direkt per Funk übertragen werden, da eine Funkausbreitung erst ab etwa $\text{100 kHz}$ möglich ist.
- Abhilfe schafft hier nur eine Signalumsetzung beim Sender, die man Modulation nennt. Das Ausgangssignal des Modulators wird im Folgenden einheitlich als Sendesignal $s(t)$ bezeichnet. Dieses liegt im allgemeinen bei höheren Frequenzen als das Quellensignal $q(t)$.
- Die Demodulation ist die Signalrücksetzung beim Empfänger, um aus dem hochfrequenten Empfangssignal $r(t)$ das niederfrequente Sinkensignal $v(t) ≈ q(t)$ zu gewinnen. Bei realem Kanal ist aufgrund des stets vorhandenen Rauschens $n(t)$ das Wunschergebnis $v(t) \equiv q(t)$ nicht möglich.
Anpassung an Übertragungskanal und Störspektrum
Die vorrangige Aufgabe der Modulation (im hier gemeinten Sinne) ist es, das Nachrichtensignal durch Zusetzen eines höherfrequenten Trägersignals mit der Trägerfrequenz $f_{\rm T}$ in eine andere Frequenzlage zu verschieben,
- mit günstigerem Frequenzgang $H_{\rm K}(f)$ und/oder
- mit günstigerem Störleistungsdichtespektrum ${\it Φ}_n(f)$.
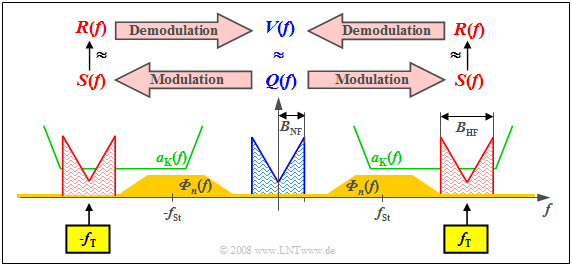
$\text{Beispiel 1:}$ Die Grafik zeigt in blau das niederfrequente Spektrum $Q(f)$ mit der Bandbreite $B_{\rm NF}$. Grün eingezeichnet ist der Dämpfungsverlauf $a_{\rm K}(f) = \ –\ln \ \vert H_{\rm K}(f) \vert $ des Kanals, der hier in einem ausreichend großen Frequenzbereich günstige Eigenschaften mit konstant geringer Dämpfung zeigt.
Ockerfarben sehen Sie das Störleistungsdichtespektrum ${\it Φ}_n(f)$, das wegen des thermischen Rauschens im gesamten Frequenzbereich nicht verschwindet und bei unserem konstruierten Beispiel um die Frequenz $f_{\rm St}$ aufgrund äußerer Störungen besonders große Werte annimmt.
Diese Randbedingungen machen deutlich:
- Man muss die Trägerfrequenz $f_{\rm T}$ in etwa so wählen wie eingezeichnet, damit $S(f)$ bestmöglich hinsichtlich Verzerrungen und Störungen/Rauschen übertragen werden kann. Es ergibt sich so ein Frequenzband ausreichender Qualität der Breite $B_{\rm HF} = 2 · B_{\rm NF}$.
- Diese Verschiebung des Quellensignal–Spektrums $Q(f)$ um die Trägerfrequenz $f_{\rm T}$ nach rechts – und aufgrund der systemtheoretischen Betrachtungsweise beidseitiger Frequenzen auch um den gleichen Abstand nach links – beschreibt die Modulation.
- Dagegen versteht man unter Demodulation die Signalumsetzung in Gegenrichtung. Ausgehend vom Empfangsspektrum $R(f)$, das sich vom Sendespektrum $S(f)$ aufgrund von Dämpfung und Rauschen zumindest geringfügig unterscheidet, kommt man zur Spektralfunktion $V(f) ≈ Q(f)$.
Weitere Gründe für Modulation/Demodulation werden in den nachfolgenden Abschnitten genannt.
Bündelung von Kanälen – Frequenzmultiplex
Ein weiterer Vorteil der Modulation mit einer harmonischen Schwingung als Trägersignal liegt darin, dass ein einziger Übertragungskanal ausreichender Bandbreite von mehreren Teilnehmern gleichzeitig genutzt werden kann. Man spricht dann
- von Frequenzmultiplex (FM) bzw. Frequency Division Multiplexing (FDM)
- oder auch von Frequency Division Multiple Access (FDMA).
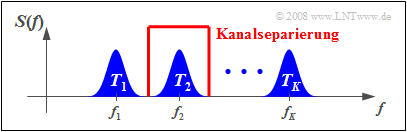
Die Grafik verdeutlicht den Sachverhalt. Über einen physikalischen Kanal entsprechender Bandbreite sollen $K$ Nachrichtensignale gleichzeitig übertragen werden. Die Teilkanäle sind hier mit $T_1$, ... , $T_K$ bezeichnet. Man geht folgendermaßen vor:
- Man moduliert die Quellensignale $q_1(t)$, $q_2(t)$, ... , $q_K(t)$ der Teilnehmer mit unterschiedlichen Trägerfrequenzen $f_1$, $f_2$, ... , $f_K$.
- Man fasst die Sendesignale $s_1(t)$, $s_2(t)$, ... , $s_K(t)$ zu einem Gesamtsignal $s(t)$ zusammen, so dass eine Mehrfachausnutzung der Übertragungseinrichtungen möglich ist.
- Zur Demodulation des Quellensignals $q_k(t)$ verwendet man die spezielle Trägerfrequenz $f_k$. Durch anschließende Filterung erreicht man $v_k(t) = q_k(t)$ (allerdings nur bei vernachlässigbaren Rauschstörungen). Man nennt den Vorgang Kanalseparierung.
$\text{Beispiel 2:}$ Die Frequenzmultiplextechnik wird schon seit vielen Jahrzehnten in der analogen TV– und Rundfunk–Übertragung angewandt.
- So können ausreichend viele Programme berücksichtigt werden, zum Beispiel im UHF–Band $($Frequenzen zwischen $\text{470 MHz}$ und $\text{850 MHz)}$ mehr als vierzig TV–Programme im Kanalabstand von $\text{8 MHz}$.
- Seit etwa 2004 wird die analoge TV–Übertragung in diesem Frequenzband allerdings mehr und mehr durch den neuen digitalen Video–Standard Digital Video Broadcast–Terrestrical (DVB–T) verdrängt, der ebenfalls FDMA nutzt.
$\text{Beispiel 3:}$
- In der optischen Übertragungstechnik bezeichnet man dieses FDMA–Verfahren als Wellenlängenmultiplex bzw. Wave–length Division Multiplex (WDM).
- Damit kann man derzeit (2005) über einen einzigen Lichtwellenleiter gleichzeitig $160$ Digitalsignale à $\text{10 Gbit/s}$ übertragen ⇒ Gesamtbitrate: $\text{1.6 Tbit/s}$.
Analoges Übertragungssystem vs. digitales Übertragungssystem
Für das gesamte Buch „Modulationsverfahren” wird vorausgesetzt, dass das Quellensignal $q(t)$ und das Sinkensignal $v(t)$ jeweils Analogsignale seien.
- Sie können also sowohl zeitkontinuierlich als auch wertkontinuierlich sein.
- Damit ist aber noch nicht festgelegt, ob die eigentliche Übertragung analog oder digital erfolgt.
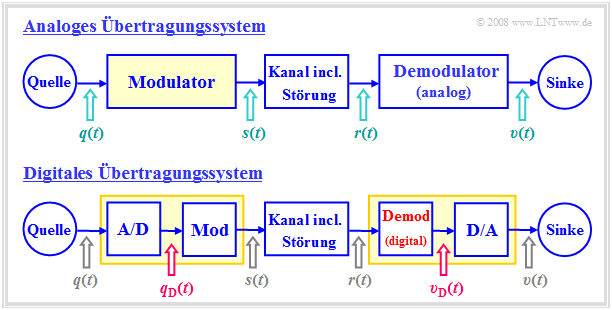
Die beiden Blockschaltbilder verdeutlichen die wesentlichen Unterschiede zwischen einem analogen und einem digitalen Nachrichtenübertragungssystem.
Man erkennt:
- Bei analoger Modulation ist das modulierende Signal $q(t)$ immer ein Analogsignal und damit sowohl wert– als auch zeitkontinuierlich.
- Dagegen ist bei digitaler Modulation das Eingangssignal $q_{\rm D}(t)$ des Modulators stets digital, also sowohl wertdiskret als auch zeitdiskret.
- Bei digitaler Modulation eines analogen Audio– oder Videosignals $q(t)$ muss dieses zunächst A/D–gewandelt werden: $q(t) \ \rightarrow \ q_{\rm D}(t)$.
- Man spricht von Pulscodemodulation. Diese erfordert sendeseitig folgende Maßnahmen: Abtastung – Quantisierung – (PCM–)Codierung.
- Funktional unterscheidet sich der Modulator des Digitalsystems $\rm (Mod)$ nicht vom Modulator des analogen Übertragungssystems.
- Die beiden Demodulatoren unterscheiden sich aber prinzipiell: Der obere liefert das Analogsignal $v(t)$, der untere das Digitalsignal $v_{\rm D}(t)$.
- Nach der digitalen Übertragung eines Analogsignals – beispielsweise Audio oder Video – muss somit noch eine D/A–Wandlung erfolgen.
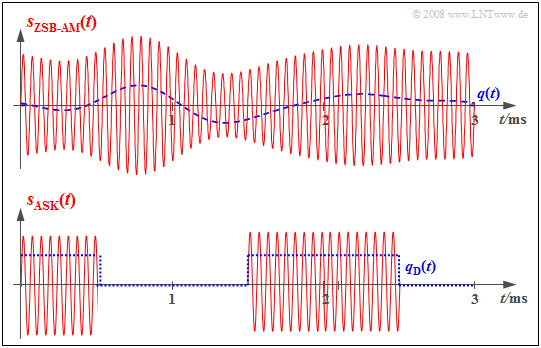
$\text{Beispiel 4:}$ Die beiden Grafiken zeigen die jeweiligen Eingangssignale (jeweils blau gestrichelt) und Ausgangssignale (durchgehend rot) des Modulators bei einem analogen und einem digitalen Übertragungssystem.
- Beim analogen Übertragungssystem (oben) steckt die Information über das analoge Quellensignal $q(t)$ direkt in der Amplitude (Hüllkurve) des modulierten Signals $s(t)$. Es handelt sich hierbei um das analoge Modulationsverfahren Zweiseitenband–Amplitudenmodulation mit Träger.
- Die untere Grafik bezieht sich auf Amplitude Shift Keying (ASK), die digitale Variante der Amplitudenmodulation. Hier ist das Modulatoreingangssignal $q_{\rm D}(t)$ digital und aus dem analogen Quellensignal $q(t)$ durch Abtastung, Quantisierung und PCM–Codierung entstanden.
- Das modulierte Signal $s(t)$ zeigt, dass der Modulator auch beim digitalen Übertragungssystem eine ähnliche Funktionalität aufweist wie beim (oberen) analogen Übertragungssystem.
Analoge Modulationsverfahren haben derzeit (2005) vor allem für die Verbreitung von Rundfunk– und Fernsehprogrammen noch eine gewisse Bedeutung, werden aber auch in diesem Bereich mehr und mehr durch entsprechende Digitalverfahren verdrängt. Trotzdem nehmen die Analogverfahren in diesem Buch einen breiteren Raum ein:
- Kapitel 2: Amplitudenmodulation und AM–Demodulation,
- Kapitel 3: Winkelmodulation und WM–Demodulation.
$\text{Die Gründe hierfür sind:}$
- Aufgrund der hohen Kosten bei der Umrüstung bestehender sowie der Einführung neuer Systeme werden auch für die Analogsysteme noch längere Laufzeiten prognostiziert.
- Viele Komponenten eines Analogsystems werden ebenso bei den digitalen Modulationsverfahren benötigt, zum Beispiel der in beiden Varianten verwendete Synchrondemodulator.
- Die typische Vorgehensweise bei der Untersuchung nachrichtentechnischer Aspekte lässt sich bei Analogsystemen umfassender – und oft auch verständlicher – erklären als bei Digitalsystemen.
Zur Entwicklung der analogen Modulationsverfahren
Es folgen einige Daten zur geschichtlichen Entwicklung der analogen Modulation. Meilensteine für die Entwicklung der analogen Modulationsverfahren auf Trägerfrequenzbasis waren:
- die Einführung des regulären Rundfunkdienstes (1923),
- der Beginn der Trägerfrequenztelefonie (1923),
- die Einführung des regulären Fernsehdienstes (1935),
- die erste Satellitenübertragung (1945),
- die Einführung des NTSC–Farbfernsehens (1953),
- die Einführung des PAL–Farbfernsehens (1967).
Voraussetzungen für diese Entwicklungen waren unter Anderem folgende Erfindungen in der Vergangenheit:
- 1861: die elektrische Übertragung von Sprache ⇒ Philip Reis,
- 1876: das erste kommerziell nutzbare Telefon ⇒ Alexander Graham Bell,
- 1884: die Entwicklung des Zeilenabtastverfahrens ⇒ Paul Julius Gottlieb Nipkow,
- 1887: die Entdeckung der elektromagnetischen Wellen ⇒ Heinrich Hertz,
- 1906: die Erfindung der Elektronenröhre ⇒ Robert von Lieben und Lee de Forest,
- 1948: die Erfindung des Transistors ⇒ William Bradford Shockley, Walter Houser Brattain und John Bardeen.
Vorteile der digitalen Modulationsverfahren
Die Vorteile der digitalen Modulationsverfahren sind vielfältig:
- Die Realisierung eines Digitalsystems kann ebenfalls digital erfolgen und die Schaltungen sind in hohem Maße integrierbar (VLSI – Very Large Scale Integration).
- Die Übertragungsqualität ist meist sehr gut, da sich (Rausch–)Störungen nur dann bemerkbar machen, wenn sie größer als ein vorgegebener Schwellenwert sind.
- Wegen der möglichen Signalregenerierung in regelmäßigen Abständen durch so genannte Regeneratoren können sehr große Entfernungen mit hinreichend guter Übertragungsqualität überbrückt werden.
- Die Datenübertragung – zum Beispiel zwischen Server und Client – bietet sich in digitaler Form an, da jedes Datensignal bereits digital ist. Analogsignale müssen vor der Übertragung digitalisiert werden.
- Durch die einheitliche Übertragung von Sprach–, Bild– und Datensignalen ist es möglich, ein gemeinsames und leistungsfähiges Netz für viele Telekommunikationsdienste aufzubauen.
- Es existieren einfache und sehr effiziente Verschlüsselungs– und Datensicherungsmechanismen für Digitalsignale, was eine wichtige Voraussetzung für sicherheitskritische Anwendungen ist.
- Bei einem Digitalsystem können – eventuell zusätzlich zu Frequenzmultiplex – auch die Vorteile von Zeitmultiplexverfahren genutzt werden, die nachfolgend beschrieben werden.
Alle in den letzten Jahren entwickelten Systeme sind digital, zum Beispiel:
- Compact Disc (CD) – digitales Speichermedium (Philips, 1982),
- Digital European Cordless Telephone (DECT) – schnurloses Telefon (1992),
- Global System for Mobile Communication (GSM) – europäisches Mobilfunksystem (1992),
- Integrated Services Digital Network (ISDN) – digitales Telefonnetz (in Europa 1993),
- Digital Audio Broadcast (DAB) – digitaler Rundfunk (2001),
- Digital Video Broadcast (DVB) – digitales Fernsehen (2002),
- Digital Subscriber Line (DSL) – schnelle Rechnerkopplung (2002),
- Universal Mobile Telephone System UMTS) – Mobilfunk der 3. Generation (2003),
- Long Term Evolution (LTE) – Mobilfunk der 4. Generation (2011).
Die Zahlen in Klammern geben jeweils die Jahreszahl des ersten Einsatzes an. Meistens hat es von der Erfindung über die Standardisierung bis hin zur Entwicklung eines einsatzfähigen Systems mehr als ein Jahrzehnt gedauert.
- In vierten Hauptkapitel dieses Buches sind die digitalen Modulationsverfahren zusammenfassend dargestellt.
- Eine detaillierte Beschreibung (Berechnung der Fehlerwahrscheinlichkeit, Aspekte der Systemoptimierung, usw.) finden Sie im Buch Digitalsignalübertragung.
Zeitmultiplexverfahren
Bei einem Digitalsystem kann zur gemeinsamen Nutzung eines Übertragungskanals durch mehrere Nutzer neben Frequenzmultiplex auch die Zeitmultiplextechnik eingesetzt werden. Die Grafik soll das Prinzip an einem Beispiel verdeutlichen:
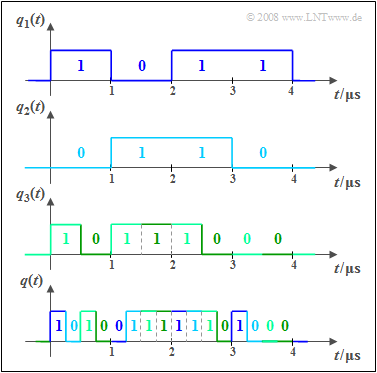
- Die Signale $q_1(t), q_2(t)$ und $q_3(t)$ sind binär und werden durch Amplitudenkoeffizienten $(0$ oder $1)$ vollständig beschrieben. Es liegt eine zeitdiskrete Signaldarstellung vor $($Symboldauer $T = 1\ \rm µ s)$.
- Für die Bitraten dieser beiden ersten Signale gilt jeweils $R_1 = R_2 = 1/T = \text{1 Mbit/s}$. Dagegen ist die Bitrate von $q_3(t)$ doppelt so groß, also $R_3 = \text{2 Mbit/s}$.
- Unten dargestellt ist das gemeinsame Zeitmultiplex–Ausgangssignal $q(t)$ mit der Gesamtbitrate $R = R_1 + R_2 + R_3 = \text{4 Mbit/s}$. Der Bezug zu den Eingangssignalen ist farblich gekennzeichnet.
- Nach der Übertragung von $q(t)$ über den physikalischen Kanal müssen die Teilsignale $v_1(t)$, ... , $v_3(t)$ beim Empfänger wieder getrennt werden. Man nennt diese Funktionseinheit den Demultiplexer.
- In der Praxis erfolgt das Multiplexen meist nicht bitweise, sondern den Teilnehmern werden in einem festen Raster Zeitschlitze zur Verfügung gestellt, in denen Bitrahmen übertragen werden.
Aufgaben zum Kapitel
Aufgabe 1.1: Multiplexing beim GSM–System