Difference between revisions of "Signal Representation/The Convolution Theorem and Operation"
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Aperiodic Signals - Impulses |
| − | |Vorherige Seite= | + | |Vorherige Seite=Fourier Transform Theorems |
| − | |Nächste Seite= | + | |Nächste Seite=Differences and Similarities of LP and BP Signals |
}} | }} | ||
| − | == | + | ==Convolution in Time Domain== |
<br> | <br> | ||
| − | + | The „convolution theorem” is one of the most important laws of the Fourier transform, to which an own subchapter is dedicated in this tutorial. | |
| − | + | We will first consider the convolution theorem in the time domain and assume that the spectra of two time functions $x_1(t)$ and $x_2(t)$ are known: | |
:$$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$ | :$$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$ | ||
| − | + | Then for the time function of the product $X_1(f) \cdot X_2(f)$ applies: | |
:$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | + | Here $\tau$ is a formal integration variable with the dimension of a time. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ The above connection of the time function $x_1(t)$ and $x_2(t)$ is called '''convolution''' and represents this functional connection with a star: |
:$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$ | :$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$ | ||
| − | + | Thus the above Fourier correspondence can be written as follows: | |
:$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$ | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$ | ||
| − | + | The [[Signal_Representation/The_Convolution_Theorem_and_Operation#Beweis_des_Faltungssatzes|Proof]] will be shown at the end of the chapter.}} | |
| − | '' | + | ''Remark'': The convolution is '''commutative''' ⇒ The order of the operands can be changed: ${ {x}}_{\rm{1}} ( t ) * { {x}}_{\rm{2}} (t ) ={ {x}}_{\rm{2}} ( t ) * { {x}}_{\rm{1}} (t ) $. |
| − | [[File:EN_Sig_T_3_4_S1.png|right|frame| | + | [[File:EN_Sig_T_3_4_S1.png|right|frame|On Calculation of Signal and Spectrum of LTI–Output]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ Every linear time-invariant (LTI) system can be described by the frequency response $H(f)$ as well as by the impulse response $h(t)$ where the relation between these two system quantities is also given by the Fourier transform. |
| − | + | If a signal $x(t)$ with the spectrum $X(f)$ is applied to the input, the spectrum of the output signal is: | |
:$$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$ | :$$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$ | ||
| − | + | It is possible to calculate the output signal in the time domain with the convolution theorem: | |
:$$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$ | :$$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$ | ||
| − | + | This equation shows again ''commutativity'' of the convolution operation. }} | |
| − | == | + | ==Convolution in the Frequency Domain== |
<br> | <br> | ||
| − | + | The duality between time and frequency domain also allows statements regarding the spectrum of the product signal: | |
:$$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$ | :$$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$ | ||
| − | + | This result can be proved similarly to the [[Signal_Representation/The_Convolution_Theorem_and_Operation#Beweis_des_Faltungssatzes|convolution in the time domain]] . However, the integration variable $\nu$ now has the dimension of a frequency. | |
| − | [[File:EN_Sig_T_3_4_S2.png|right|frame| | + | [[File:EN_Sig_T_3_4_S2.png|right|frame|Convolution in the Frequency Domain with the Example of DSB–AM]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ The [[Modulation_Methods/Zweiseitenband-Amplitudenmodulation#Beschreibung_im_Zeitbereich|Double-Sideband Amplitude Modulation]] (DSB-AM) without a carrier is described by the drawn graph. |
| − | * | + | *The time domain representation (blue) shows the modulated signal $s(t)$ as the product of the message signal $q(t)$ and the (normalized) carrier signal $z(t)$. |
| − | * | + | *According to the convolution theorem it follows for the frequency range (red) that the output spectrum $S(f)$ is equal to the convolution product of $Q(f)$ and $Z(f)$ .}} |
| − | == | + | ==Convolution of a Function With a Dirac Function== |
<br> | <br> | ||
| − | + | The convolution operation becomes very simple, if one of the two operands is a [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal#Diracfunktion_im_Frequenzbereich|Dirac function]] .This applies equally to the convolution in the time and frequency domain. | |
| − | + | We will consider the convolution of a function $x_1(t)$ with the function | |
:$$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$ | :$$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$ | ||
| − | + | For the spectral function of the signal $y(t) = x_1(t) \ast x_2(t)$ it follows: | |
:$$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$ | :$$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$ | ||
| − | + | The complex exponential function leads to a shift by $T$ ⇒ [[Signal_Representation/Fourier_Transform_Laws#Verschiebungssatz|Shifting Theorem]], the factor $\alpha$ to a damping $(\alpha < 1)$ or amplification $(\alpha > 1)$. | |
| − | + | From this follows: | |
:$$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$ | :$$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{In | + | $\text{In Words: }$ The convolution of any function with a Dirac function at $t = T$ results in the function shifted to the right by $T$ while the weighting of the Dirac function by the factor $\alpha$ has to be taken into account.}} |
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ A square wave signal $x(t)$ is delayed by an LTI-system by the delay time $\tau = 3\,\text{ ms}$ and attenuated by the factor $\alpha = 0.5$ . |
| − | [[File:P_ID522__Sig_T_3_4_S3_neu.png|center|frame| | + | [[File:P_ID522__Sig_T_3_4_S3_neu.png|center|frame|Convolution of a Rectangle Pulse with a Dirac Function]] |
| − | + | Shift and attenuation can be recognized by the output signal $y(t)$ as well as by the impulse response $h(t)$.}} | |
| − | == | + | ==Graphical Convolution== |
<br> | <br> | ||
| − | + | For the descriptions on this page the following convolution operation is assumed: | |
| − | [[File:P_ID2723__Sig_T_3_4_programm.png|right|frame| | + | [[File:P_ID2723__Sig_T_3_4_programm.png|right|frame|Screenshot of an older version of the $\rm LNTwww$–Applet „Convolution”:<br> $x_1(t)$ is denoted as $x(t)$ and $x_2(t)$ as $h(t)$ ]] |
:$$y(t) = x_1 (t) * x_2 (t) $$ | :$$y(t) = x_1 (t) * x_2 (t) $$ | ||
:$$\Rightarrow \hspace{0.3cm}y(t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | :$$\Rightarrow \hspace{0.3cm}y(t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | + | The solution of the convolution integral shall be done graphically. It is assumed that $x_1(t)$ and $x_2(t)$ are continuous time signals. | |
| − | + | Then the following steps are required: | |
| − | # | + | # The '''time variables''' of the two functions '''change'': <br> $x_1(t) \to x_1(\tau)$, $x_2(t) \to x_2(\tau)$. |
| − | # | + | # '''Mirroring the second function''': $x_2(\tau) \to x_2(-\tau)$. |
| − | # | + | # '''Shifting''' the '''mirrorred function''' by $t$ $x_2(-\tau) \to x_2(t-\tau)$. |
| − | # ''' | + | # '''Multiplication''' of both functions $x_1(\tau)$ and $x_2(t-\tau)$. |
| − | # '''Integration''' | + | # '''Integration''' over the product respective $\tau$ between the limits $-\infty$ to $+\infty$. |
| − | + | Since the convolution is commutative, instead of $x_2(\tau)$ also $x_1(\tau)$ can be mirrored. | |
<br clear=all> | <br clear=all> | ||
Die Thematik wird auch durch das (neuere) HTML 5–Applet [[Applets:Zur_Verdeutlichung_der_grafischen_Faltung|Zur Verdeutlichung der grafischen Faltung]] veranschaulicht. | Die Thematik wird auch durch das (neuere) HTML 5–Applet [[Applets:Zur_Verdeutlichung_der_grafischen_Faltung|Zur Verdeutlichung der grafischen Faltung]] veranschaulicht. | ||
| − | [[File:P_ID582__Sig_T_3_4_S4_neu.png|right|frame| | + | [[File:P_ID582__Sig_T_3_4_S4_neu.png|right|frame|Example of a Convolution: <br>Jump Function Convoluted With The Exponential Function]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ |
| − | + | The procedure for the graphic convolution is now explained with a detailed example: | |
| − | * | + | *At the input of a filter there is a jump function $x(t) = \gamma(t)$ . |
| − | * | + | *The impulse response of the RC low pass filter is $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/d}.$ |
| − | + | The graphic shows the red colored input signal $x(\tau)$, blue the impulse response $h(\tau)$ and grey the output signal $y(\tau)$. | |
| − | + | The time axis is already renamed to $\tau$. | |
| − | + | The output signal can be calculated using the following equation, for example: | |
:$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | :$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| Line 141: | Line 140: | ||
| − | == | + | ==Clear Interpretation of The Convolution== |
<br> | <br> | ||
Wir gehen von einer Impulsantwort $h(t)$ aus, die zunächst eine Millisekunde lang konstant ist und dann bis zur Zeit $t = 3 \,\text{ms}$ linear bis auf Null abfällt. | Wir gehen von einer Impulsantwort $h(t)$ aus, die zunächst eine Millisekunde lang konstant ist und dann bis zur Zeit $t = 3 \,\text{ms}$ linear bis auf Null abfällt. | ||
| Line 148: | Line 147: | ||
| − | [[File:P_ID524__Sig_T_3_4_S5_rah.png|right|frame| | + | [[File:P_ID524__Sig_T_3_4_S5_rah.png|right|frame|On a Clear Interpretation of The Convolution]] |
Wir betrachten nun das aus sieben verschieden gewichteten und verschobenen Diracimpulsen bestehende Eingangssignal | Wir betrachten nun das aus sieben verschieden gewichteten und verschobenen Diracimpulsen bestehende Eingangssignal | ||
| Line 170: | Line 169: | ||
| − | == | + | ==Proof of The Convolution Theorem== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| Line 184: | Line 183: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Proof: }$ |
Die Fourierintegrale der Funktionen $x_1(t)$ und $x_2(t)$ lauten mit veränderten Integrationsvariablen: | Die Fourierintegrale der Funktionen $x_1(t)$ und $x_2(t)$ lauten mit veränderten Integrationsvariablen: | ||
| Line 212: | Line 211: | ||
| − | == | + | ==Exercises for the Chapter== |
<br> | <br> | ||
[[Aufgaben:Exercise_3.7:_Carrier_Recovery|Exercise 3.7: Carrier Recovery]] | [[Aufgaben:Exercise_3.7:_Carrier_Recovery|Exercise 3.7: Carrier Recovery]] | ||
Revision as of 23:42, 18 November 2020
Contents
Convolution in Time Domain
The „convolution theorem” is one of the most important laws of the Fourier transform, to which an own subchapter is dedicated in this tutorial.
We will first consider the convolution theorem in the time domain and assume that the spectra of two time functions $x_1(t)$ and $x_2(t)$ are known:
- $$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$
Then for the time function of the product $X_1(f) \cdot X_2(f)$ applies:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
Here $\tau$ is a formal integration variable with the dimension of a time.
$\text{Definition:}$ The above connection of the time function $x_1(t)$ and $x_2(t)$ is called convolution and represents this functional connection with a star:
- $$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$
Thus the above Fourier correspondence can be written as follows:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$
The Proof will be shown at the end of the chapter.
Remark: The convolution is commutative ⇒ The order of the operands can be changed: ${ {x}}_{\rm{1}} ( t ) * { {x}}_{\rm{2}} (t ) ={ {x}}_{\rm{2}} ( t ) * { {x}}_{\rm{1}} (t ) $.
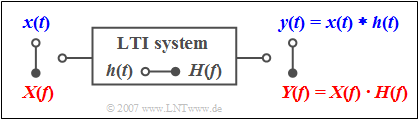
$\text{Example 1:}$ Every linear time-invariant (LTI) system can be described by the frequency response $H(f)$ as well as by the impulse response $h(t)$ where the relation between these two system quantities is also given by the Fourier transform.
If a signal $x(t)$ with the spectrum $X(f)$ is applied to the input, the spectrum of the output signal is:
- $$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$
It is possible to calculate the output signal in the time domain with the convolution theorem:
- $$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$
This equation shows again commutativity of the convolution operation.
Convolution in the Frequency Domain
The duality between time and frequency domain also allows statements regarding the spectrum of the product signal:
- $$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$
This result can be proved similarly to the convolution in the time domain . However, the integration variable $\nu$ now has the dimension of a frequency.
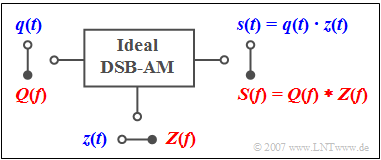
$\text{Example 2:}$ The Double-Sideband Amplitude Modulation (DSB-AM) without a carrier is described by the drawn graph.
- The time domain representation (blue) shows the modulated signal $s(t)$ as the product of the message signal $q(t)$ and the (normalized) carrier signal $z(t)$.
- According to the convolution theorem it follows for the frequency range (red) that the output spectrum $S(f)$ is equal to the convolution product of $Q(f)$ and $Z(f)$ .
Convolution of a Function With a Dirac Function
The convolution operation becomes very simple, if one of the two operands is a Dirac function .This applies equally to the convolution in the time and frequency domain.
We will consider the convolution of a function $x_1(t)$ with the function
- $$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$
For the spectral function of the signal $y(t) = x_1(t) \ast x_2(t)$ it follows:
- $$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$
The complex exponential function leads to a shift by $T$ ⇒ Shifting Theorem, the factor $\alpha$ to a damping $(\alpha < 1)$ or amplification $(\alpha > 1)$.
From this follows:
- $$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$
$\text{In Words: }$ The convolution of any function with a Dirac function at $t = T$ results in the function shifted to the right by $T$ while the weighting of the Dirac function by the factor $\alpha$ has to be taken into account.
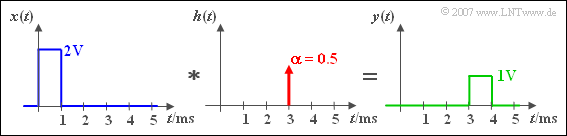
$\text{Example 3:}$ A square wave signal $x(t)$ is delayed by an LTI-system by the delay time $\tau = 3\,\text{ ms}$ and attenuated by the factor $\alpha = 0.5$ .
Shift and attenuation can be recognized by the output signal $y(t)$ as well as by the impulse response $h(t)$.
Graphical Convolution
For the descriptions on this page the following convolution operation is assumed:
- $$y(t) = x_1 (t) * x_2 (t) $$
- $$\Rightarrow \hspace{0.3cm}y(t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
The solution of the convolution integral shall be done graphically. It is assumed that $x_1(t)$ and $x_2(t)$ are continuous time signals.
Then the following steps are required:
- The time variables' of the two functions change:
$x_1(t) \to x_1(\tau)$, $x_2(t) \to x_2(\tau)$. - Mirroring the second function: $x_2(\tau) \to x_2(-\tau)$.
- Shifting the mirrorred function by $t$ $x_2(-\tau) \to x_2(t-\tau)$.
- Multiplication of both functions $x_1(\tau)$ and $x_2(t-\tau)$.
- Integration over the product respective $\tau$ between the limits $-\infty$ to $+\infty$.
Since the convolution is commutative, instead of $x_2(\tau)$ also $x_1(\tau)$ can be mirrored.
Die Thematik wird auch durch das (neuere) HTML 5–Applet Zur Verdeutlichung der grafischen Faltung veranschaulicht.
$\text{Example 4:}$ The procedure for the graphic convolution is now explained with a detailed example:
- At the input of a filter there is a jump function $x(t) = \gamma(t)$ .
- The impulse response of the RC low pass filter is $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/d}.$
The graphic shows the red colored input signal $x(\tau)$, blue the impulse response $h(\tau)$ and grey the output signal $y(\tau)$.
The time axis is already renamed to $\tau$.
The output signal can be calculated using the following equation, for example:
- $$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
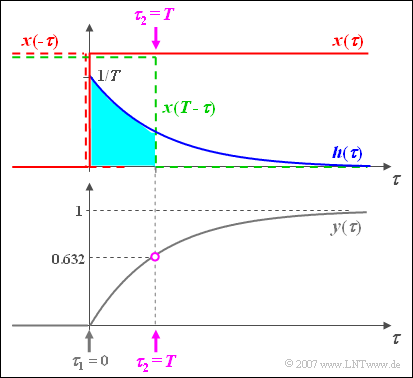
Noch einige Anmerkungen zur grafischen Faltung:
- Der Ausgangswert bei $t = 0$ ergibt sich, indem man das Eingangssignal $x(\tau)$ spiegelt, dieses gespiegelte Signal $x(-\tau)$ mit der Impulsantwort $h(\tau)$ multipliziert und darüber integriert.
- Da es hier kein Zeitintervall gibt, bei dem sowohl die blaue Kurve $h(\tau)$ und gleichzeitig auch die rot gestrichelte Spiegelung $x(-\tau)$ ungleich Null ist, folgt daraus $y(t=0)=0$.
- Für jeden anderen Zeitpunkt $t$ muss das Eingangssignal verschoben werden ⇒ $x(t-\tau)$, beispielsweise entsprechend der grün gestrichelten Kurve für $t=T$.
- Da in diesem Beispiel auch $x(t-\tau)$ nur $0$ und $1$ sein kann, wird die Integration $($allgemein von $\tau_1$ bis $\tau_2)$ sehr einfach und man erhält hier mit $\tau_1 = 0$ und $\tau_2 = t$ :
- $$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$
Die Skizze gilt für $t=T$ und führt zum Ausgangswert $y(t=T) = 1 – 1/\text{e} \approx 0.632$.
Clear Interpretation of The Convolution
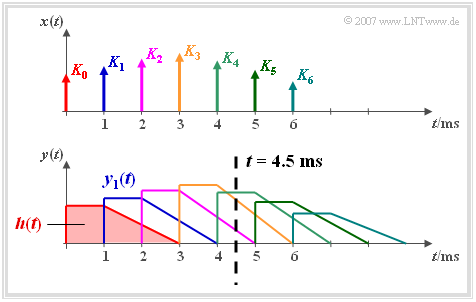
Wir gehen von einer Impulsantwort $h(t)$ aus, die zunächst eine Millisekunde lang konstant ist und dann bis zur Zeit $t = 3 \,\text{ms}$ linear bis auf Null abfällt.
- Legt man an den Eingang dieses Tiefpassfilters einen Diracimpuls $K_0 \cdot \delta(t)$ an, so ist das Ausgangssignal $y(t)$ formgleich mit der Impulsantwort $h(t)$. Der Sachverhalt ist im Bild rot dargestellt.
- Ein um $T= 1 \,\text{ms}$ späterer Diracimpuls mit Gewicht $K_1 > K_0$ hat das blau gezeichnete Ausgangssignal $y_1(t)$ zur Folge, das gegenüber dem roten Signal verzögert und in der Amplitude vergrößert ist.
Wir betrachten nun das aus sieben verschieden gewichteten und verschobenen Diracimpulsen bestehende Eingangssignal
- $$x( t ) = \sum\limits_{n = 0}^6 {K_n \cdot \delta ( {t - n \cdot T} ),}$$
das als zeitdiskrete Näherung eines zeitkontinuierlichen Signals aufgefasst werden kann.
- Das Signal am Ausgang des linearen Systems ist die Summe der sieben im Bild verschiedenfarbig markierten Teilsignale:
- $$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$
- Wir betrachten nun beispielhaft den Signalwert zum Zeitpunkt $t = 4.5T$ (siehe Strichpunktierung):
- $$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$
Der Signalwert $y(t=4.5T)$ wird somit nur durch die Eingangssignalwerte $K_2$, $K_3$ und $K_4$ bestimmt, und zwar ist der Einfluss
- von $K_4$ wegen $h(0.5T) = 1$ am stärksten,
- von $K_3$ wegen $h(1.5T) = 0.75$ weniger stark,
- von $K_2$ wegen $h(2.5T) = 0.25$ am geringsten.
Proof of The Convolution Theorem
$\text{Definition: }$ Man nennt die folgende Verknüpfung der Zeitfunktionen $x_1(t)$ und $x_2(t)$ die Faltung und stellt diesen Funktionalzusammenhang mit einem Stern dar:
- $$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
Daraus ergibt sich die folgende Fourierkorrespondenz:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$
$\text{Proof: }$ Die Fourierintegrale der Funktionen $x_1(t)$ und $x_2(t)$ lauten mit veränderten Integrationsvariablen:
- $$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\tau }\hspace{0.1cm} {\rm{d } }\tau{\rm{,} }$$
- $$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t'} ) } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft\hspace{0.05cm}'}\hspace{0.1cm} {\rm{d} }t\hspace{0.05cm}'{\rm{.} }$$
- Bildet man das Produkt der Spektralfunktionen, so erhält man:
- $$X_1 (f) \cdot X_2 (f) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {x_1 ( \tau ) \hspace{0.05 cm}\cdot } }\hspace{0.05 cm} x_2 ( {t\hspace{0.05cm}'} ) \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\left( {\tau + t\hspace{0.05cm}'} \right) }\hspace{0.1cm} {\rm d} \tau \hspace{0.1cm}{\rm d}t\hspace{0.05cm}'{\rm{.} }$$
- Mit der Substitution $t = \tau + t\hspace{0.05cm}'$ ergibt sich:
- $$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d } } }\tau \right] } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft}\hspace{0.1cm} {\rm{d} }t{\rm{.} }$$
- In dieser Gleichung ist bereits berücksichtigt, dass die Exponentialfunktion unabhängig von der inneren Integrationsvariablen $τ$ ist und deshalb nur als Faktor des inneren Integrals fungiert.
- Bezeichnen wir nun das Produkt der beiden Spektren mit $P(f)$ und die dazugehörige Zeitfunktion mit $p(t)$, so lautet das entsprechende Fourierintegral:
- $$P(f) = X_1 ( f ) \cdot X_2 ( f ) =\int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft} \hspace{0.1cm}{\rm{d} }t{\rm{.} }$$
- Ein Koeffizientenvergleich der beiden Integrale zeigt, dass folgender Zusammenhang gelten muss:
- $$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d } }\tau{\rm{.} }$$
Exercises for the Chapter
Exercise 3.7: Carrier Recovery
Exercise 3.7Z: Square Wave With Echo
Exercise 3.8: Triple Convolution
Exercise 3.8Z:Convolution of Two Rectangles
Exercise 3.9: Convolution of Rectangle and Gaussian Pulse
Exercise 3.9Z: Convolution of Gaussian Pulses