Difference between revisions of "Aufgaben:Exercise 4.3: Subcarrier Mapping"
From LNTwww
m (Text replacement - "Mobile Kommunikation/Die Anwendung von OFDMA und SC-FDMA in LTE" to "Mobile_Communications/The_Application_of_OFDMA_and_SC-FDMA_in_LTE") |
|||
| Line 5: | Line 5: | ||
| − | [[File:EN_Mob_A_4_3.png|right|frame|Two SC | + | [[File:EN_Mob_A_4_3.png|right|frame|Two SC–FDMA arrangements]] |
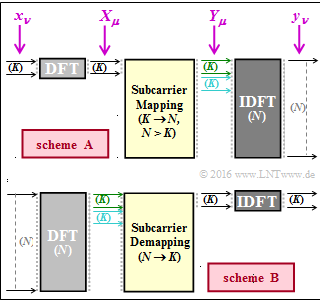
| − | The diagram shows two transmission schemes that play a role in connection with | + | The diagram shows two transmission schemes that play a role in connection with Long Term Evolution $\rm (LTE)$. These block diagrams are referred here neutrally as "arrangement $\rm A$&" or "arrangement $\rm B$". |
* The light grey blocks represent the transition from the time to the frequency domain. | * The light grey blocks represent the transition from the time to the frequency domain. | ||
* The dark grey blocks represent the transition from the frequency to the time domain. | * The dark grey blocks represent the transition from the frequency to the time domain. | ||
| Line 13: | Line 13: | ||
We refer here to the following links: | We refer here to the following links: | ||
| − | * [[Signal_Representation/Discrete_Fourier_Transform_(DFT)#Von_der_kontinuierlichen_zur_diskreten_Fouriertransformation|Diskrete Fouriertransformation]] ⇒ | + | * [[Signal_Representation/Discrete_Fourier_Transform_(DFT)#Von_der_kontinuierlichen_zur_diskreten_Fouriertransformation|Diskrete Fouriertransformation]] ⇒ $\rm DFT$ , |
| − | * [[Signal_Representation/Discrete_Fourier_Transform_(DFT)#Inverse_Diskrete_Fouriertransformation|Inverse Diskrete Fouriertransformation]] ⇒ | + | * [[Signal_Representation/Discrete_Fourier_Transform_(DFT)#Inverse_Diskrete_Fouriertransformation|Inverse Diskrete Fouriertransformation]] ⇒ $\rm IDFT$ . |
Revision as of 15:56, 2 February 2021
The diagram shows two transmission schemes that play a role in connection with Long Term Evolution $\rm (LTE)$. These block diagrams are referred here neutrally as "arrangement $\rm A$&" or "arrangement $\rm B$".
- The light grey blocks represent the transition from the time to the frequency domain.
- The dark grey blocks represent the transition from the frequency to the time domain.
We refer here to the following links:
- Diskrete Fouriertransformation ⇒ $\rm DFT$ ,
- Inverse Diskrete Fouriertransformation ⇒ $\rm IDFT$ .
Für die Stützstellenanzahl von DFT und IDFT werden mit $K = 12$ und $N = 1024$ realistische Zahlenwerte angenommen.
- Der Wert $K = 12$ ergibt sich aus der Tatsache, dass durch das Subcarrier–Mapping die Symbole auf eine gewisse Bandbreite „gemappt” werden. Der kleinste adressierbare Block ist bei LTE $180 \ \rm kHz$. Mit dem Unterträgerabstand von $15 \ \rm kHz$ ergibt sich $K = 12$.
- Mit der Stützstellenanzahl $N$ der IDFT $($bei Anordnung $\rm A)$ können somit bis zu $J = N/K$ Nutzer gleichzeitig bedient werden. Für das Subcarrier–Mapping gibt es mit DFDMA, IFDMA und LFDMA drei verschiedene Ansätze.
- Die beiden ersten Nutzer sind in der Grafik grün bzw. türkis eingezeichnet. In der Teilaufgabe (5) sollen Sie entscheiden, ob die Skizze für DFDMA, IFDMA oder LFDMA gilt.
Hinweis:
- Die Aufgabe gehört zum Kapitel Anwendung von OFDMA und SC-FDMA in LTE.
Fragebogen
Musterlösung
(1) Richtig ist der Lösungsvorschlag 2:
- Beide Anordnungen zeigen Single Carrier Frequency Division Multiple Access (SC–FDMA), erkennbar an den DFT– und IDFT–Blöcken.
- Der Vorteil gegenüber Orthogonal Frequency Division Multiple–Access (OFDMA) ist das günstigere Peak–to–Average Power–Ratio (PAPR).
- Ein großes PAPR führt dazu, dass man die Verstärker unterhalb der Sättigungsgrenze und damit bei schlechterem Wirkungsgrad betreiben muss, um zu starke Signalverzerrungen zu verhindern.
- Ein niedrigeres PAPR bedeutet gleichzeitig eine längere Batterielaufzeit, ein für Smartphones äußerst wichtiges Kriterium.
- Deshalb wird SC–FDMA im LTE–Uplink eingesetzt. Für den Downlink ist der hier genannte Aspekt weniger bedeutend.
(2) Richtig sind die Lösungsvorschläge 1 und 2:
- Während bei OFDMA die zu übertragenden Datensymbole direkt die verschiedenen Unterträger erzeugen, wird bei SC–FDMA ein Block von Datensymbolen mittels DFT zuerst in den Frequenzbereich transformiert.
- Um mehrere Nutzer übertragen zu können, muss $N > K$ gelten. Ein Eingangsblock eines Nutzers besteht somit aus $K$ Bit. Damit ist offensichtlich, dass die Anordnung $\rm A$ für den Sender gilt.
- Die Anordnung $\rm B$ beschreibt dagegen den Empfänger des LTE–Uplinks und nicht den Sender.
(3) Beide Aussagen sind zutreffend:
- Die Maßnahmen sind erforderlich, um einen kontinuierlichen Bitstrom am Sender verarbeiten zu können bzw. auch beim Empfänger einen kontinuierlichen Bitstrom zu gewährleisten.
(4) Die DFT erzeugt aus $K$ Eingangswerten ebenfalls $K$ Spektralwerte.
- Durch das Subcarrier–Mapping ändert sich dadurch nichts.
- Durch weitere Nutzer werden ebenfalls jeweils $K$ (Bit) der insgesamt $N$ (Bit) belegt.
- Damit können $J = N/K = 1024/12 = 85.333$ ⇒ $J \ \underline{= 85}$ Nutzer versorgt werden.
(5) Richtig ist der Lösungsvorschlag 3:
- Die Grafik entspricht der derzeitigen 3gpp–Spezifikation, die Localized Mapping vorsieht.
- Hierbei werden die $K$ Modulationssymbole benachbarten Unterträgern zugeordnet.
(6) Richtig sind die Lösungsvorschläge 2 und 3:
- Die Realisierung von DFT bzw. IDFT als (inverse) Fast Fourier Transform ist nur möglich, wenn die Stützstellenzahl eine Zweierpotenz ist.
- Also zum Beispiel für $N = 1024$, nicht aber für $K = 12$.