Difference between revisions of "Applets:Capacity of Memoryless Digital Channels"
| Line 282: | Line 282: | ||
*First, select the number $(1,\ 2, \text{...} \ )$ of the task to be processed. The number "$0$" corresponds to a "Reset": Same setting as at program start. | *First, select the number $(1,\ 2, \text{...} \ )$ of the task to be processed. The number "$0$" corresponds to a "Reset": Same setting as at program start. | ||
*A task description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution". | *A task description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution". | ||
| + | *Source symbols are denoted by uppercase letters (binary: $\rm A$, $\rm B$), sink symbols by lowercase letters ($\rm a$, $\rm b$). Error-free transmission: $\rm A \rightarrow a$. | ||
*For all entropy values, the unit "bit/use" would have to be added. | *For all entropy values, the unit "bit/use" would have to be added. | ||
Deutsch: | Deutsch: | ||
| − | |||
*Wählen Sie zunächst die Nummer ($1$, $2$, ... ) der zu bearbeitenden Aufgabe. Die Nummer $0$ entspricht einem „Reset”: Einstellung wie beim Programmstart. | *Wählen Sie zunächst die Nummer ($1$, $2$, ... ) der zu bearbeitenden Aufgabe. Die Nummer $0$ entspricht einem „Reset”: Einstellung wie beim Programmstart. | ||
*Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. Lösung nach Drücken von „Musterlösung”. | *Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. Lösung nach Drücken von „Musterlösung”. | ||
| + | *Die Quellensymbole werden mit Großbuchstaben bezeichnet (binär: $\rm A$, $\rm B$), die Sinkenssymbole mit Kleinbuchstaben ($\rm a$, $\rm b$). Fehlerfreie Übertragung: $\rm A \rightarrow a$. | ||
*Bei allen Entropiewerten müsste die Einheit „bit/use” hizugefügt werden. | *Bei allen Entropiewerten müsste die Einheit „bit/use” hizugefügt werden. | ||
<br clear=all> | <br clear=all> | ||
| Line 314: | Line 315: | ||
:* Due to the symmetry of the BSC model equally probable symbols $(p_{\rm A} = p_{\rm B} = 0.5)$ lead to the optimum ⇒ $C_{\rm BSC}=0.531$. | :* Due to the symmetry of the BSC model equally probable symbols $(p_{\rm A} = p_{\rm B} = 0.5)$ lead to the optimum ⇒ $C_{\rm BSC}=0.531$. | ||
:* The best is the "ideal channel" $(p_{\rm b \vert A} = p_{\rm a \vert B} = 0)$ ⇒ $C_{\rm BSC}=1$. The worst BSC channel results with $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.5$ ⇒ $C_{\rm BSC}=0$. | :* The best is the "ideal channel" $(p_{\rm b \vert A} = p_{\rm a \vert B} = 0)$ ⇒ $C_{\rm BSC}=1$. The worst BSC channel results with $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.5$ ⇒ $C_{\rm BSC}=0$. | ||
| − | :* But also with $p_{\rm b \vert A} = p_{\rm a \vert B} = 1$ we get $C_{\rm BSC}=1$. Here all symbols are inverted, which is information theoretically the same as $\langle Y_n \rangle | + | :* But also with $p_{\rm b \vert A} = p_{\rm a \vert B} = 1$ we get $C_{\rm BSC}=1$. Here all symbols are inverted, which is information theoretically the same as $\langle Y_n \rangle \equiv \langle X_n \rangle$. |
| Line 323: | Line 324: | ||
:* Aufgrund der Symmetrie des BSC–Modells führen gleichwahrscheinliche Symbole $(p_{\rm A} = p_{\rm B} = 0.5)$ zum Optimum ⇒ $C_{\rm BSC}=0.531$. | :* Aufgrund der Symmetrie des BSC–Modells führen gleichwahrscheinliche Symbole $(p_{\rm A} = p_{\rm B} = 0.5)$ zum Optimum ⇒ $C_{\rm BSC}=0.531$. | ||
:* Am besten ist der ideale Kanal $(p_{\rm b \vert A} = p_{\rm a \vert B} = 0)$ ⇒ $C_{\rm BSC}=1$. Der schlechteste BSC–Kanal liegt durch $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.5$ fest ⇒ $C_{\rm BSC}=0$. | :* Am besten ist der ideale Kanal $(p_{\rm b \vert A} = p_{\rm a \vert B} = 0)$ ⇒ $C_{\rm BSC}=1$. Der schlechteste BSC–Kanal liegt durch $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.5$ fest ⇒ $C_{\rm BSC}=0$. | ||
| − | :* Aber auch mit $p_{\rm b \vert A} = p_{\rm a \vert B} = 1$ ergibt sich $C_{\rm BSC}=1$. Hier werden alle Symbole invertiert, was informationstheoretisch das Gleiche ist wie $\langle Y_n \rangle | + | :* Aber auch mit $p_{\rm b \vert A} = p_{\rm a \vert B} = 1$ ergibt sich $C_{\rm BSC}=1$. Hier werden alle Symbole invertiert, was informationstheoretisch das Gleiche ist wie $\langle Y_n \rangle \equiv \langle X_n \rangle$. |
{{BlueBox|TEXT= | {{BlueBox|TEXT= | ||
| − | '''(3)''' Let $p_{\rm A} = p_{\rm B} = 0.5$, $p_{\rm b \vert A} = 0.05$ and $ p_{\rm a \vert B} = 0.4$. Interpret the results in comparison to the experiment | + | '''(3)''' Let $p_{\rm A} = p_{\rm B} = 0.5$, $p_{\rm b \vert A} = 0.05$ and $ p_{\rm a \vert B} = 0.4$. Interpret the results in comparison to the experiment $(1)$ and to the $\text{example 2}$ in the theory section.}} |
| − | :* Unlike the experiment | + | :* Unlike the experiment $(1)$ no BSC channel is present here. Rather, the channel considered here is asymmetric: $p_{\rm b \vert A} \ne p_{\rm a \vert B}$. |
:* According to $\text{Example 2}$ holds for $p_{\rm A} = 0.1,\ p_{\rm B} = 0.9$: $H(X)= 0.469$, $H(Y)= 0.994$, $H(X \vert Y)=0.377$, $H(Y \vert X)=0.902$, $I(X;\vert Y)=0.092$. | :* According to $\text{Example 2}$ holds for $p_{\rm A} = 0.1,\ p_{\rm B} = 0.9$: $H(X)= 0.469$, $H(Y)= 0.994$, $H(X \vert Y)=0.377$, $H(Y \vert X)=0.902$, $I(X;\vert Y)=0.092$. | ||
:* Now holds $p_{\rm A} = p_{\rm B} = 0.5$ and we get $H(X)=1,000$, $H(Y)=0.910$, $H(X \vert Y)=0.719$, $H(Y \vert X)=0.629$, $I(X;\ Y)=0.281$. | :* Now holds $p_{\rm A} = p_{\rm B} = 0.5$ and we get $H(X)=1,000$, $H(Y)=0.910$, $H(X \vert Y)=0.719$, $H(Y \vert X)=0.629$, $I(X;\ Y)=0.281$. | ||
| Line 347: | Line 348: | ||
:* The joint probabilities are $p_{\rm Aa} =0.475$, $p_{\rm Ab} =0.025$, $p_{\rm Ba} =0.200$, $p_{\rm Bb} =0.300$. Simulation: Approximation by relative frequencies: | :* The joint probabilities are $p_{\rm Aa} =0.475$, $p_{\rm Ab} =0.025$, $p_{\rm Ba} =0.200$, $p_{\rm Bb} =0.300$. Simulation: Approximation by relative frequencies: | ||
| − | :* For example, for $N=10000$: $h_{\rm Aa} =0.4778$, $h_{\rm Ab} =0.0264$, $h_{\rm Ba} =0.2039$, $h_{\rm Bb} =0.2919$. After pressing | + | :* For example, for $N=10000$: $h_{\rm Aa} =0.4778$, $h_{\rm Ab} =0.0264$, $h_{\rm Ba} =0.2039$, $h_{\rm Bb} =0.2919$. After pressing "New sequence" slightly different values. |
:* For all subsequent calculations, no principal difference between theory and simulation, except $p \to h$. Examples: | :* For all subsequent calculations, no principal difference between theory and simulation, except $p \to h$. Examples: | ||
:* $p_{\rm A} = 0.5 \to h_{\rm A}=h_{\rm Aa} + h_{\rm Ab} =0.5042$, $p_b = 0.325 \to h_{\rm b}=h_{\rm Ab} + h_{\rm Bb} =0. 318$, $p_{b|A} = 0.05 \to h_{\rm b|A}=h_{\rm Ab}/h_{\rm A} =0.0264/0.5042= 0.0524$, | :* $p_{\rm A} = 0.5 \to h_{\rm A}=h_{\rm Aa} + h_{\rm Ab} =0.5042$, $p_b = 0.325 \to h_{\rm b}=h_{\rm Ab} + h_{\rm Bb} =0. 318$, $p_{b|A} = 0.05 \to h_{\rm b|A}=h_{\rm Ab}/h_{\rm A} =0.0264/0.5042= 0.0524$, | ||
:* $p_{\rm A|b} = 0.0769 \to h_{\rm A|b}=h_{\rm Ab}/h_{\rm b} =0.0264/0.318= 0.0830$. Thus, this simulation yields $I_{\rm Sim}(X;\ Y)=0.269$ instead of $I(X;\ Y)=0.281$. | :* $p_{\rm A|b} = 0.0769 \to h_{\rm A|b}=h_{\rm Ab}/h_{\rm b} =0.0264/0.318= 0.0830$. Thus, this simulation yields $I_{\rm Sim}(X;\ Y)=0.269$ instead of $I(X;\ Y)=0.281$. | ||
| − | + | ===Dum=== | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
'''(4)''' Es gelte weiter $p_{\rm A} = p_{\rm B}$, $p_{\rm b \vert A} = 0.05$, $ p_{\rm a \vert B} = 0.4$. Welche Unterschiede erkennen Sie hinsichtlich analytischer Berechnung und „Simulation” $(N=10000)$.}} | '''(4)''' Es gelte weiter $p_{\rm A} = p_{\rm B}$, $p_{\rm b \vert A} = 0.05$, $ p_{\rm a \vert B} = 0.4$. Welche Unterschiede erkennen Sie hinsichtlich analytischer Berechnung und „Simulation” $(N=10000)$.}} | ||
Revision as of 18:12, 22 March 2021
Open Applet in new Tab Deutsche Version Öffnen
Contents
Applet Description
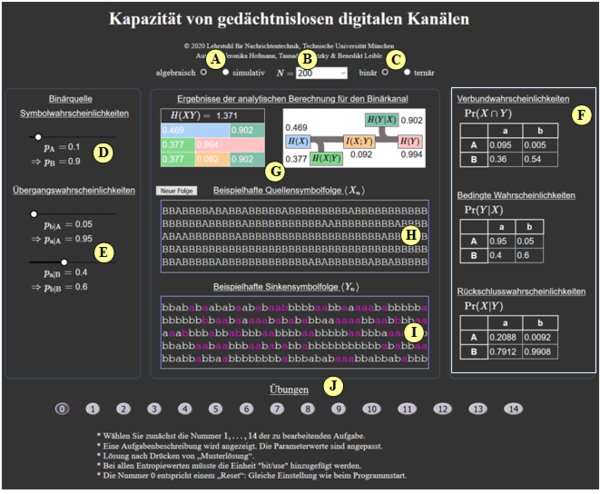
In diesem Applet werden binäre $(M=2)$ und ternäre $(M=3)$ Kanalmodelle ohne Gedächtnis betrachtet mit jeweils $M$ Eingängen $X$ und $M$ Ausgängen $Y$. Ein solches Nachrichtensystem ist durch die Wahrscheinlichkeitsfunktion $P_X(X)$ und die Matrix $P_{\hspace{0.01cm}Y\hspace{0.03cm} \vert \hspace{0.01cm}X}(Y\hspace{0.03cm} \vert \hspace{0.03cm} X)$ der Übergangswahrscheinlichkeiten vollständig bestimmt.
Für diese binären bzw. ternären Systeme werden folgende informationstheoretische Beschreibungsgrößen hergeleitet und verdeutlicht:
- die Quellenentropie $H(X)$ und die Sinkenentropie $H(Y)$,
- die Äquivokation („Rückschlussentropie”) $H(X|Y)$ und die Irrelevanz („Streuentropie”) $H(Y|X)$,
- die Verbundentropie $H(XY)$ sowie die Transinformation (englisch: Mutual Information) $I(X; Y)$,
- die Kanalkapazität als die entscheidende Kenngröße digitaler Kanalmodelle ohne Gedächtnis:
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
Diese informationstheoretische Größen können sowohl in analytisch–geschlossener Form berechnet oder durch Auswertung von Quellen– und Sinkensymbolfolge simulativ ermittelt werden.
Theoretical Background
Zugrunde liegendes Modell der Digitalsignalübertragung
Die Menge der möglichen Quellensymbole wird durch die diskrete Zufallsgröße $X$ charakterisiert.
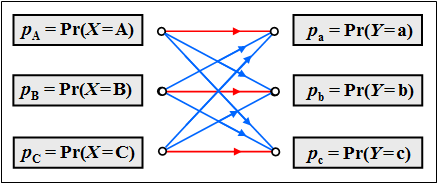
- Im binären Fall ⇒ $M_X= |X| = 2$ gilt $X = \{\hspace{0.05cm}{\rm A}, \hspace{0.15cm} {\rm B} \hspace{0.05cm}\}$ mit der Wahrscheinlichkeitsfunktion $($englisch: Probability Mass Function, $\rm PMF)$ $P_X(X)= \big (p_{\rm A},\hspace{0.15cm}p_{\rm B}\big)$ sowie den Quellensymbolwahrscheinlichkeiten $p_{\rm A}$ und $p_{\rm B}=1- p_{\rm A}$.
- Entsprechend gilt für eine Ternärquelle ⇒ $M_X= |X| = 3$: $X = \{\hspace{0.05cm}{\rm A}, \hspace{0.15cm} {\rm B}, \hspace{0.15cm} {\rm C} \hspace{0.05cm}\}$, $P_X(X)= \big (p_{\rm A},\hspace{0.15cm}p_{\rm B},\hspace{0.15cm}p_{\rm C}\big)$, $p_{\rm C}=1- p_{\rm A}-p_{\rm B}$.
Die Menge der möglichen Sinkensymbole wird durch die diskrete Zufallsgröße $Y$ charakterisiert. Diese entstammen der gleichen Symbolmenge wie die Quellensymbole ⇒ $M_Y=M_X = M$. Zur Vereinfachung der nachfolgenden Beschreibung bezeichnen wir diese mit Kleinbuchstaben, zum Beispiel für $M=3$: $Y = \{\hspace{0.05cm}{\rm a}, \hspace{0.15cm} {\rm b}, \hspace{0.15cm} {\rm c} \hspace{0.05cm}\}$.
Der Zusammenhang zwischen den Zufallsgrößen $X$ und $Y$ ist durch ein digitales Kanalmodell ohne Gedächtnis $($englisch: Discrete Memoryless Channel, $\rm DMC)$ festgelegt. Die linke Grafik zeigt dieses für $M=2$ und die rechte Grafik für $M=3$.
Die folgende Beschreibung gilt für den einfacheren Fall $M=2$. Für die Berechnung aller informationstheoretischer Größen im nächsten Abschnitt benötigen wir außer $P_X(X)$ und $P_Y(Y)$ noch die zweidimensionalen Wahrscheinlichkeitsfunktionen $($jeweils eine $2\times2$–Matrix$)$ aller
- bedingten Wahrscheinlichkeiten ⇒ $P_{\hspace{0.01cm}Y\hspace{0.03cm} \vert \hspace{0.01cm}X}(Y\hspace{0.03cm} \vert \hspace{0.03cm} X)$ ⇒ durch das DMC–Modell vorgegeben;
- Verbundwahrscheinlichkeiten ⇒ $P_{XY}(X,\hspace{0.1cm}Y)$;
- Rückschlusswahrscheinlichkeiten ⇒ $P_{\hspace{0.01cm}X\hspace{0.03cm} \vert \hspace{0.03cm}Y}(X\hspace{0.03cm} \vert \hspace{0.03cm} Y)$.
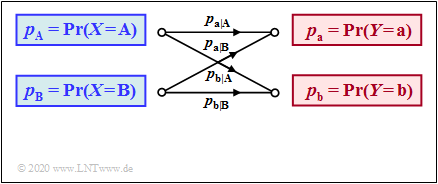
$\text{Beispiel 1}$: Wir betrachten den skizzierten Binärkanal.
- Die Verfälschungswahrscheinlichkeiten seien:
- $$\begin{align*}p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.95\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.05\hspace{0.05cm},\\ p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.40\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.60\end{align*}$$
- $$\Rightarrow \hspace{0.3cm} P_{\hspace{0.01cm}Y\hspace{0.05cm} \vert \hspace{0.05cm}X}(Y\hspace{0.05cm} \vert \hspace{0.05cm} X) = \begin{pmatrix} 0.95 & 0.05\\ 0.4 & 0.6 \end{pmatrix} \hspace{0.05cm}.$$
- Außerdem gehen wir von nicht gleichwahrscheinlichen Quellensymbolen aus:
- $$P_X(X) = \big ( p_{\rm A},\ p_{\rm B} \big )= \big ( 0.1,\ 0.9 \big ) \hspace{0.05cm}.$$
- Für die Wahrscheinlichkeitsfunktion der Sinke ergibt sich somit:
- $$P_Y(Y) = \big [ {\rm Pr}( Y\hspace{-0.1cm} = {\rm a})\hspace{0.05cm}, \ {\rm Pr}( Y \hspace{-0.1cm}= {\rm b}) \big ] = \big ( 0.1\hspace{0.05cm},\ 0.9 \big ) \cdot \begin{pmatrix} 0.95 & 0.05\\ 0.4 & 0.6 \end{pmatrix} $$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr}( Y \hspace{-0.1cm}= {\rm a}) = 0.1 \cdot 0.95 + 0.9 \cdot 0.4 = 0.455\hspace{0.05cm},\hspace{1.0cm} {\rm Pr}( Y \hspace{-0.1cm}= {\rm b}) = 1 - {\rm Pr}( Y \hspace{-0.1cm}= {\rm a}) = 0.545.$$
- Die Verbundwahrscheinlichkeiten $p_{\mu \kappa} = \text{Pr}\big[(X = μ) ∩ (Y = κ)\big]$ zwischen Quelle und Sinke sind:
- $$\begin{align*}p_{\rm Aa} & = p_{\rm a} \cdot p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} = 0.095\hspace{0.05cm},\hspace{0.5cm}p_{\rm Ab} = p_{\rm b} \cdot p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = 0.005\hspace{0.05cm},\\ p_{\rm Ba} & = p_{\rm a} \cdot p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} = 0.360\hspace{0.05cm}, \hspace{0.5cm}p_{\rm Bb} = p_{\rm b} \cdot p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = 0.540\hspace{0.05cm}. \end{align*}$$
- $$\Rightarrow \hspace{0.3cm} P_{XY}(X,\hspace{0.1cm}Y) = \begin{pmatrix} 0.095 & 0.005\\ 0.36 & 0.54 \end{pmatrix} \hspace{0.05cm}.$$
- Für die Rückschlusswahrscheinlichkeiten erhält man:
- $$\begin{align*}p_{\rm A\hspace{0.03cm}\vert \hspace{0.03cm}a} & = p_{\rm Aa}/p_{\rm a} = 0.095/0.455 = 0.2088\hspace{0.05cm},\hspace{0.5cm}p_{\rm A\hspace{0.03cm}\vert \hspace{0.03cm}b} = p_{\rm Ab}/p_{\rm b} = 0.005/0.545 = 0.0092\hspace{0.05cm},\\ p_{\rm B\hspace{0.03cm}\vert \hspace{0.03cm}a} & = p_{\rm Ba}/p_{\rm a} = 0.36/0.455 = 0.7912\hspace{0.05cm},\hspace{0.5cm}p_{\rm B\hspace{0.03cm}\vert \hspace{0.03cm}b} = p_{\rm Bb}/p_{\rm b} = 0.54/0.545 = 0.9908\hspace{0.05cm} \end{align*}$$
- $$\Rightarrow \hspace{0.3cm} P_{\hspace{0.01cm}X\hspace{0.05cm} \vert \hspace{0.05cm}Y}(X\hspace{0.05cm} \vert \hspace{0.05cm} Y) = \begin{pmatrix} 0.2088 & 0.0092\\ 0.7912 & 0.9908 \end{pmatrix} \hspace{0.05cm}.$$
Definition und Interpretation verschiedener Entropiefunktionen
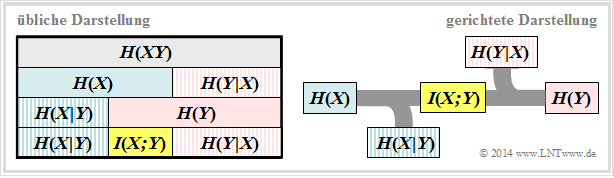
Im $\rm LNTwww$–Theorieteil werden alle für 2D–Zufallsgrößen relevanten Entropien definiert, die auch für die Digitalsignalübertragung gelten. Zudem finden Sie dort zwei Schaubilder, die den Zusammenhang zwischen den einzelnen Entropien illustrieren.
- Für die Digitalsignalübertragung ist die rechte Darstellung zweckmäßig, bei der die Richtung von der Quelle $X$ zur Sinke $Y$ erkennbar ist.
- Wir interpretieren nun ausgehend von dieser Grafik die einzelnen informationstheoretischen Größen.
- Die Quellenentropie (englisch: Source Entropy ) $H(X)$ bezeichnet den mittleren Informationsgehalt der Quellensymbolfolge. Mit dem Symbolumfang $|X|$ gilt:
- $$H(X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(X)}\right ] \hspace{0.1cm} = -{\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_X(X)}\big ] \hspace{0.2cm} =\hspace{0.2cm} \sum_{\mu = 1}^{|X|} P_X(x_{\mu}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(x_{\mu})} \hspace{0.05cm}.$$
- Die Äquivokation (auch Rückschlussentropie genannt, englisch: Equivocation ) $H(X|Y)$ gibt den mittleren Informationsgehalt an, den ein Betrachter, der über die Sinke $Y$ genau Bescheid weiß, durch Beobachtung der Quelle $X$ gewinnt:
- $$H(X|Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{-0.01cm}Y}(X\hspace{-0.01cm} |\hspace{0.03cm} Y)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{0.03cm}Y} (\hspace{0.05cm}x_{\mu}\hspace{0.03cm} |\hspace{0.05cm} y_{\kappa})} \hspace{0.05cm}.$$
- Die Äquivokation ist der Anteil der Quellenentropie $H(X)$, der durch Kanalstörungen (bei digitalem Kanal: Übertragungsfehler) verloren geht. Es verbleibt die Transinformation (englisch: Mutual Information) $I(X; Y)$, die zur Sinke gelangt:
- $$I(X;Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)}{P_X(X) \cdot P_Y(Y)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa})}{P_{\hspace{0.05cm}X}(\hspace{0.05cm}x_{\mu}) \cdot P_{\hspace{0.05cm}Y}(\hspace{0.05cm}y_{\kappa})} \hspace{0.05cm} = H(X) - H(X|Y) \hspace{0.05cm}.$$
- Die Irrelevanz (manchmal auch Streuentropie genannt, englisch: Irrelevance) $H(Y|X)$ gibt den mittleren Informationsgehalt an, den ein Betrachter, der über die Quelle $X$ genau Bescheid weiß, durch Beobachtung der Sinke $Y$ gewinnt:
- $$H(Y|X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{0.03cm} X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.03cm}X} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu})} \hspace{0.05cm}.$$
- Die Sinkenentropie $H(Y)$, der mittlere Informationsgehalt der Sinke, ist die Summe aus der nützlichen Transinformation $I(X; Y)$ und der Irrelevanz $H(Y|X)$, die ausschließlich von Kanalfehlern herrührt:
- $$H(Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_Y(Y)}\right ] \hspace{0.1cm} = -{\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_Y(Y)}\big ] \hspace{0.2cm} =I(X;Y) + H(Y|X) \hspace{0.05cm}.$$
- Die Verbundentropie $H(XY)$ gibt ist den mittleren Informationsgehalt der 2D–Zufallsgröße $XY$ an.  sie beschreibt zudem eine obere Schranke für die Summe aus Quellenentropie und Sinkenentropie:
- $$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] = \sum_{\mu = 1}^{|X|} \hspace{0.1cm} \sum_{\kappa = 1}^{|Y|} \hspace{0.1cm} P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa})}\le H(X) + H(Y) \hspace{0.05cm}.$$
$\text{Beispiel 2}$: Es gelten die gleichen Voraussetzungen wie für das $\text{Beispiel 1}$:
(1) Die Quellensymbole sind nicht gleichwahrscheinlich:
- $$P_X(X) = \big ( p_{\rm A},\ p_{\rm B} \big )= \big ( 0.1,\ 0.9 \big ) \hspace{0.05cm}.$$
(2) Die Verfälschungswahrscheinlichkeiten seien:
- $$\begin{align*}p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.95\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.05\hspace{0.05cm},\\ p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.40\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.60\end{align*}$$
- $$\Rightarrow \hspace{0.3cm} P_{\hspace{0.01cm}Y\hspace{0.05cm} \vert \hspace{0.05cm}X}(Y\hspace{0.05cm} \vert \hspace{0.05cm} X) = \begin{pmatrix} 0.95 & 0.05\\ 0.4 & 0.6 \end{pmatrix} \hspace{0.05cm}.$$
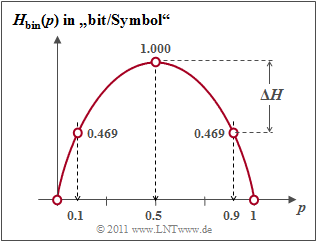
- Wegen Voraussetzung (1) erhält man so für die Quellenentropie mit der binären Entropiefunktion $H_{\rm bin}(p)$:
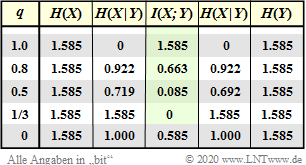
- $$H(X) = p_{\rm A} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm A}\hspace{0.1cm} } + p_{\rm B} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{p_{\rm B} }= H_{\rm bin} (p_{\rm A}) = H_{\rm bin} (0.1)= 0.469 \ {\rm bit} \hspace{0.05cm};$$
- $$H_{\rm bin} (p) = p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm} } + (1 - p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1 - p} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
- Entsprechend gilt für die Sinkenentropie mit der PMF $P_Y(Y) = \big ( p_{\rm a},\ p_{\rm b} \big )= \big ( 0.455,\ 0.545 \big )$:
- $$H(Y) = H_{\rm bin} (0.455)= 0.994 \ {\rm bit} \hspace{0.05cm}.$$
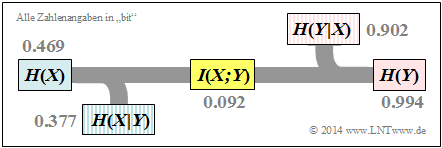
- Als nächstes berechnen wir die Verbundentropie:
- $$H(XY) = p_{\rm Aa} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Aa}\hspace{0.1cm} }+ p_{\rm Ab} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Ab}\hspace{0.1cm} }+p_{\rm Ba} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Ba}\hspace{0.1cm} }+ p_{\rm Bb} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Bb}\hspace{0.1cm} }$$
- $$\Rightarrow \hspace{0.3cm}H(XY) = 0.095 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.095 } +0.005 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.005 }+0.36 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.36 }+0.54 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.54 }= 1.371 \ {\rm bit} \hspace{0.05cm}.$$
Entsprechend dem oberen linken Schaubild sind somit auch die restlichen informationstheoretischen Größen berechenbar:
- die Äquivokation (oder Rückschlussentropie):
- $$H(X \vert Y) \hspace{-0.01cm} =\hspace{-0.01cm} H(XY) \hspace{-0.01cm} -\hspace{-0.01cm} H(Y) \hspace{-0.01cm} = \hspace{-0.01cm} 1.371\hspace{-0.01cm} -\hspace{-0.01cm} 0.994\hspace{-0.01cm} =\hspace{-0.01cm} 0.377\ {\rm bit} \hspace{0.05cm},$$
- die Irrelevanz (oder Streuentropie):
- $$H(Y \vert X) = H(XY) - H(X) = 1.371 - 0.994 = 0.902\ {\rm bit} \hspace{0.05cm}.$$
- die Transinformation (englisch Mutual Information):
- $$I(X;Y) = H(X) + H(Y) - H(XY) = 0.469 + 0.994 - 1.371 = 0.092\ {\rm bit} \hspace{0.05cm},$$
Die Ergebnisse sind in nebenstehender Grafik zusammengefasst.
Anmerkung: Äquivokation und Irrelevanz könnte man (allerdings mit Mehraufwand) auch direkt aus den entsprechenden Wahrscheinlichkeitsfunktionen berechnen, zum Beispiel:
- $$H(Y \vert X) = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.05cm}\in \hspace{0.05cm}XY} \hspace{-0.2cm} P_{XY}(x,\hspace{0.05cm}y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}\vert \hspace{0.03cm}X} (\hspace{0.05cm}y\hspace{0.03cm} \vert \hspace{0.05cm} x)}= p_{\rm Aa} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} } + p_{\rm Ab} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} } + p_{\rm Ba} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} } + p_{\rm Bb} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} } = 0.902 \ {\rm bit} \hspace{0.05cm}.$$
Rote Übergänge stehen für $p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} = p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = p_{\rm c\hspace{0.03cm}\vert \hspace{0.03cm}C} = q$ und blaue für $p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = p_{\rm c\hspace{0.03cm}\vert \hspace{0.03cm}A} =\text{...}= p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}C}= (1-q)/2$
$\text{Beispiel 3}$: Nun betrachten wir ein Übertragungssystem mit $M_X = M_Y = M=3$.
(1) Die Quellensymbole seien gleichwahrscheinlich:
- $$P_X(X) = \big ( p_{\rm A},\ p_{\rm B},\ p_{\rm C} \big )= \big ( 1/3,\ 1/3,\ 1/3 \big )\hspace{0.30cm}\Rightarrow\hspace{0.30cm}H(X)={\rm log_2}\hspace{0.1cm}3 \approx 1.585 \ {\rm bit} \hspace{0.05cm}.$$
(2) Das Kanalmodell ist symmetrisch ⇒ auch die Sinkensymbole sind gleichwahrscheinlich:
- $$P_Y(Y) = \big ( p_{\rm a},\ p_{\rm b},\ p_{\rm c} \big )= \big ( 1/3,\ 1/3,\ 1/3 \big )\hspace{0.30cm}\Rightarrow\hspace{0.30cm}H(Y)={\rm log_2}\hspace{0.1cm}3 \approx 1.585 \ {\rm bit} \hspace{0.05cm}.$$
(3) Die Verbundwahrscheinlichkeiten ergeben sich wie folgt:
- $$p_{\rm Aa}= p_{\rm Bb}= p_{\rm Cc}= q/M,$$
- $$p_{\rm Ab}= p_{\rm Ac}= p_{\rm Ba}= p_{\rm Bc} = p_{\rm Ca}= p_{\rm Cb} = (1-q)/(2M)$$
- $$\Rightarrow\hspace{0.30cm}H(XY) = 3 \cdot p_{\rm Aa} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Aa}\hspace{0.1cm} }+6 \cdot p_{\rm Ab} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Ab}\hspace{0.1cm} }= \ \text{...} \ = q \cdot {\rm log_2}\hspace{0.1cm}\frac{M}{q }+ (1-q) \cdot {\rm log_2}\hspace{0.1cm}\frac{M}{(1-q)/2 }.$$
(4) Für die Transinformation erhält man nach einigen Umformungen unter Berücksichtigung der Gleichung
- $$I(X;Y) = H(X) + H(Y) - H(XY)\text{:}$$
- $$\Rightarrow \hspace{0.3cm} I(X;Y) = {\rm log_2}\ (M) - (1-q) -H_{\rm bin}(q).$$
- Bei fehlerfreier Ternärübertragung $(q=1)$ gilt $I(X;Y) = H(X) = H(Y)={\rm log_2}\hspace{0.1cm}3$.
- Mit $q=0.8$ sinkt die Transinformaion schon auf $I(X;Y) = 0.663$ und mit $q=0.5$ auf $0.085$ bit.
- Der ungünstigste Fall aus informationstheoretischer Sicht ist $q=1/3$ ⇒ $I(X;Y) = 0$.
- Dagegen ist der aus der aus Sicht der Übertragungstheorie ungünstigste Fall $q=0$ ⇒ „kein einziges Übertragungssymbol kommt richtig an” aus informationstheoretischer Sicht gar nicht so schlecht.
- Um dieses gute Ergebnis nutzen zu können, ist allerdings sendeseitig eine Kanalcodierung erforderlich.
Definition und Bedeutung der Kanalkapazität
Berechnet man die Transinformation $I(X, Y)$ wie zuletzt im $\text{Beispiel 2}$ ausgeführt, so hängt diese nicht nur vom diskreten gedächtnislosen Kanal (englisch: Discrete Memoryless Channel, kurz DMC) ab, sondern auch von der Quellenstatistik ⇒ $P_X(X)$ ab. Ergo: Die Transinformation $I(X, Y)$ ist keine reine Kanalkenngröße.
$\text{Definition:}$ Die von Claude E. Shannon eingeführte Kanalkapazität (englisch: Channel Capacity) lautet gemäß seinem Standardwerk [Sha48][1]:
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
Oft wird die Zusatzeinheit „bit/Kanalzugriff” hinzugefügt, bei englischen Texten „bit/use”. Da nach dieser Definition stets die bestmögliche Quellenstatistik zugrunde liegt, hängt $C$ nur von den Kanaleigenschaften ⇒ $P_{Y \vert X}(Y \vert X)$ ab, nicht jedoch von der Quellenstatistik ⇒ $P_X(X)$.
Shannon benötigte die Kanalbeschreibungsgröße $C$ zur Formulierung des Kanalcodierungstheorems – eines der Highlights der von ihm begründeten Informationstheorie.
$\text{Shannons Kanalcodierungstheorem:}$
- Zu jedem Übertragungskanal mit der Kanalkapazität $C > 0$ existiert (mindestens) ein $(k,\ n)$–Blockcode, dessen (Block–)Fehlerwahrscheinlichkeit gegen Null geht, so lange die Coderate $R = k/n$ kleiner oder gleich der Kanalkapazität ist: $R ≤ C.$
- Voraussetzung hierfür ist allerdings, dass für die Blocklänge dieses Codes gilt: $n → ∞.$
$\text{Umkehrschluss von Shannons Kanalcodierungstheorem:}$
Ist die Rate $R$ des verwendeten $(n$, $k)$–Blockcodes größer als die Kanalkapazität $C$, so ist niemals eine beliebig kleine Blockfehlerwahrscheinlichkeit erreichbar.
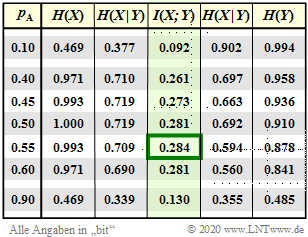
$\text{Beispiel 4}$: Wir betrachten den gleichen diskreten gedächtnislosen Kanal wie im $\text{Beispiel 2}$. In diesem $\text{Beispiel 2}$ wurden die Symbolwahrscheinlichkeiten $p_{\rm A} = 0.1$ und $p_{\rm B}= 1- p_{\rm A}=0.9$ vorausgesetzt. Damit ergab sich die Transinformation zu $I(X;Y)= 0.092$ bit/Kanalzugriff ⇒ siehe erste Zeile, vierte Spalte in der Tabelle.
Die Kanalkapazität ist die Transinformation $I(X, Y)$ bei bestmöglichen Symbolwahrscheinlichkeiten $p_{\rm A} = 0.55$ und $p_{\rm B}= 1- p_{\rm A}=0.45$:
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) = 0.284 \ \rm bit/Kanalzugriff \hspace{0.05cm}.$$
Aus der Tabelle erkennt man weiter (auf die Zusatzeinheit „bit/Kanalzugriff„ verzichten wir im Folgenden):
- Der Parameter $p_{\rm A} = 0.1$ war sehr ungünstig gewählt, weil beim vorliegenden Kanal das Symbol $\rm A$ mehr verfälscht wird als $\rm B$. Schon mit $p_{\rm A} = 0.9$ ergibt sich ein etwas besserer Wert: $I(X; Y)=0.130$.
- Aus dem gleichen Grund liefert $p_{\rm A} = 0.55$, $p_{\rm B} = 0.45$ ein etwas besseres Ergebnis als gleichwahrscheinliche Symbole $p_{\rm A} = p_{\rm B} =0.5$.
- Je unsymmetrischer der Kanal ist, um so mehr weicht die optimale Wahrscheinlichkeitsfunktion $P_X(X)$ von der Gleichverteilung ab. Im Umkehrschluss: Bei symmetrischem Kanal ergibt sich stets die Gleichverteilung.
Der Ternärkanal von $\text{Beispiel 3}$ ist symmetrisch. Deshalb ist hier $P_X(X) = \big ( 1/3,\ 1/3,\ 1/3 \big )$ für jeden $q$–Wert optimal, und die in der Ergebnistabelle angegebene Transinformation $I(X;Y)$ ist gleichzeitig die Kanalkapazität $C$.
Exercises
- First, select the number $(1,\ 2, \text{...} \ )$ of the task to be processed. The number "$0$" corresponds to a "Reset": Same setting as at program start.
- A task description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution".
- Source symbols are denoted by uppercase letters (binary: $\rm A$, $\rm B$), sink symbols by lowercase letters ($\rm a$, $\rm b$). Error-free transmission: $\rm A \rightarrow a$.
- For all entropy values, the unit "bit/use" would have to be added.
Deutsch:
- Wählen Sie zunächst die Nummer ($1$, $2$, ... ) der zu bearbeitenden Aufgabe. Die Nummer $0$ entspricht einem „Reset”: Einstellung wie beim Programmstart.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. Lösung nach Drücken von „Musterlösung”.
- Die Quellensymbole werden mit Großbuchstaben bezeichnet (binär: $\rm A$, $\rm B$), die Sinkenssymbole mit Kleinbuchstaben ($\rm a$, $\rm b$). Fehlerfreie Übertragung: $\rm A \rightarrow a$.
- Bei allen Entropiewerten müsste die Einheit „bit/use” hizugefügt werden.
(1) Let $p_{\rm A} = p_{\rm B} = 0.5$ and $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.1$. What is the channel model? What are the entropies $H(X), \, H(Y)$ and the mutual information $I(X;\, Y)$?
- Considered is the BSC model (Binary Symmetric Channel). Because of $p_{\rm A} = p_{\rm B} = 0.5$ holds for the entropies: $H(X) = H(Y) = 1$.
- Because of $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.1$ eqivocation and irrelevance are also equal: $H(X \vert Y) = H(Y \vert X) = H_{\rm bin}(p_{\rm b \vert A}) = H_{\rm bin}(0.1) =0.469$.
- The mutual information is $I(X;\, Y) = H(X) - H(X \vert Y)= 1-H_{\rm bin}(p_{\rm b \vert A}) = 0.531$ and the joint entropy is $H(XY) =1.469$.
(1) Es gelte $p_{\rm A} = p_{\rm B} = 0.5$ und $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.1$. Welches Kanalmodell liegt vor? Wie lauten die Entropien $H(X), \, H(Y)$ und die Transinformation $I(X;\, Y)$?
- Betrachtet wird das BSC–Modell (Binary Symmetric Channel). Wegen $p_{\rm A} = p_{\rm B} = 0.5$ gilt für die Quellen– und die Sinkenentropie: $H(X) = H(Y) = 1$.
- Wegen $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.1$ sind auch Äqivokation und Irrelevanz gleich: $H(X \vert Y) = H(Y \vert X) = H_{\rm bin}(p_{\rm b \vert A}) = H_{\rm bin}(0.1) =0.469$.
- Die Transinformation ist $I(X;\, Y) = H(X) - H(X \vert Y)= 1-H_{\rm bin}(p_{\rm b \vert A}) = 0.531$ und die Verbundentropie ist $H(XY) =1.469$.
(2) Let it continue $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.1$, but now the symbol probability $p_{\rm A} = 0. 9$. What is the capacity $C_{\rm BSC}$ of the BSC channel with $p_{\rm b \vert A} = p_{\rm a \vert B}$?
Which $p_{\rm b \vert A} = p_{\rm a \vert B}$ leads to the largest possible channel capacity and which $p_{\rm b \vert A} = p_{\rm a \vert B}$ leads to the channel capacity $C_{\rm BSC}=0$?
- The capacity $C_{\rm BSC}$ is equal to the maximum mutual information $I(X;\, Y)$ considering the optimal symbol probabilities.
- Due to the symmetry of the BSC model equally probable symbols $(p_{\rm A} = p_{\rm B} = 0.5)$ lead to the optimum ⇒ $C_{\rm BSC}=0.531$.
- The best is the "ideal channel" $(p_{\rm b \vert A} = p_{\rm a \vert B} = 0)$ ⇒ $C_{\rm BSC}=1$. The worst BSC channel results with $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.5$ ⇒ $C_{\rm BSC}=0$.
- But also with $p_{\rm b \vert A} = p_{\rm a \vert B} = 1$ we get $C_{\rm BSC}=1$. Here all symbols are inverted, which is information theoretically the same as $\langle Y_n \rangle \equiv \langle X_n \rangle$.
(2) Es gelte weiter $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.1$, aber nun ist die Symbolwahrscheinlichkeit $p_{\rm A} = 0.9$. Wie groß ist die Kapazität $C_{\rm BSC}$ des BSC–Kanals mit $p_{\rm b \vert A} = p_{\rm a \vert B}$?
- Welches $p_{\rm b \vert A} = p_{\rm a \vert B}$ führt zur größtmöglichen Kanalkapazität und welches $p_{\rm b \vert A} = p_{\rm a \vert B}$ zur Kanalkapazität $C_{\rm BSC}=0$?
- Die Kapazität $C_{\rm BSC}$ ist gleich der maximalen Transinformation $I(X;\, Y)$ unter Berücksichtigung der optimalen Symbolwahrscheinlichkeiten.
- Aufgrund der Symmetrie des BSC–Modells führen gleichwahrscheinliche Symbole $(p_{\rm A} = p_{\rm B} = 0.5)$ zum Optimum ⇒ $C_{\rm BSC}=0.531$.
- Am besten ist der ideale Kanal $(p_{\rm b \vert A} = p_{\rm a \vert B} = 0)$ ⇒ $C_{\rm BSC}=1$. Der schlechteste BSC–Kanal liegt durch $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.5$ fest ⇒ $C_{\rm BSC}=0$.
- Aber auch mit $p_{\rm b \vert A} = p_{\rm a \vert B} = 1$ ergibt sich $C_{\rm BSC}=1$. Hier werden alle Symbole invertiert, was informationstheoretisch das Gleiche ist wie $\langle Y_n \rangle \equiv \langle X_n \rangle$.
(3) Let $p_{\rm A} = p_{\rm B} = 0.5$, $p_{\rm b \vert A} = 0.05$ and $ p_{\rm a \vert B} = 0.4$. Interpret the results in comparison to the experiment $(1)$ and to the $\text{example 2}$ in the theory section.
- Unlike the experiment $(1)$ no BSC channel is present here. Rather, the channel considered here is asymmetric: $p_{\rm b \vert A} \ne p_{\rm a \vert B}$.
- According to $\text{Example 2}$ holds for $p_{\rm A} = 0.1,\ p_{\rm B} = 0.9$: $H(X)= 0.469$, $H(Y)= 0.994$, $H(X \vert Y)=0.377$, $H(Y \vert X)=0.902$, $I(X;\vert Y)=0.092$.
- Now holds $p_{\rm A} = p_{\rm B} = 0.5$ and we get $H(X)=1,000$, $H(Y)=0.910$, $H(X \vert Y)=0.719$, $H(Y \vert X)=0.629$, $I(X;\ Y)=0.281$.
- All output values depend significantly on $p_{\rm A}$ and $p_{\rm B}=1-p_{\rm A}$ except for the conditional probabilities ${\rm Pr}(Y \vert X)\in \{\hspace{0.05cm}0.95,\ 0.05,\ 0.4,\ 0.6\hspace{0.05cm} \}$.
(3) Es gelte $p_{\rm A} = p_{\rm B} = 0.5$, $p_{\rm b \vert A} = 0.05$ und $ p_{\rm a \vert B} = 0.4$. Interpretieren Sie die Ergebnisse im Vergleich zum Versuch (1) sowie zum $\text{Beispiel 2}$ im Theorieteil.
- Im Gegensatz zum Versuch (1) liegt hier kein BSC-Kanal vor. Vielmehr ist der hier betrachtete Kanal unsymmetrisch: $p_{\rm b \vert A} \ne p_{\rm a \vert B}$.
- Gemäß $\text{Beispiel 2}$ gilt für $p_{\rm A} = 0.1,\ p_{\rm B} = 0.9$: $H(X)= 0.469$, $H(Y)= 0.994$, $H(X \vert Y)=0.377$, $H(Y \vert X)=0.902$, $I(X;\ Y)=0.092$.
- Nun gilt $p_{\rm A} = p_{\rm B} = 0.5$ und man erhält $H(X)= 1.000$, $H(Y)= 0.910$, $H(X \vert Y)=0.719$, $H(Y \vert X)=0.629$, $I(X;\ Y)=0.281$.
- Alle Ausgabewerte hängen signifikant von $p_{\rm A}$ und $p_{\rm B}=1-p_{\rm A}$ ab mit Ausnahme der bedingten Wahrscheinlichkeiten ${\rm Pr}(Y \vert X)\ \in \ \{\hspace{0.05cm}0.95,\ 0.05,\ 0.4,\ 0.6\hspace{0.05cm} \}$.
(4) Let it continue $p_{\rm A} = p_{\rm B}$, $p_{\rm b \vert A} = 0.05$, $ p_{\rm a \vert B} = 0.4$. What differences do you see in terms of analytical calculation and „simulation” $(N=10000)$.
- The joint probabilities are $p_{\rm Aa} =0.475$, $p_{\rm Ab} =0.025$, $p_{\rm Ba} =0.200$, $p_{\rm Bb} =0.300$. Simulation: Approximation by relative frequencies:
- For example, for $N=10000$: $h_{\rm Aa} =0.4778$, $h_{\rm Ab} =0.0264$, $h_{\rm Ba} =0.2039$, $h_{\rm Bb} =0.2919$. After pressing "New sequence" slightly different values.
- For all subsequent calculations, no principal difference between theory and simulation, except $p \to h$. Examples:
- $p_{\rm A} = 0.5 \to h_{\rm A}=h_{\rm Aa} + h_{\rm Ab} =0.5042$, $p_b = 0.325 \to h_{\rm b}=h_{\rm Ab} + h_{\rm Bb} =0. 318$, $p_{b|A} = 0.05 \to h_{\rm b|A}=h_{\rm Ab}/h_{\rm A} =0.0264/0.5042= 0.0524$,
- $p_{\rm A|b} = 0.0769 \to h_{\rm A|b}=h_{\rm Ab}/h_{\rm b} =0.0264/0.318= 0.0830$. Thus, this simulation yields $I_{\rm Sim}(X;\ Y)=0.269$ instead of $I(X;\ Y)=0.281$.
Dum
(4) Es gelte weiter $p_{\rm A} = p_{\rm B}$, $p_{\rm b \vert A} = 0.05$, $ p_{\rm a \vert B} = 0.4$. Welche Unterschiede erkennen Sie hinsichtlich analytischer Berechnung und „Simulation” $(N=10000)$.
- Die Verbundwahrscheinlichkeiten sind $p_{\rm Aa} =0.475$, $p_{\rm Ab} =0.025$, $p_{\rm Ba} =0.200$, $p_{\rm Bb} =0.300$. Simulation: Approximation durch relative Häufigkeiten:
- Zum Beispiel für $N=10000$: $h_{\rm Aa} =0.4778$, $h_{\rm Ab} =0.0264$, $h_{\rm Ba} =0.2039$, $h_{\rm Bb} =0.2919$. Nach Drücken „Neue Folge” etwas andere Werte.
- Für alle nachfolgenden Berechnungen kein prinzieller Unterschied zwischen Theorie und Simulation, außer $p \to h$. Beispiele:
- $p_{\rm A} = 0.5 \to h_{\rm A}=h_{\rm Aa} + h_{\rm Ab} =0.5042$, $p_b = 0.325 \to h_{\rm b}=h_{\rm Ab} + h_{\rm Bb} =0.318$, $p_{b|A} = 0.05 \to h_{\rm b|A}=h_{\rm Ab}/h_{\rm A} =0.0264/0.5042= 0.0524$,
- $p_{\rm A|b} = 0.0769 \to h_{\rm A|b}=h_{\rm Ab}/h_{\rm b} =0.0264/0.318= 0.0830$. Dadurch liefert diese Simulation $I_{\rm Sim}(X;\ Y)=0.269$ anstelle von $I(X;\ Y)=0.281$.
(5) Setting according to $(4)$. How does $I_{\rm Sim}(X;\ Y)$ differ from $I(X;\ Y) = 0.281$ for $N=10^3$, $10^4$, $10^5$ ? In each case, averaging over ten realizations.
- $N=10^3$: $0.232 \le I_{\rm Sim} \le 0.295$, mean: $0.263$ # $N=10^4$: $0.267 \le I_{\rm Sim} \le 0.293$, mean: $0.279$ # $N=10^5$: $0.280 \le I_{\rm Sim} \le 0.285$ mean: $0.282$.
- With $N=10^6$ for this channel, the simulation result differs from the theoretical value by less than $\pm 0.001$.
(5) Einstellung gemäß $(4)$. Wie unterscheidet sich $I_{\rm Sim}(X;\ Y)$ für $N=10^3$, $10^4$, $10^5$ von $I(X;\ Y) = 0.281$ ? Jeweils Mittelung über zehn Realisierungen.
- $N=10^3$: $0.232 \le I_{\rm Sim} \le 0.295$, Mittelwert: $0.263$ # $N=10^4$: $0.267 \le I_{\rm Sim} \le 0.293$ MW: $0.279$ # $N=10^5$: $0.280 \le I_{\rm Sim} \le 0.285$ MW: $0.282$.
- Mit $N=10^6$ unterscheidet sich bei diesem Kanal das Simulationsergebnis vom theoretischen Wert um weniger als $\pm 0.001$.
(6) What is the capacity $C_6$ of this channel with $p_{\rm b \vert A} = 0.05$, $ p_{\rm a \vert B} = 0.4$? Is the error probability $0$ possible with the code rate $R=0.3$?
- $C_6=0.284$ is the maximum of $I(X;\ Y)$ for $p_{\rm A} =0.55$ ⇒ $p_{\rm B} =0. 45$. Simulation over ten times $N=10^5$: $0.281 \le I_{\rm Sim}(X;\ Y) \le 0.289$.
- With the code rate $R=0.3 > C_6$ an arbitrarily small block error probability is not achievable even with the best possible coding.
(6) Wie groß ist die Kapazität $C_6$ dieses Kanals mit $p_{\rm b \vert A} = 0.05$, $ p_{\rm a \vert B} = 0.4$? Ist mit der Coderate $R=0.3$ die Fehlerwahrscheinlichkeit $0$ möglich?
- $C_6=0.284$ ist das Maximum von $I(X;\ Y)$ für $p_{\rm A} =0.55$ ⇒ $p_{\rm B} =0.45$. Simulation über zehnmal $N=10^5$: $0.281 \le I_{\rm Sim}(X;\ Y) \le 0.289$.
- Mit der Coderate $R=0.3 > C_6$ ist auch bei bestmöglicher Codierung eine beliebig kleine Blockfehlerwahrscheinlichkeit nicht erreichbar.
(7) Now let $p_{\rm A} = p_{\rm B}$, $p_{\rm b \vert A} = 0.5$, $ p_{\rm a \vert B} = 0$. What property does this asymmetric channel exhibit? What values result for $H(X)$, $H(X \vert Y)$, $I(X;\ Y)$ ?
- The symbol $\rm A$ is never falsified, the symbol $\rm B$ with (information theoretically) maximum falsification probability $ p_{\rm a \vert B} = 0.5$
- The total falsification probability is $ {\rm Pr} (Y_n \ne X_n)= p_{\rm A} \cdot p_{\rm b \vert A} + p_{\rm B} \cdot p_{\rm a \vert B}= 0.25$ ⇒ about $25\%$ of the output sink symbols are "purple".
- Joint probabilities: $p_{\rm Aa}= 1/2,\ p_{\rm Ab}= 0,\ p_{\rm Ba}= p_{\rm Bb}= 1/4$, Inference probabilities: $p_{\rm A \vert a}= 1,\ p_{\rm B \vert a}= 0,\ p_{\rm A \vert b}= 1/3,\ p_{\rm B \vert b}= 2/3$.
- From this we get for equivocation $H(X \vert Y)=0.689$; with source entropy $H(X)= 1$ ⇒ $I(X;\vert Y)=H(X)-H(X \vert Y)=0.311$.
(7) Nun gelte $p_{\rm A} = p_{\rm B}$, $p_{\rm b \vert A} = 0.5$, $ p_{\rm a \vert B} = 0$. Welche Eigenschaft zeigt dieser unsymmetrische Kanal? Welche Werte ergeben sich für $H(X)$, $H(X \vert Y)$, $I(X;\ Y)$ ?
- Das Symbol $\rm A$ wird niemals verfälscht, das Symbol $\rm B$ mit (informationstheoretisch) maximaler Verfälschungswahrscheinlichkeit $ p_{\rm a \vert B} = 0.5$
- Die gesamte Verfälschungswahrscheinlichkeit ist $ {\rm Pr} (Y_n \ne X_n)= p_{\rm A} \cdot p_{\rm b \vert A} + p_{\rm B} \cdot p_{\rm a \vert B}= 0.25$ ⇒ ca. $25\%$ der ausgegebenen Sinkensymbole sind violett.
- Verbundwahrscheinlichkeiten: $p_{\rm Aa}= 1/2,\ p_{\rm Ab}= 0,\ p_{\rm Ba}= p_{\rm Bb}= 1/4$, Rückschlusswahrscheinlichkeiten: $p_{\rm A \vert a}= 1,\ p_{\rm B \vert a}= 0,\ p_{\rm A \vert b}= 1/3,\ p_{\rm B \vert b}= 2/3$.
- Daraus erhält man für die Äquivokation $H(X \vert Y)=0.689$; mit Quellenentropie $H(X)= 1$ ⇒ $I(X;\ Y)=H(X)-H(X \vert Y)=0.311$.
(8) What is the capacity $C_8$ of this channel with $p_{\rm b \vert A} = 0.5$, $ p_{\rm a \vert B} = 0.4$? Is the error probability $0$ possible with the code rate $R=0.3$?
- $C_8=0.322$ is the maximum of $I(X;\ Y)$ for $p_{\rm A} =0.4$. Thus, because of $C_8 >R=0.3 $ an arbitrarily small block error probability is achievable.
- $H(X)=0.971$ is smaller than in $(7)$ by $0.29$ and $H(X \vert Y)=0.649$ smaller by $0.4$ ⇒ larger channel capacity: $C_8=0.971-0.649=0.322 > C_6$.
- Joint probabilities: $p_{\rm Aa}= p_{\rm Ab}= 1/5,\ p_{\rm Ba}= 0,\ p_{\rm Bb}= 3/5$. Inference probabilities: $p_{\rm A \vert a}= 1,\ p_{\rm B \vert a}= 0,\ p_{\rm A \vert b}= 1/4,\ p_{\rm B \vert b}= 3/4$.
- Insignificantly, there are now also fewer violet sink symbols in the uncoded case $(20\%$ instead of $25\%$; with $p_{\rm A} =0$ there would be none$)$.
- The only decisive factor is the channel capacity $C_8=0.322$ ⇒ there is a code with rate $R \le0.322$ with arbitrarily small block error probability.
(8) Wie groß ist die Kapazität $C_8$ dieses Kanals mit $p_{\rm b \vert A} = 0.5$, $ p_{\rm a \vert B} = 0.4$? Ist mit der Coderate $R=0.3$ die Fehlerwahrscheinlichkeit $0$ möglich?
- $C_8=0.322$ ist das Maximum von $I(X;\ Y)$ für $p_{\rm A} =0.4$. Wegen $C_8 >R=0.3 $ ist somit eine beliebig kleine Blockfehlerwahrscheinlichkeit erreichbar.
- $H(X)= 0.971$ ist um $0.29$ kleiner, $H(X \vert Y)=0.649$ um $0.4$ kleiner als in (7) ⇒ größere Kanalkapazität: $C_8=0.971-0.649=0.322 > C_6$.
- Verbundwahrscheinlichkeiten: $p_{\rm Aa}= p_{\rm Ab}= 1/5,\ p_{\rm Ba}= 0,\ p_{\rm Bb}= 3/5$, Rückschlusswahrscheinlichkeiten: $p_{\rm A \vert a}= 1,\ p_{\rm B \vert a}= 0,\ p_{\rm A \vert b}= 1/4,\ p_{\rm B \vert b}= 3/4$.
- Unwesentlich ist, dass es nun auch im uncodierten Fall weniger violette Sinkensymbole gibt $(20\%$ statt $25\%$; mit $p_{\rm A} =0$ gäbe es gar keine$)$.
- Entscheidend ist allein die Kanalkapazität $C_8=0.322$ ⇒ es gibt einen Code mit Rate $R \le0.322$ mit beliebig kleiner Blockfehlerwahrscheinlichkeit.
(9) We consider the ideal ternary channel: $p_{\rm a \vert A} = p_{\rm b \vert B}=p_{\rm c \vert C}=1$. What is its capacity $C_9$? What is the maximum mutual information displayed by the program?
- Due to the symmetry of the channel model, equally probable symbols $(p_{\rm A} = p_{\rm B}=p_{\rm C}=1/3)$ lead to the channel capacity: $C_9 = \log_2\ (3) = 1.585$.
- Since in the program all parameter values can only be entered with a resolution of $0.05$ , for $I(X;\ Y)$ this maximum value is not reached.
- Possible approximations: $p_{\rm A} = p_{\rm B}= 0.3, \ p_{\rm C}=0.4$ ⇒ $I(X;\ Y)= 1. 571$ # $p_{\rm A} = p_{\rm B}= 0.35, \ p_{\rm C}=0.3$ ⇒ $I(X;\ Y)= 1.581$.
(9) Wir betrachten den idealen Ternärkanal: $p_{\rm a \vert A} = p_{\rm b \vert B}=p_{\rm c \vert C}=1$. Wie groß ist dessen Kapazität $C_9$? Welche maximale Transinformation zeigt das Programm an?
- Aufgrund der Symmetrie des Kanalmodells führen gleichwahrscheinliche Symbole $(p_{\rm A} = p_{\rm B}=p_{\rm C}=1/3)$ zur Kanalkapazität: $C_9 = \log_2\ (3) = 1.585$.
- Da im Programm alle Parameterwerte nur mit einer Auflösung von $0.05$ eingebbar sind, wird für $I(X;\ Y)$ dieser Maximalwert nicht erreicht.
- Mögliche Approximationen: $p_{\rm A} = p_{\rm B}= 0.3, \ p_{\rm C}=0.4$ ⇒ $I(X;\ Y)= 1.571$ # $p_{\rm A} = p_{\rm B}= 0.35, \ p_{\rm C}=0.3$ ⇒ $I(X;\ Y)= 1.581$.
(10) Let the source symbols be (nearly) equally probable. Interpret the other settings and the results.
- The falsification probabilities are $p_{\rm b \vert A} = p_{\rm c \vert B}=p_{\rm a \vert C}=1$ ⇒ no single sink symbol is equal to the source symbol.
- This cyclic mapping has no effect on the channel capacity: $C_{10} = C_9 = 1.585$. The program returns ${\rm Max}\big[I(X;\ Y)\big]= 1.581$.
(10) Die Quellensymbole seien („quasi”)–gleichwahrscheinlich. Interpretieren Sie die weiteren Einstellungen und die Ergebnisse.
- Die Verfälschungswahrscheinlichkeiten sind $p_{\rm b \vert A} = p_{\rm c \vert B}=p_{\rm a \vert C}=1$ ⇒ kein einziges Sinkensymbol ist gleich dem Quellensymbol.
- Dieses zyklische Mapping hat keinen Einfluss auf die Kanalkapazität: $C_{10} = C_9 = 1.585$. Das Programm liefert wieder ${\rm Max}\big[I(X;\ Y)\big]= 1.581$.
(11) We consider up to and including $(13)$ the same ternary source. What results are obtained for $p_{\rm b \vert A} = p_{\rm c \vert B}=p_{\rm a \vert C}=0.2$ and $p_{\rm c \vert A} = p_{\rm a \vert B}=p_{\rm b \vert C}=0$?
- Each symbol can only be corrupted into one of the two possible other symbols. From $p_{\rm b \vert A} = p_{\rm c \vert B}=p_{\rm a \vert C}=0.2$ it follows $p_{\rm a \vert A} = p_{\rm b \vert B}=p_{\rm c \vert C}=0.8$.
- This gives us for the maximum mutual information ${\rm Max}\big[I(X;\ Y)\big]= 0.861$ and for the channel capacity a slightly larger value: $C_{11} \gnapprox 0.861$.
(11) Wir betrachten bis einschließlich (13) die gleiche Ternärquelle. Welche Ergebnisse erhält man für $p_{\rm b \vert A} = p_{\rm c \vert B}=p_{\rm a \vert C}=0.2$ und $p_{\rm c \vert A} = p_{\rm a \vert B}=p_{\rm b \vert C}=0$?
- Jedes Symbol kann nur in eines der zwei möglichen anderen Symbole verfälscht werden. Aus $p_{\rm b \vert A} = p_{\rm c \vert B}=p_{\rm a \vert C}=0.2$ folgt $p_{\rm a \vert A} = p_{\rm b \vert B}=p_{\rm c \vert C}=0.8$.
- Damit erhält man für die maximale Transinformation ${\rm Max}\big[I(X;\ Y)\big]= 0.861$ und für die Kanalkapazität einen geringfügig größeren Wert: $C_{11} \gnapprox 0.861$.
(12) How do the results change if each symbol is transferred to $80\%$ correct and corrupted to each $10\%$ in one of the other two symbols?
- Although the probability of correct transmission is $80\%$ as large as in (11), here the channel capacity is smaller by about $0.2$.
- If one knows with the channel $(11)$ that $X = \rm A$ has been falsified, one also knows $Y = \rm b$. But not with channel $(12)$ ⇒ the channel is less favorable.
Dummy
(12) Wie ändern sich die Ergebnisse, wenn jedes Symbol zu $80\%$ richtig übertragen und zu je $10\%$ in eines der beiden anderen Symbole verfälscht wird?
- Obwohl die Wahrscheinlichkeit für eine richtige Übertragung mit $80\%$ ebenso groß ist wie in (11), ist hier die Kanalkapazität um etwa den Wert $0.2$ kleiner.
- Weiß man beim Kanal (11), dass $X = \rm A$ verfälscht wurde, so weiß man auch, dass $Y = \rm b$ ist. Bei (12) weiß man das nicht ⇒ der Kanal ist ungünstiger.
(13) Let the falsification probabilities now $p_{\rm b \vert A} = p_{\rm c \vert A} = p_{\rm a \vert B} = p_{\rm c \vert B}=p_{\rm a \vert C}=p_{\rm b \vert C}=0.5$. Interpret this redundancy-free ternary channel.
- No single sink symbol is equal to its associated source symbol; with respect to the other two symbols, a $50\hspace{-0.1cm}:\hspace{-0.1cm}50$ decision must be made.
- Nevertheless, here the channel capacity is $C_{13} \gnapprox 0.584$ only slightly smaller than in the previous experiment: $C_{12} \gnapprox 0.661$.
- The channel capacity $C=0$ results for the redundancy-free ternary channel exactly for the case where all nine falsification probabilities are equal $1/3$ .
(13) Die Verfälschungswahrscheinlichkeiten seien nun $p_{\rm b \vert A} = p_{\rm c \vert A} = p_{\rm a \vert B} = p_{\rm c \vert B}=p_{\rm a \vert C}=p_{\rm b \vert C}=0.5$. Interpretieren Sie diesen redundanzfreien Ternärkanal.
- Kein einziges Sinkensymbol ist gleich dem zugehörigen Quellensymbol; bezüglich der beiden anderen Symbole ist eine $50\hspace{-0.1cm}:\hspace{-0.1cm}50$–Entscheidung zu treffen.
- Trotzdem ist hier die Kanalkapazität mit $C_{13} \gnapprox 0.584$ nur geringfügig kleiner als im vorherigen Versuch: $C_{12} \gnapprox 0.661$.
- Die Kanalapazität $C=0$ ergibt sich beim redundanzfreien Ternärkanal genau für den Fall, dass alle neun Verfälschungswahrscheinlichkeiten gleich $1/3$ sind.
(14) What is the capacity $C_{14}$ of the ternary channel with $p_{\rm b \vert A} = p_{\rm a \vert B}= 0$ and $p_{\rm c \vert A} = p_{\rm c \vert B} = p_{\rm a \vert C}=p_{\rm b \vert C}=0. 1$ ⇒ $p_{\rm a \vert A} = p_{\rm b \vert B}=0.9$, $p_{\rm c \vert C} =0.8$?
- With the default $p_{\rm A}=p_{\rm B}=0.2$ ⇒ $p_{\rm C}=0.6$ we get $I(X;\ Y)= 0.738$. What we are looking for now are „better” symbol probabilities.
- From the symmetry of the channel, it is obvious that $p_{\rm A}=p_{\rm B}$ is optimal. The channel capacity $C_{14}=0.995$ is obtained for $p_{\rm A}=p_{\rm B}=0.4$ ⇒ $p_{\rm C}=0.2$.
- Example: Ternary transfer if the middle symbol $\rm C$ can be distorted in two directions, but the outer symbols can only be distorted in one direction at a time.
(14) Welche Kapazität $C_{14}$ besitzt der Ternärkanal mit $p_{\rm b \vert A} = p_{\rm a \vert B}= 0$ und $p_{\rm c \vert A} = p_{\rm c \vert B} = p_{\rm a \vert C}=p_{\rm b \vert C}=0.1$ ⇒ $p_{\rm a \vert A} = p_{\rm b \vert B}=0.9$, $p_{\rm c \vert C} =0.8$?
- Mit der Voreinstellung $p_{\rm A}=p_{\rm B}=0.2$ ⇒ $p_{\rm C}=0.6$ ergibt sich $I(X;\ Y)= 0.738$. Gesucht sind nun „bessere” Symbolwahrscheinlichkeiten.
- Aus der Symmetrie des Kanals ist offensichtlich, dass $p_{\rm A}=p_{\rm B}$ optimal ist. Die Kanalkapazität $C_{14}=0.995$ ergibt sich für $p_{\rm A}=p_{\rm B}=0.4$ ⇒ $p_{\rm C}=0.2$.
- Beispiel: Ternärübertragung, falls das mittlere Symbol $\rm C$ in zwei Richtungen verfälscht werden kann, die äußeren Symbole aber jeweils nur in eine Richtung.
Applet Manual
(A) Auswahlmöglichkeit, ob „analytisch” oder „per Simulation”
(B) Einstellung des Parameters $N$ für die Simulation
(C) Auswahlmöglichkeit, ob „Binärquelle” oder „Ternärquelle”
(D) Einstellung der Symbolwahrscheinlichkeiten
(E) Einstellung der Übergangswahrscheinlichkeiten
(F) Numerikausgabe verschiedener Wahrscheinlichkeiten
(G) Zwei Schaubilder mit den informationstheoretischen Größen
(H) Ausgabe einer beispielhaften Quellensymbolfolge
(I) Zugehörige simulierte Sinkensymbolfolge
(J) Bereich für Übungen: Aufgabenauswahl, Fragen, Musterlösungen
About the Authors
This interactive calculation tool was designed and implemented at the Institute for Communications Engineering at the Technical University of Munich.
- The first version was created in 2010 by Martin Völkl as part of his diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder and Klaus Eichin).
- In 2020 the program was redesigned via HTML5/JavaScript by Veronika Hofmann (Ingenieurspraxis Mathematik, Supervisor: Benedikt Leible and Tasnád Kernetzky ).
- Last revision and English version 2021 by Carolin Mirschina in the context of a working student activity. Translation using DEEPL.com (free version).
- The conversion of this applet was financially supported by "Studienzuschüsse" (TUM Department of Electrical and Computer Engineering). We thank.
Once again: Open Applet in new Tab
- ↑ Shannon, C.E.: A Mathematical Theory of Communication. In: Bell Syst. Techn. J. 27 (1948), S. 379-423 und S. 623-656.