Aufgaben:Exercise 1.1: Music Signals

• Return to book

Music signals, original,
noisy and/or distorted?

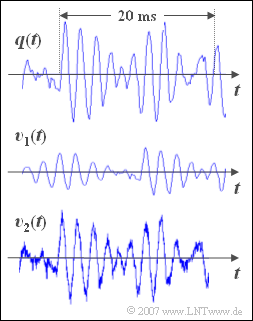
On the right you see a  $\text{30 ms}$  long section of a music signal  \(q(t)\).  It is the piece  "For Elise"  by Ludwig van Beethoven.

• Underneath are drawn two sink signals  \(v_1(t)\)  and  \(v_2(t)\), which were recorded after the transmission of the music signal  \(q(t)\)  over two different channels.

• The following operating elements allow you to listen to the first fourteen seconds of each of the three audio signals  \(q(t)\),  \(v_1(t)\)  and  \(v_2(t)\).

Original signal  \(q(t)\):

Sink signal  \(v_1(t)\):

Sink signal  \(v_2(t)\):

Notes:

• The task belongs to the chapter Principles of Communication.

Questions

1

Estimate the signal frequency of  \(q(t)\)  in the displayed section.

	The signal frequency is approximately  \(f = 250\,\text{Hz}\).
	The signal frequency is approximately  \(f = 500\,\text{Hz}\).
	The signal frequency is about  \(f = 1\,\text{kHz}\).

2

Which statements are true for the signal  \(v_1(t)\) ?

	The signal  \(v_1(t)\)  is undistorted compared to  \(q(t)\).
	The signal  \(v_1(t)\)  shows distortions compared to  \(q(t)\) .
	The signal  \(v_1(t)\)  is noisy compared to  \(q(t)\) .

3

Which statements are true for the signal  \(v_2(t)\) ?

	The signal  \(v_2(t)\)  is undistorted compared to  \(q(t)\) .
	The signal  \(v_2(t)\)  shows distortions compared to  \(q(t)\) .
	The signal  \(v_2(t)\)  is noisy compared to  \(q(t)\) .

4

One of the signals is undistorted and not noisy compared to the original   \(q(t)\) .
Estimate the attenuation factor and the running time for this.

\( \alpha \ = \ \)

\( \tau \ = \ \) $\ \text{ms}$

Solution

Solution

(1)  Correct is the solution 2:

• In the marked range of $20$ milliseconds approx.   $10$  oscillations can be detected.
• From this the result  follows approximately for the signal frequency; $f = {10}/(20 \,\text{ms}) = 500 \,\text{Hz}$.

(2)  Correct is the solution 1:

• The signal  \(v_1(t)\)  is undistorted compared to the original signal \(q(t)\). The following applies:   $v_1(t)=\alpha \cdot q(t-\tau) .$

• An attenuation  \(\alpha\)  and a delay  \(\tau\)  do not cause distortion, but the signal is then only quieter and delayed in time, compared to the original.

(3)  Correct are the solutions 1 and 3:

• One can recognize both in the displayed signal  \(v_2(t)\)  and in the audio signal  additive noise   ⇒   solution 3.
• The signal-to-noise ratio is approx.   $\text{30 dB}$; but this cannot be seen from this representation.
• Correct is also the solution 1:   Without this noise component  \(v_2(t)\)  identical with  \(q(t)\).

(4)  The signal  \(v_1(t)\)  is identical in form to the original signal  \(q(t)\)  and differs from it only

• by the attenuation factor  $\alpha = \underline{\text{0.3}}$  (dies entspricht etwa  $\text{–10 dB)}$
• and the delay  $\tau = \underline{10\,\text{ms}}$.