Aufgaben:Exercise 5.5Z: Complexity of the FFT

• Return to book

Final step of the FFT for $N=8$

The  $\rm FFT$  algorithm  ("Fast Fourier Transform")  realises a  "Discrete Fourier Transform"  $\rm (DFT)$  with the smallest possible computational effort if the parameter  $N$  is a power of two.  In detail, the following calculation steps are necessary to carry out an FFT:

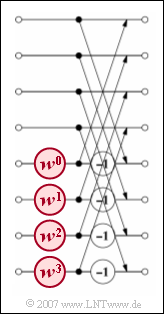
• The FFT occurs in  ${\rm log_2} \ N$  stages, whereby the exact same number of arithmetic operations must be carried out in each stage.
• The diagram shows the third and last stage for the example  $N = 8$.  It can be seen that  $N/2$  basic operations have to be carried out in this and the other stages.
• In each basic operation called   butterfly,  two complex outputs are calculated from the two complex input variables  $E_1$  and  $E_2$ :

$$A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu},$$

$$A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$

• Here  $w = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi/N}$  denotes the complex rotation factor.  For  $N = 8$  the value  $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/4} = \cos(45^\circ) - {\rm j} \cdot \sin(45^\circ)\hspace{0.05cm}$ is obtained.
• The exponent  $\mu$  for this complex rotation factor can take all integer values between  $0$  and  $N/2-1$.  For  $N = 8$  it is:

$$w^0 = 1,\hspace{0.2cm}w^1 = {1}/{\sqrt{2}}- {\rm j} \cdot{1}/{\sqrt{2}},\hspace{0.2cm}w^2 = - {\rm j},\hspace{0.2cm}w^3 = -{1}/{\sqrt{2}}- {\rm j} \cdot{1}/{\sqrt{2}} \hspace{0.05cm}.$$

The purpose of this task is to determine the number of arithmetic operations  $(\mathcal{O}_{\rm FFT})$  required for the FFT and compare it with the value  $\mathcal{O}_{\rm DFT} ≈ 8\cdot N^2$  that can be specified for the DFT.

Hints:

• This task belongs to the chapter  Fast Fourier Transform (FFT).
• It makes sense to calculate the powers of  $w$  before the actual algorithm and store them in a lookup table.  The operations necessary for this are to be disregarded.
• The  "bit reversal operation"  – a rearrangement that has to be carried out before the first stage – is also not to be taken into account in this estimation.

Questions

1

How many real additions  $(A_{\rm A})$  does a complex addition require?

$A_{\rm A} \hspace{0.3cm} = \ $

2

How many real additions  $(A_{\rm M})$  and multiplications  $(M_{\rm M})$  are required for a complex multiplication?

$A_{\rm M} \hspace{0.3cm} = \ $

$M_{\rm M} \hspace{0.2cm} = \ $

3

How many complex additions/subtractions  $(a_{\rm B})$  does a single basic operationn  ("butterfly")  require?
How many complex multiplications  $(m_{\rm B})$  are required per basic operation?

$a_{\rm B} \hspace{0.32cm} = \ $

$m_{\rm B} \hspace{0.2cm} = \ $

4

How many arithmetic operations  (additions, subtractions, multiplications alike)  does a basic operation require?

$\mathcal{O}_{\rm B} \ = \ $

5

How many real operations  $(\mathcal{O}_{\rm FFT})$  does the entire FFT–algorithm require?  What are the values for  $N = 16$  und  $N = 1024$?

$N = 16\text{:} \hspace{0.65cm} \mathcal{O}_{\rm FFT} \ = \ $

$N = 1024\text{:} \hspace{0.2cm} \mathcal{O}_{\rm FFT} \ = \ $

6

What is the time gain  $G_{\rm FFT} = \mathcal{O}_{\rm DFT} - \mathcal{O}_{\rm FFT}$  for  $N = 16$  and  $N = 1024$?

$N = 16\text{:} \hspace{0.65cm} G_{\rm FFT} \ = \ $

$N = 1024\text{:} \hspace{0.2cm} G_{\rm FFT} \ = \ $

Solution

Solution

(1)  Each complex addition requires two real additions:

$$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + R_2) + {\rm j} \cdot (I_1 + I_2)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.15 cm}\underline{ A_{\rm A} = 2}\hspace{0.05cm}.$$

(2)  Any complex multiplication requires four real multiplications and two real additions:

$$(R_1 + {\rm j} \cdot I_1) (R_2 + {\rm j} \cdot I_2) = (R_1 \cdot R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot I_1)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{A_{\rm M} = 2,\hspace{0.3cm}M_{\rm M} = 4} \hspace{0.05cm}.$$

(3)  The basic operations with complex inputs  $E_1$,  $E_2$  and  $w^{\hspace{0.04cm}\mu}$ are:

$$A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu},\hspace{0.5cm} A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$

• This means one complex multiplication and two complex additions:   $\hspace{0.15 cm}\underline{a_{\rm B} = 2, \hspace{0.2cm}m_{\rm B} = 1} \hspace{0.05cm}.$

(4)  In contrast to the first computers, a multiplication today does not take much more computing time than an addition or subtraction.

• Using the results of subtasks  (1),  (2)  and  (3)  we obtain for the total number of arithmetic operations:

$$\mathcal{O}_{\rm B} = a_{\rm B}\cdot A_{\rm A} + a_{\rm B}\cdot (A_{\rm M} +M_{\rm M} ) = 2 \cdot 2 + 1 \cdot 6\hspace{0.15 cm}\underline{ = 10} \hspace{0.05cm}.$$

(5)  There are  ${\rm log_2} \ N$ stages in total, each of which requires  $N/2$  basic operations to be performed:

$$\mathcal{O}_{\rm FFT} = {\rm log_2}\hspace{0.1cm}N \cdot \frac{N}{2}\cdot \mathcal{O}_{\rm B} = 5 \cdot N \cdot {\rm log_2}\hspace{0.1cm}N$$

$$\Rightarrow \hspace{0.3cm}\mathcal{O}_{\rm FFT}\hspace{0.1cm}(N=16) = 5\cdot 16 \cdot 4 \hspace{0.15 cm}\underline{= 320}, \hspace{0.5cm}\mathcal{O}_{\rm FFT}\hspace{0.1cm}(N=1024) = 5\cdot 1024 \cdot 10 \hspace{0.15 cm}\underline{= 51200} \hspace{0.05cm}.$$

(6)  The computational time gain of the FFT over the conventional DFT is given by:

$$G_{\rm FFT} = \frac{\mathcal{O}_{\rm DFT}}{\mathcal{O}_{\rm FFT}} = \frac{8 \cdot N^2} {5 \cdot N \cdot {\rm log_2}\hspace{0.1cm}N }= 1.6 \cdot \frac{N}{ {\rm log_2}\hspace{0.1cm}N}$$

$$\Rightarrow \hspace{0.3cm}G_{\rm FFT} \hspace{0.1cm}(N=16) = 1.6 \cdot \frac{16}{ 4} \hspace{0.15 cm}\underline{= 6.4}, \hspace{0.5cm}G_{\rm FFT} \hspace{0.1cm}(N=1024) = 1.6 \cdot\frac{1024}{ 10}\hspace{0.15 cm}\underline{ \approx 164} \hspace{0.05cm}.$$