Aufgaben:Exercise 4.9: Higher-Level Modulation

• Return to book

Einige Kanalkapazitätskurven

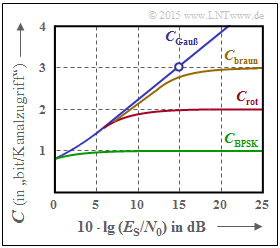
Die Grafik zeigt AWGN–Kanalkapazitätskurven über der Abszisse  $10 \cdot \lg (E_{\rm S}/{N_0})$:

• $C_\text{Gauß}$:    Shannonsche Grenzkurve,
• $C_\text{BPSK}$:    gültig für Binary Phase Shift Keying.

Die beiden weiteren Kurvenverläufe  $C_\text{rot}$  und  $C_\text{braun}$  sollen in den Teilaufgaben  (3)  und  (4)  analysiert und möglichen Modulationsverfahren zugeordnet werden.

Hinweise:

• Die Aufgabe gehört zum Kapitel  AWGN–Kanalkapazität bei wertdiskretem Eingang.
• Bezug genommen wird insbesondere auf die Seite  Die Kanalkapazität $C$ als Funktion von $E_{\rm S}/{N_0}$.
• Da die Ergebnisse in "bit" angegeben werden sollen, wird in den Gleichungen "log"  ⇒  "log₂" verwendet.
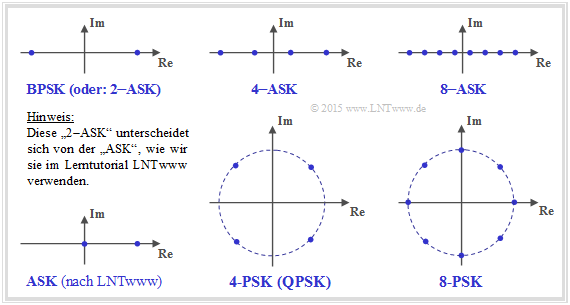
• Die im Fragebogen genannten Modulationsverfahren werden anhand ihrer Signalraumkonstellation beschrieben:

Vorgeschlagene Signalraumkonstellationen

Anmerkungen zur Nomenklatur:

• In der Literatur wird manchmal die "BPSK" auch mit "2–ASK" bezeichnet

$$x ∈ X = \{+1,\ -1\}.$$

• Dagegen verstehen wir in unserem Lerntutorial $\rm LNTwww$ als "ASK" den unipolaren Fall

$$x ∈ X = \{0,\ 1 \}.$$

• Nach unserer Nomenklatur gilt deshalb:

$$C_\text{AK} < C_\text{BPSK}$$

Dieser Sachverhalt ist unerheblich für die Lösung der vorliegenden Aufgabe.

Fragebogen

1

Welche Gleichung liegt der Shannon–Grenzkurve  $C_{\rm Gauß}$  zugrunde?

	Es gilt   $C_{\rm Gauß} = C_1= {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + E_{\rm S}/{N_0})$ ,
	Es gilt   $C_{\rm Gauß} = C_2= {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot E_{\rm S}/{N_0})$ ,
	Es gilt   $C_{\rm Gauß} = C_3= {\rm log}_2 \hspace{0.1cm} ( 1 + E_{\rm S}/{N_0})$ .

2

Welche Aussagen treffen für die grüne Kurve  $C_{\rm BPSK}$  zu?

	$C_{\rm BPSK}$  kann nicht in geschlossener Form angegeben werden.
	$C_{\rm BPSK}$  ist größer als Null, wenn  $E_{\rm S}/{N_0} > 0$  vorausgesetzt wird.
	Für  $E_{\rm S}/{N_0} < \ln (2)$  ist  $C_{\rm BPSK} ≡ 0$.
	Im gesamten Bereich gilt  $C_{\rm BPSK} < C_{\rm Gauß}$.

3

Welche Aussagen treffen für die rote Kurve  $C_{\rm rot}$  zu?

	Für die zugehörige Zufallsgröße  $X$  gilt  $M_X = |X| = 2$.
	Für die zugehörige Zufallsgröße  $X$  gilt  $M_X = |X| = 4$.
	$C_{\rm rot}$  ist gleichzeitig die Kanalkapazität der 4–ASK.
	$C_{\rm rot}$  ist gleichzeitig die Kanalkapazität der 4–QAM.
	Für alle  $E_{\rm S}/{N_0} > 0$  liegt  $C_{\rm rot}$  zwischen "grün" und "braun".

4

Welche Aussagen treffen für die braune Kurve  $C_{\rm braun}$  zu?  ($p_{\rm B}$:   Bitfehlerwahrscheinlichkeit)

	Für die zugehörige Zufallsgröße  $X$  gilt  $M_X = |X| = 8$.
	$C_{\rm braun}$  ist gleichzeitig die Kanalkapazität der 8–ASK.
	$C_{\rm braun}$  ist gleichzeitig die Kanalkapazität der 8–PSK.
	$p_{\rm B} ≡ 0$  ist mit 8–ASK,  $R = 2.5$  und  $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$  möglich.
	$p_{\rm B} ≡ 0$  ist mit 8–ASK,  $R = 2$  und  $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$  möglich.

Musterlösung

Solution

(1)  Richtig ist der Vorschlag 2, wie die Rechnung für  $10 \cdot \lg (E_{\rm S}/{N_0}) = 15 \ \rm dB$   ⇒   $E_{\rm S}/{N_0} = 31.62$ zeigt:

$$C_2(15\hspace{0.1cm}{\rm dB}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot 31.62 ) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 64.25 ) \approx 3\,{\rm bit/Kanalzugriff}\hspace{0.05cm}.$$

• Die beiden anderen Lösungsvorschläge liefern folgende Zahlenwerte:

$$C_3(15\hspace{0.1cm}{\rm dB}) \ = \ {\rm log}_2 \hspace{0.1cm} ( 1 + 31.62 ) \approx 5.03\,{\rm bit/Kanalzugriff}\hspace{0.05cm},$$

$$C_1(15\hspace{0.1cm}{\rm dB}) \ = \ C_3/2 \approx 2.51\,{\rm bit/Kanalzugriff}\hspace{0.05cm}.$$

• Der Lösungsvorschlag 3 entspricht dabei dem Fall Zweier unabhängiger Gaußkanäle mit jeweils halber Sendeleistung pro Kanal.

(2)  Richtig sind die Lösungsvorschläge 1, 2 und 4:

• Würde man  $E_{\rm S}$  durch  $E_{\rm B}$  ersetzen, so wäre auch die Aussage 3 richtig.
• Für  $E_{\rm B}/{N_0} < \ln (2)$  gilt nämlich  $C_{\rm Gauß} ≡ 0$  und damit auch  $C_{\rm BPSK} ≡ 0$ .

(3)  Richtig sind die Aussagen 2, 3 und 5:

• Der rote Kurvenzug  $C_{\rm rot}$  liegt stets oberhalb von  $C_{\rm BPSK}$ , aber unterhalb von  $C_{\rm braun}$  und der Shannon–Grenzkurve  $C_{\rm Gauß}$.
• Die Aussagen gelten auch, wenn für gewisse  $E_{\rm S}/{N_0}$–Werte Kurven innerhalb der Zeichengenauigkeit nicht zu unterscheiden sind.
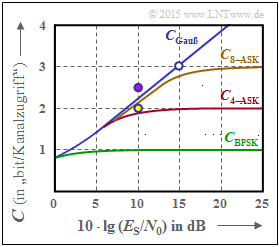
• Aus dem Grenzwert  $C_{\rm rot}= 2 \ \rm bit/Kanalzugriff$  für  $E_{\rm S}/{N_0} → ∞$  ergibt sich der Symbolumfang  $M_X = |X| = 4$.
• Die rote Kurve beschreibt also die 4–ASK.  $M_X = |X| = 2$  würde für die BPSK gelten.
• Die 4–QAM führt genau zum gleichen Endwert "2 bit/Kanalzugriff".  Für kleine  $E_{\rm S}/{N_0}$–Werte liegt aber die Kanalkapazität  $C_{\rm 4–QAM}$  oberhalb der roten Kurve, da  $C_{\rm rot}$  von der Gauß–Grenzkurve  $C_2$  begrenzt wird, $C_{\rm 4–QAM}$  aber von  $C_3$.

Die Bezeichnungen  $C_2$  und  $C_3$  beziehen sich hierbei auf die Teilaufgabe  (1).

Kanalkapazitätsgrenzen für
BPSK, 4–ASK und 8–ASK

(4)  Richtig sind die Lösungsvorschläge 1, 2 und 5:

• Aus dem braunen Kurvenverlauf erkennt man die Richtigkeit der beiden ersten Aussagen.
• Die 8–PSK mit I– und Q–Komponente – also mit  $K = 2$  Dimensionen – liegt für kleine  $E_{\rm S}/{N_0}$–Werte etwas oberhalb der braunen Kurve   ⇒   die Antwort 3 ist falsch.

In der Grafik sind auch die beiden 8–ASK–Systeme gemäß den Vorschlägen 4 und 5 als Punkte eingezeichnet.

• Der violette Punkt liegt über der Kurve  $C_{\rm 8–ASK}$   ⇒   $R = 2.5$ und $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$ reichen nicht aus, um die 8–ASK fehlerfrei decodieren zu können   ⇒   $R > C$   ⇒   das Kanalcodierungstheorem wird nicht erfüllt   ⇒   Antwort 4 ist falsch.
• Reduziert man aber die Coderate gemäß dem gelben Punkt bei gleichem $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$ auf $R = 2 < C_{\rm 8–ASK}$, so wird das Kanalcodierungstheorem erfüllt   ⇒   Antwort 5 ist richtig.