Difference between revisions of "Aufgaben:Exercise 3.3: Entropy of Ternary Quantities"
From LNTwww
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID2754__Inf_A_3_3.png|right|frame| | + | [[File:P_ID2754__Inf_A_3_3.png|right|frame|Given entropy functions]] |
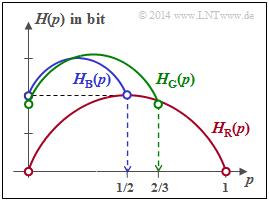
| − | + | On the right you see the entropy functions $H_{\rm R}(p)$, $H_{\rm B}(p)$ and $H_{\rm G}(p)$, where $\rm R$ stands for "red", $\rm B$ for "blue" and $\rm G$ for "green". The probability functions are for all random variables: | |
:$$P_X(X) = [\hspace{0.05cm}p_1\hspace{0.05cm},\ p_2\hspace{0.05cm},\ p_3\hspace{0.05cm}]\hspace{0.3cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} |X| = 3\hspace{0.05cm}.$$ | :$$P_X(X) = [\hspace{0.05cm}p_1\hspace{0.05cm},\ p_2\hspace{0.05cm},\ p_3\hspace{0.05cm}]\hspace{0.3cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} |X| = 3\hspace{0.05cm}.$$ | ||
| − | + | For the questionnaire, the relationship $p_1 = p$ and $p_2 = 1 - p_3- p$. | |
| − | + | The probability function of a random variable | |
:$$X = \big \{\hspace{0.05cm}x_1\hspace{0.05cm}, \hspace{0.15cm} x_2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} x_{\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm} , \hspace{0.15cm} x_{M}\hspace{0.05cm}\big \}$$ | :$$X = \big \{\hspace{0.05cm}x_1\hspace{0.05cm}, \hspace{0.15cm} x_2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} x_{\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm} , \hspace{0.15cm} x_{M}\hspace{0.05cm}\big \}$$ | ||
| − | + | with the symbolic range $|X| = M$ is generally: | |
:$$P_X(X) = [\hspace{0.05cm}p_1\hspace{0.05cm}, \hspace{0.15cm} p_2\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.1cm} ,\hspace{0.15cm} p_{\mu}\hspace{0.05cm}, \hspace{0.05cm}...\hspace{0.1cm} , \hspace{0.15cm} p_{M}\hspace{0.05cm}]\hspace{0.05cm}.$$ | :$$P_X(X) = [\hspace{0.05cm}p_1\hspace{0.05cm}, \hspace{0.15cm} p_2\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.1cm} ,\hspace{0.15cm} p_{\mu}\hspace{0.05cm}, \hspace{0.05cm}...\hspace{0.1cm} , \hspace{0.15cm} p_{M}\hspace{0.05cm}]\hspace{0.05cm}.$$ | ||
| − | + | The entropy (uncertainty) of this random variable is calculated according to the equation | |
:$$H(X) = {\rm E} \big [\log_2 \hspace{0.05cm} {1}/{P_X(X)} \big ]\hspace{0.05cm},$$ | :$$H(X) = {\rm E} \big [\log_2 \hspace{0.05cm} {1}/{P_X(X)} \big ]\hspace{0.05cm},$$ | ||
| − | + | and always lies in the range $0 \le H(X) \le \log_2 \hspace{0.05cm} |X|$. | |
| − | * | + | *The lower bound $H(X) = 0$ results when any probability $p_\mu = 1$ and all others are zero. |
| − | * | + | *The upper bound is to be derived here as in the lecture "Information Theory" by [[Biographies_and_Bibliographies/Lehrstuhlinhaber_des_LNT#Prof._Dr._sc._techn._Gerhard_Kramer_.28seit_2010.29|Gerhard Kramer]] at the TU Munich: |
| − | [[File:P_ID2755__Inf_A_3_3_B_neu.png|right|frame| | + | [[File:P_ID2755__Inf_A_3_3_B_neu.png|right|frame|Upper bound estimate for the natural logarithm]] |
| − | :* | + | :* By extending the above equation by $|X|$ in the numerator and denominator, using $\log_2 \hspace{0.05cm}x= \ln(x)/\ln(2)$, we obtain: |
::$$H(X) = \frac{1}{{\rm ln}(2)}\cdot {\rm E} \left [{\rm ln} \hspace{0.1cm} \frac{1}{|X| \cdot P_X(X)} \right ] + {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$ | ::$$H(X) = \frac{1}{{\rm ln}(2)}\cdot {\rm E} \left [{\rm ln} \hspace{0.1cm} \frac{1}{|X| \cdot P_X(X)} \right ] + {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$ | ||
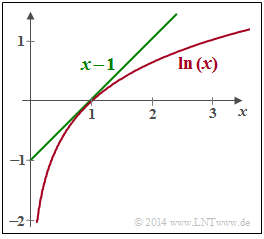
| − | :* | + | :* As can be seen from the graph opposite, the estimation $\ln(x) \le x-1$ holds with the identity for $x=1$. Thus, it can be written: |
::$$H(X) \le \frac{1}{{\rm ln}(2)}\cdot {\rm E} \left [\frac{1}{|X| \cdot P_X(X)} -1 \right ] + {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$ | ::$$H(X) \le \frac{1}{{\rm ln}(2)}\cdot {\rm E} \left [\frac{1}{|X| \cdot P_X(X)} -1 \right ] + {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$ | ||
| − | :* In | + | :* In [[Aufgaben:3.2_Erwartungswertberechnungen|exercise 3.2]] the expected value ${\rm E} \big [\log_2 \hspace{0.05cm} {1}/{P_X(X)} \big ] =|X|$ was calculated for the case $p_\mu \ne 0$ for all $\mu$ . Thus, the first term disappears and the known result is obtained: |
::$$H(X) \le {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$ | ::$$H(X) \le {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$ | ||
| Line 32: | Line 32: | ||
| − | + | Hints: | |
*Die Aufgabe gehört zum Kapitel [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen|Einige Vorbemerkungen zu den 2D-Zufallsgrößen]]. | *Die Aufgabe gehört zum Kapitel [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen|Einige Vorbemerkungen zu den 2D-Zufallsgrößen]]. | ||
*Insbesondere wird Bezug genommen auf die Seite [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Wahrscheinlichkeitsfunktion_und_Entropie|Wahrscheinlichkeitsfunktion undEntropie]]. | *Insbesondere wird Bezug genommen auf die Seite [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Wahrscheinlichkeitsfunktion_und_Entropie|Wahrscheinlichkeitsfunktion undEntropie]]. | ||
Revision as of 13:46, 19 August 2021
On the right you see the entropy functions $H_{\rm R}(p)$, $H_{\rm B}(p)$ and $H_{\rm G}(p)$, where $\rm R$ stands for "red", $\rm B$ for "blue" and $\rm G$ for "green". The probability functions are for all random variables:
- $$P_X(X) = [\hspace{0.05cm}p_1\hspace{0.05cm},\ p_2\hspace{0.05cm},\ p_3\hspace{0.05cm}]\hspace{0.3cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} |X| = 3\hspace{0.05cm}.$$
For the questionnaire, the relationship $p_1 = p$ and $p_2 = 1 - p_3- p$.
The probability function of a random variable
- $$X = \big \{\hspace{0.05cm}x_1\hspace{0.05cm}, \hspace{0.15cm} x_2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} x_{\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm} , \hspace{0.15cm} x_{M}\hspace{0.05cm}\big \}$$
with the symbolic range $|X| = M$ is generally:
- $$P_X(X) = [\hspace{0.05cm}p_1\hspace{0.05cm}, \hspace{0.15cm} p_2\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.1cm} ,\hspace{0.15cm} p_{\mu}\hspace{0.05cm}, \hspace{0.05cm}...\hspace{0.1cm} , \hspace{0.15cm} p_{M}\hspace{0.05cm}]\hspace{0.05cm}.$$
The entropy (uncertainty) of this random variable is calculated according to the equation
- $$H(X) = {\rm E} \big [\log_2 \hspace{0.05cm} {1}/{P_X(X)} \big ]\hspace{0.05cm},$$
and always lies in the range $0 \le H(X) \le \log_2 \hspace{0.05cm} |X|$.
- The lower bound $H(X) = 0$ results when any probability $p_\mu = 1$ and all others are zero.
- The upper bound is to be derived here as in the lecture "Information Theory" by Gerhard Kramer at the TU Munich:
- By extending the above equation by $|X|$ in the numerator and denominator, using $\log_2 \hspace{0.05cm}x= \ln(x)/\ln(2)$, we obtain:
- $$H(X) = \frac{1}{{\rm ln}(2)}\cdot {\rm E} \left [{\rm ln} \hspace{0.1cm} \frac{1}{|X| \cdot P_X(X)} \right ] + {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$
- As can be seen from the graph opposite, the estimation $\ln(x) \le x-1$ holds with the identity for $x=1$. Thus, it can be written:
- $$H(X) \le \frac{1}{{\rm ln}(2)}\cdot {\rm E} \left [\frac{1}{|X| \cdot P_X(X)} -1 \right ] + {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$
- In exercise 3.2 the expected value ${\rm E} \big [\log_2 \hspace{0.05cm} {1}/{P_X(X)} \big ] =|X|$ was calculated for the case $p_\mu \ne 0$ for all $\mu$ . Thus, the first term disappears and the known result is obtained:
- $$H(X) \le {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$
Hints:
- Die Aufgabe gehört zum Kapitel Einige Vorbemerkungen zu den 2D-Zufallsgrößen.
- Insbesondere wird Bezug genommen auf die Seite Wahrscheinlichkeitsfunktion undEntropie.
- Ausgegangen wird hier von der gleichen Konstellation wie in der Aufgabe 3.2.
- Die Gleichung der binären Entropiefunktion lautet:
- $$H_{\rm bin}(p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1) Beide Aussagen sind richtig:
- Setzt man $p_3 = 0$ und formal $p_1 = p$ ⇒ $p_2 = 1- p$, so ergibt sich die binäre Entropiefunktion
- $$H_{\rm bin}(p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p} \hspace{0.05cm}.$$
(2) Richtig ist allein der Lösungsvorschlag 1:
- Man kann die binäre Entropiefunktion wegen $\log(x) = \ln(x)/\ln(2)$ auch in die folgende Form bringen:
- $$H_{\rm bin}(p) = \frac{-1}{{\rm ln}(2)} \cdot \big [ p \cdot {\rm ln}(p) + (1-p) \cdot {\rm ln}(1-p) \big ] \hspace{0.05cm}.$$
- Die erste Ableitung führt zum Ergebnis
- $$\frac {{\rm d}H_{\rm bin}(p)}{{\rm d}p} = \frac{-1}{{\rm ln}(2)} \cdot \big [ {\rm ln}(p) + p \cdot \frac{1}{p} - {\rm ln}(1-p) - (1-p) \cdot \frac{1}{1-p} \big ] = \frac{1}{{\rm ln}(2)} \cdot \big [ {\rm ln}(1-p) - {\rm ln}(p) \big ] = {\rm log}_2 \hspace{0.1cm} \frac{1-p}{p} \hspace{0.05cm}.$$
- Durch Nullsetzen dieser Ableitung erhält man den Abszissenwert $p = 0.5$, der zum Maximum der Entropiefunktion führt: $H_{\rm bin}(p =0.5) = 1$ bit
⇒ der Lösungsvorschlag 2 ist falsch. - Durch nochmaliges Differenzieren erhält man für die zweite Ableitung:
- $$\frac {{\rm d}^2H_{\rm bin}(p)}{{\rm d}p^2} = \frac{1}{{\rm ln}(2)} \cdot \left [ \frac{-1}{1-p} - \frac{1}{p} \right ] = \frac{-1}{{\rm ln}(2) \cdot p \cdot (1-p)} \hspace{0.05cm}.$$
- Diese Funktion ist im gesamten Definitionsgebiet $0 ≤ p ≤ 1$ negativ ⇒ $H_{\rm bin}(p)$ ist konkav ⇒ der Lösungsvorschlag 1 ist richtig.
(3) Richtig sind hier die Aussagen 1 und 2:
- Für $p = 0$ erhält man die Wahrscheinlichkeitsfunktion $P_X(X) = \big [\hspace{0.05cm}0\hspace{0.05cm}, \hspace{0.15cm} 1/2\hspace{0.05cm},\hspace{0.15cm} 1/2 \hspace{0.05cm} \big ]$ ⇒ $H(X) = 1$ bit.
- Das Maximum unter der Voraussetzung $p_3 = 1/2$ ergibt sich für $p_1 = p_2 = 1/4$:
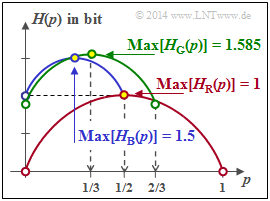
- $$P_X(X) = \big [\hspace{0.05cm}1/4\hspace{0.05cm}, \hspace{0.05cm} 1/4\hspace{0.05cm},\hspace{0.05cm} 1/2 \hspace{0.05cm} \big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Max} \ [H_{\rm B}(p)] = 1.5 \ \rm bit \hspace{0.05cm}.$$
- In kompakter Form lässt sich $H_{\rm B}(p)$ mit der Einschränkung $0 ≤ p ≤ 1/2$ wie folgt darstellen:
- $$H_{\rm B}(p) = 1.0\,{\rm bit} + {1}/{2} \cdot H_{\rm bin}(2p) \hspace{0.05cm}.$$
(4) Richtig sind hier die erste und letzte Aussage:
- Der grüne Kurvenzug beinhaltet mit $p = 1/3$ auch die Gleichverteilung aller Wahrscheinlichkeiten
- $$ {\rm Max} \ [H_{\rm G}(p)] = \log_2 (3)\ \text{bit}.$$
- Allgemein lässt sich der gesamte Kurvenverlauf im Bereich $0 ≤ p ≤ 2/3$ wie folgt ausdrücken:
- $$H_{\rm G}(p) = H_{\rm G}(p= 0) + {2}/{3} \cdot H_{\rm bin}(3p/2) \hspace{0.05cm}.$$
- Aus der Grafik auf der Angabenseite erkennt man auch, dass folgende Bedingung erfüllt sein muss:
- $$H_{\rm G}(p = 0) + {2}/{3}= {\rm log}_2 \hspace{0.01cm} (3) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm G}(p= 0) = 1.585 - 0.667 = 0.918 \,{\rm bit} \hspace{0.05cm}.$$
- Der zweite Lösungsvorschlag ist somit falsch. Zum gleichen Ergebnis gelangt man über die Gleichung
- $$H_{\rm G}(p = 0) = {1}/{3} \cdot {\rm log}_2 \hspace{0.01cm} (3) +{2}/{3} \cdot {\rm log}_2 \hspace{0.01cm} (3/2) = {\rm log}_2 \hspace{0.01cm} (3) -2/3 \cdot {\rm log}_2 \hspace{0.01cm} (2) \hspace{0.05cm}.$$