Aufgaben:Exercise 4.4: Conventional Entropy and Differential Entropy

• Return to book

Two uniform distributions

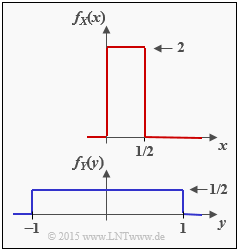
We consider the two continuous random variables  $X$  and  $Y$  with probability density functions $f_X(x)$  and $f_Y(y)$.  For these random variables one can

• not specify the conventional entropies  $H(X)$  and  $H(Y)$ , respectively,
• but the differential entropies  $h(X)$  and  $h(Y)$.

We also consider two value-discrete random variables:

• The variable  $Z_{X,\hspace{0.05cm}M}$  is obtained by (suitably) quantizing the random quantity  $X$ with the quantization level number  $M$
  ⇒   quantization interval width  ${\it \Delta} = 0.5/M$.
• The variable  $Z_{Y,\hspace{0.05cm}M}$  is obtained after quantization of the random quantity  $Y$  with the quantization level number  $M$  
  ⇒   quantization interval width  ${\it \Delta} = 2/M$.

The probability density functions  $\rm (PDF)$  of these discrete random variables are each composed of  $M$  Dirac functions whose momentum weights are given by the interval areas of the associated continuous random variables.

From this, the entropies  $H(Z_{X,\hspace{0.05cm}M})$  and  $H(Z_{Y,\hspace{0.05cm}M})$  can be determined in the conventional way according to the page  Probability mass function and entropy .

In the section  Entropy of value-ontinuous random variables after quantization,  an approximation was also given.  For example:

$$H(Z_{X, \hspace{0.05cm}M}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X)\hspace{0.05cm}. $$

• In the course of the task it will be shown that in the case of rectangular PDF   ⇒   uniform distribution this  "approximation"  gives the same result as the direct calculation.
• But in the general case – so in  $\text{Example 2}$  with triangular PDF – this equation is in fact only an approximation, which agrees with the actual entropy  $H(Z_{X,\hspace{0.05cm}M})$  only in the limiting case   ${\it \Delta} \to 0$ .

Hints:

• The exercise belongs to the chapter  Differential Entropy.
• Useful hints for solving this task can be found in particular on the page  Entropy of continuous random variables after quantization.

Questions

1

Calculate the differential entropy  $h(X)$.

$ h(X) \ = \ $ $\ \rm bit$

2

Calculate the differential entropy $h(Y)$.

$ h(Y) \ = \ $ $\ \rm bit$

3

Calculate the entropy of the value-discrete random variables  $Z_{X,\hspace{0.05cm}M=4}$  using the direct method.

$H(Z_{X,\hspace{0.05cm}M=4})\ = \ $ $\ \rm bit$

4

Calculate the entropy of the value-discrete random variables  $Z_{X,\hspace{0.05cm}M=4}$  using the given approximation.

$H(Z_{X,\hspace{0.05cm}M=4})\ = \ $ $\ \rm bit$

5

Calculate the entropy of the value-discrete random variable  $Z_{Y,\hspace{0.05cm}M=8}$  with the given approximation.

$H(Z_{Y,\hspace{0.05cm}M=8})\ = \ $ $\ \rm bit$

6

Which of the following statements are true?

	The entropy of a discrete value random variable  $Z$  is always  $H(Z) \ge 0$.
	The differential entropy of a continuous value random variable  $X$  is always  $h(X) \ge 0$.

Solution

Solution

(1)  According to the corresponding theory page, with  $x_{\rm min} = 0$  and  $x_{\rm max} = 1/2$:

$$h(X) = {\rm log}_2 \hspace{0.1cm} (x_{\rm max} - x_{\rm min}) = {\rm log}_2 \hspace{0.1cm} (1/2) \hspace{0.15cm}\underline{= - 1\,{\rm bit}}\hspace{0.05cm}.$$

(2)  On the other hand, with  $y_{\rm min} = -1$  and  $y_{\rm max} = +1$  the differential entropy of the random variable  $Y$ is given by:

$$h(Y) = {\rm log}_2 \hspace{0.1cm} (y_{\rm max} - y_{\rm min}) = {\rm log}_2 \hspace{0.1cm} (2) \hspace{0.15cm}\underline{= + 1\,{\rm bit}}\hspace{0.05cm}. $$

Quantized random variable  $Z_{X, \ M = 4}$

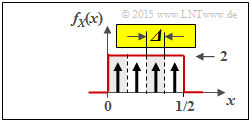
(3)  The adjacent graph illustrates the best possible quantization of random variable  $X$  with quantization level number  $M = 4$    ⇒   random variable  $Z_{X, \ M = 4}$:

• The interval width here is equal to  ${\it \Delta} = 0.5/4 = 1/8$.
• The possible values  (at the center of the interval,  respectively)  are  $z \in \{0.0625,\ 0.1875,\ 0.3125,\ 0.4375\}$.

Using the probability mass function, the direct entropy calculation gives $P_Z(Z) = \big [1/4,\ \text{...} , \ 1/4 \big]$:

$$H(Z_{X, \ M = 4}) = {\rm log}_2 \hspace{0.1cm} (4) \hspace{0.15cm}\underline{= 2\,{\rm bit}} \hspace{0.05cm}.$$

With the approximation, considering the result of  (1), we obtain:

$$H(Z_{X,\hspace{0.05cm} M = 4}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X) = 3\,{\rm bit} +(- 1\,{\rm bit})\hspace{0.15cm}\underline{= 2\,{\rm bit}}\hspace{0.05cm}. $$

Note:  Only in the case of uniform distribution, the approximation gives exactly the same result as the direct calculation, i.e. the actual entropy.

Quantized random variable $Z_{Y, \ M = 4}$

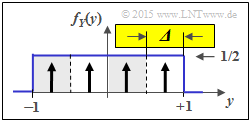
(4)  From the second graph, one can see the similarities / differences to subtask  (3):

• The quantization parameter is now  ${\it \Delta} = 2/4 = 1/2$.
• The possible values are now  $z \in \{\pm 0.75,\ \pm 0.25\}$.
• Thus, here the  "approximation"  (as well as the direct calculation)  gives the result:

$$H(Z_{Y,\hspace{0.05cm} M = 4}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(Y) = 1\,{\rm bit} + 1\,{\rm bit}\hspace{0.15cm}\underline{= 2\,{\rm bit}}\hspace{0.05cm}.$$

Quantized random variable  $Z_{Y, \ M = 8}$

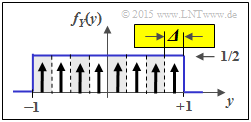
(5)  In contrast to subtask  (5):   ${\it \Delta} = 1/4$  is now valid.  From this follows for the "approximation":

$$H(Z_{Y,\hspace{0.05cm} M = 8}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(Y) = 2\,{\rm bit} + 1\,{\rm bit}\hspace{0.15cm}\underline{= 3\,{\rm bit}}\hspace{0.05cm}.$$

Again, one gets the same result as in the direct calculation.

(6)  Only statement 1  is correct:

• The entropy  $H(Z)$  of a value-discrete random variable  $Z = \{z_1, \ \text{...} \ , z_M\}$  is never negative.
• For example, the limiting case  $H(Z) = 0$  results for  ${\rm Pr}(Z = z_1) = 1$  and  ${\rm Pr}(Z = z_\mu) = 0$  for  $2 \le \mu \le M$.

• In contrast, the differential entropy  $h(X)$  of a continuous value random variable  $X$  can be as follows:
  • $h(X) < 0$  $($subtask 1$)$,
  • $h(X) > 0$  $($subtask 2$)$, or even
  • $h(X) = 0$  $($for example fo  $x_{\rm min} = 0$  and  $x_{\rm max} = 1)$.