Difference between revisions of "Aufgaben:Exercise 3.4: Attenuation and Phase Response"
From LNTwww
| Line 50: | Line 50: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Compute $H(f)$. What is its magnitude at very large frequencies? |
|type="{}"} | |type="{}"} | ||
$|H(f → ∞)| \ = \ $ { 0. } | $|H(f → ∞)| \ = \ $ { 0. } | ||
| − | { | + | {Compute the magnitude frequency response and the attenuation value for $f → 0$. |
|type="{}"} | |type="{}"} | ||
$|H(f = 0)| \ = \ $ { 0.278 3% } | $|H(f = 0)| \ = \ $ { 0.278 3% } | ||
| Line 61: | Line 61: | ||
| − | { | + | {Compute the attenuation value at $f =4/(2 \pi)$ in neper $\rm(Np)$ and decibel $\rm(dB)$ according to the described approach. |
|type="{}"} | |type="{}"} | ||
$a(f = 2/ \pi)\ = \ $ { 0.155 3% } $\ \rm Np$ | $a(f = 2/ \pi)\ = \ $ { 0.155 3% } $\ \rm Np$ | ||
| Line 67: | Line 67: | ||
| − | { | + | {Compute the phase value at frequency $f = 4/(2 \pi)$ according to the described approach. |
|type="{}"} | |type="{}"} | ||
$b(f = 2/ \pi)\ = \ $ { -19.3--18.3 } $\ \rm Grad$ | $b(f = 2/ \pi)\ = \ $ { -19.3--18.3 } $\ \rm Grad$ | ||
| Line 77: | Line 77: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The $p$–transfer function is: |
:$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} | :$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} | ||
{(p - p_{\rm x 1})(p - p_{\rm x 2})} | {(p - p_{\rm x 1})(p - p_{\rm x 2})} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *The conventional transfer function (the frequency response) is obtained via the substitution $p = {\rm j} \cdot 2 \pi f$: |
:$$H(f)= K \cdot \frac {{\rm j \hspace{0.05cm}2\pi \it | :$$H(f)= K \cdot \frac {{\rm j \hspace{0.05cm}2\pi \it | ||
f} - p_{\rm o }} | f} - p_{\rm o }} | ||
| Line 91: | Line 91: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *In the limiting case $f → \infty$ the following is obtained for the magnitude, attenuation and phase: |
:$$\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} H(f)= \frac{K}{{\rm j \hspace{0.05cm}2\pi \it | :$$\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} H(f)= \frac{K}{{\rm j \hspace{0.05cm}2\pi \it | ||
f}}\hspace{0.15cm}\Rightarrow \hspace{0.15cm}\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} |H(f)|\hspace{0.15cm}\underline {= 0} \hspace{0.05cm} | f}}\hspace{0.15cm}\Rightarrow \hspace{0.15cm}\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} |H(f)|\hspace{0.15cm}\underline {= 0} \hspace{0.05cm} | ||
| Line 101: | Line 101: | ||
| − | '''(2)''' | + | '''(2)''' From the general equation in subtask '''(1)''' the following is obtained with the limit process $f → 0$: |
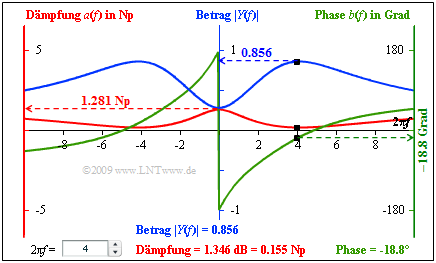
| − | [[File:P_ID1769__LZI_A_3_4_d_neu.png|right|frame|$|H(f)|$, $a(f)$ | + | [[File:P_ID1769__LZI_A_3_4_d_neu.png|right|frame|$|H(f)|$, $a(f)$ and $b(f)$]] |
:$$|H(f=0)|= -\frac {K \cdot p_{\rm o }} | :$$|H(f=0)|= -\frac {K \cdot p_{\rm o }} | ||
{p_{\rm x 1}\cdot p_{\rm x 2}} | {p_{\rm x 1}\cdot p_{\rm x 2}} | ||
| Line 112: | Line 112: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | The screen capture of the Flash–module "Causal Systems" summarizes the results of this exercise: | |
| − | :* | + | :*middle axis (blue): magnitude $|H(f)|$, |
| − | :* | + | :*left axis (red): attenuation $a(f)$, |
| − | :* | + | :*right axis (green): phase $b(f)$. |
| − | :* | + | :*black point: values for $2\pi f = 4.$ |
<br clear=all> | <br clear=all> | ||
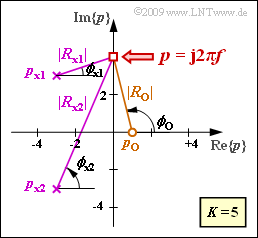
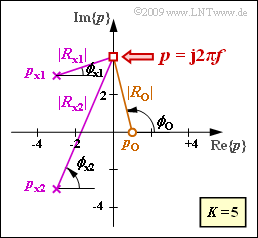
| − | [[File:P_ID2843__LZI_A_3_4.png|right|frame| | + | [[File:P_ID2843__LZI_A_3_4.png|right|frame|Pole-zero diagram and some auxiliary quantities]]] |
'''(3)''' Entsprechend der detaillierten Beschreibung im [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function#Graphical_determination_of_attenuation_and_phase|Theorieteil]] gilt für die Dämpfungsfunktion: | '''(3)''' Entsprechend der detaillierten Beschreibung im [[Linear_and_Time_Invariant_Systems/Laplace_Transform_and_p-Transfer_Function#Graphical_determination_of_attenuation_and_phase|Theorieteil]] gilt für die Dämpfungsfunktion: | ||
Revision as of 16:42, 12 October 2021
Pole-zero diagram and definition of some auxiliary quantities
We assume the sketched pole–zero diagram, i.e. the values
- $$K = 5, \hspace{0,2cm}Z = 1, \hspace{0,2cm}N = 2, $$
- $$ p_{\rm o}= 1,\hspace{0,2cm}p_{\rm x1}= -3 + 3{\rm j},\hspace{0,2cm}p_{\rm x2}= -3 - 3{\rm j}\hspace{0.05cm} .$$
Thus, the $p$–transfer function is:
- $$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$
Considering the substitution $p = {\rm j} \cdot 2 \pi f$, the conventional transfer function can be specified, which is also called frequency response:
- $$H(f) = H_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it f}} = {\rm e}^{-a(f)\hspace{0.05cm}}\cdot {\rm e}^{- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.05cm}.$$
From this equation, the relationship between
- the transfer function $H(f)$,
- the attenuation function $a(f)$ and
- the phase function $b(f)$
can also be seen.
The attenuation and phase values can be determined as follows for a frequency $f$ indirectly specified by the point $p = {\rm j} \cdot 2 \pi f$ :
- $$a(f)\hspace{0.15cm}{\rm in}\hspace{0.15cm}{\rm Np} \hspace{0.25cm} = \hspace{0.2cm} -{\rm ln} \hspace{0.1cm} K + {\rm ln} \hspace{0.1cm} |R_{\rm x1}|+{\rm ln} \hspace{0.1cm} |R_{\rm x1}|- {\rm ln} \hspace{0.1cm} |R_{{\rm o} }|\hspace{0.05cm} ,$$
- $$ b(f)\hspace{0.15cm}{\rm in}\hspace{0.15cm}{\rm rad} \hspace{0.25cm} = \hspace{0.2cm} \phi_{\rm x1}+ \phi_{\rm x2}-\phi_{\rm o} \hspace{0.05cm} .$$
The corresponding magnitudes $|R_{\rm o}|$, $|R_{\rm x1}|$ and $|R_{\rm x1}|$ as well as the angles $\phi_{\rm o}$, $\phi_{\rm x1}$ and $\phi_{\rm x2}$ can be taken from the graph .
Please note:
- The exercise belongs to the chapter Laplace Transform and p-Transfer Function.
Questions
Solution
(1) The $p$–transfer function is:
]
- $$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$
- The conventional transfer function (the frequency response) is obtained via the substitution $p = {\rm j} \cdot 2 \pi f$:
- $$H(f)= K \cdot \frac {{\rm j \hspace{0.05cm}2\pi \it f} - p_{\rm o }} {({\rm j \hspace{0.05cm}2\pi \it f} - p_{\rm x 1})({\rm j \hspace{0.05cm}2\pi \it f} - p_{\rm x 2})} = {\rm e}^{-a(f)\hspace{0.05cm}}\cdot {\rm e}^{- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.05cm} .$$
- In the limiting case $f → \infty$ the following is obtained for the magnitude, attenuation and phase:
- $$\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} H(f)= \frac{K}{{\rm j \hspace{0.05cm}2\pi \it f}}\hspace{0.15cm}\Rightarrow \hspace{0.15cm}\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} |H(f)|\hspace{0.15cm}\underline {= 0} \hspace{0.05cm} \Rightarrow \hspace{0.15cm}\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} a(f)= \infty,\hspace{0.1cm} \lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} b(f)\underline {= {\pi}/{2}\hspace{0.1cm}(+90^\circ)} \hspace{0.01cm}.$$
(2) From the general equation in subtask (1) the following is obtained with the limit process $f → 0$:
$|H(f)|$, $a(f)$ and $b(f)$
- $$|H(f=0)|= -\frac {K \cdot p_{\rm o }} {p_{\rm x 1}\cdot p_{\rm x 2}} = \frac {5 \cdot 1}{ (-3 + 3{\rm j})\cdot (-3 + 3{\rm j})}= \frac {5 }{18}\hspace{0.15cm}\underline {\approx 0.278} \hspace{0.05cm} ,$$
- $$a(f=0)=- {\rm ln} \hspace{0.1cm}\hspace{0.15cm}\underline { |H(f=0)|= 1.281\,{\rm Np }} \hspace{0.05cm} .$$
The screen capture of the Flash–module "Causal Systems" summarizes the results of this exercise:
- middle axis (blue): magnitude $|H(f)|$,
- left axis (red): attenuation $a(f)$,
- right axis (green): phase $b(f)$.
- black point: values for $2\pi f = 4.$
Pole-zero diagram and some auxiliary quantities
(3) Entsprechend der detaillierten Beschreibung im Theorieteil gilt für die Dämpfungsfunktion:
- $$a(f)= -{\rm ln} \hspace{0.1cm} K + {\rm ln} \hspace{0.1cm} |R_{\rm x1}|+{\rm ln} \hspace{0.1cm} |R_{\rm x2}|- {\rm ln} \hspace{0.1cm} |R_{{\rm o} }|\hspace{0.05cm} .$$
- Zu berücksichtigen ist weiterhin die Zusatzeinheit "Neper" $\rm (Np)$.
- Gesucht ist die Dämpfung bei $f = 2/\pi$. Dazu setzen wir $p = {\rm j} \cdot 2 \pi f = 4$ und ermitteln folgende Abstände:
- $$R_{\rm o} = 1 - 4 \cdot {\rm j}, \hspace{0.2cm}|R_{\rm o}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{1^2 + 4^2}= 4.123, \hspace{1.15cm} {\rm ln} \hspace{0.1cm}|R_{\rm o}| \hspace{0.25cm} = \hspace{0.2cm}1.417\,{\rm Np }\hspace{0.05cm},$$
- $$R_{\rm x1} = -3 - 1 \cdot {\rm j}, \hspace{0.2cm}|R_{\rm x1}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{3^2 + 1^2}= 3.162,\hspace{0.5cm} {\rm ln} \hspace{0.1cm}|R_{\rm x1}| \hspace{0.25cm} = \hspace{0.2cm}1.151\,{\rm Np }\hspace{0.05cm},$$
- $$ R_{\rm x2} = -3 - 7 \cdot{\rm j}, \hspace{0.2cm}|R_{\rm x2}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{3^2 + 7^2}= 7.616,\hspace{0.5cm} {\rm ln} \hspace{0.1cm}|R_{\rm x2}| \hspace{0.25cm} = \hspace{0.2cm}2.030\,{\rm Np }\hspace{0.05cm}.$$
$$\Rightarrow \hspace{0.3cm}a(f = \frac{4}{2\pi})= -{\rm ln} \hspace{0.1cm} 5 + 1.151+ 2.030- 1.417\hspace{0.15cm}\underline{=0.155\,{\rm Np }} \hspace{0.05cm}.$$
Das entspricht $0.155\ {\rm Np} \cdot 8.686 \ {\rm dB/Np} \hspace{0.15cm} \underline{= 1.346 \ {\rm dB}}$.
(4) Nach der Beschreibung im Theorieteil gilt wegen $K > 0$ für die Phasenfunktion:
- $$b(f ={2}/\pi) = \phi_{\rm x1} + \phi_{\rm x2}-\phi_{\rm o}\hspace{0.05cm},$$
- $$\phi_{\rm x1} ={\rm arctan}\hspace{0.15cm}(1/3) = 18.4^\circ\hspace{0.05cm}, \hspace{0.2cm}\phi_{\rm x2} = {\rm arctan}\hspace{0.15cm}(7/3) = 66.8^\circ\hspace{0.05cm},$$
- $$ \phi_{\rm o} = {\rm arctan}\hspace{0.15cm}(-1/4) = 180^\circ - 76^\circ = 104^\circ \hspace{0.3cm} \Rightarrow \hspace{0.3cm}b(f ={2}/\pi) = 18.4^\circ + 66.8^\circ - 104^\circ \hspace{0.15cm} \underline{= -18.8^\circ} \hspace{0.05cm}.$$
