Aufgaben:Exercise 2.4Z: Low-pass Influence with Synchronous Demodulation

• Return to book

Signals for DSB–AM and synchronous demodulation

Let us consider the same communication system as in  Exercise 2.4.  But this time, we will assume perfect frequency and phase synchronization for the synchronous demodulator $\rm (SD)$ .

The source signal  $q(t)$, the transmission signal  $s(t)$  and the signal in the synchronous demodulator before the low-pass filter  $b(t)$  are given as follows:

$$q(t) = q_1(t) + q_2(t)\hspace{0.2cm}{\rm mit }$$

$$q_1(t) = 2\,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t)\hspace{0.05cm},$$

$$q_2(t) = 1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm},$$

$$s(t) = q(t) \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm},$$

$$b(t) = s(t) \cdot 2 \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$

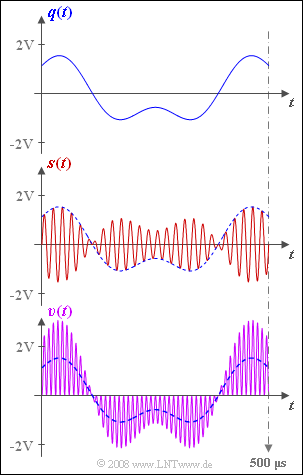
The graph shows the source signal  $q(t)$  at the top and the transmission signal  $s(t)$ in the middle.

The sink signal  $v(t)$  is shown at the bottom (violet waveform).

• This obviously does not match the source signal (blue dashed curve).
• The reason for this undesired result  $v(t) ≠ q(t)$  could be a missing or wrongly dimensioned low-pass filter, for example.

In the subtasks  (3)  and  (4) , a so-called  trapezoidal low-pass filter  is used, whose frequency response is as follows:

$$H_{\rm E}(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 -|f|}{f_2 -f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_1,} \\ {f_1 \le \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\hspace{0.94cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > f_2.} \\ \end{array}$$

Hints:

• This exercise belongs to the chapter   Synchronous Demodulation.
• Particular reference is made to the page   #Block diagram and time domain representation.
• In contrast to  Exercise 2.4 ,  $f_1$  and  $f_2$  do not describe signal frequencies, but instead relate to the low-pass filter.

Questions

1

Welche Aussagen sind über das Filter  $H_{\rm E}(f)$  möglich, das zur Gewinnung des auf der Angabenseite dargestellten Sinkensignals benutzt wurde?

	Die obere Grenzfrequenz ist zu hoch.
	Die obere Grenzfrequenz ist zu niedrig.
	Die untere Grenzfrequenz ist ungleich Null.

2

Mit welchen der nachfolgend aufgeführten Tiefpassfunktionen ist eine ideale Demodulation – das heißt  $v(t) = q(t)$  – prinzipiell möglich?

	Rechtecktiefpass,
	Gaußtiefpass,
	Trapeztiefpass,
	Spalttiefpass.

3

Wie ist die untere Eckfrequenz  $f_1$  eines Trapeztiefpasses mindestens zu wählen, damit keine Verzerrungen entstehen?

$f_{\text{1, min}} \ = \ $ $\ \text{kHz}$

4

Wie groß darf die obere Eckfrequenz  $f_2$  des Trapeztiefpasses höchstens sein, damit keine Verzerrungen entstehen?

$f_{\text{2, max}} \ = \ $ $\ \text{kHz}$

5

Welche Grenzfrequenz  $f_{\rm G}$  eines idealen, rechteckförmigen Tiefpasses würden Sie wählen, wenn Rauschstörungen nicht zu vernachlässigen sind?

	$f_{\rm G} = 4 \ \rm kHz$,
	$f_{\rm G} = 6 \ \rm kHz$,
	$f_{\rm G} = 10 \ \rm kHz$.

Musterlösung

Solution

(1)  Richtig ist die erste Aussage:

• Das dargestellte Sinkensignal  $v(t)$  stimmt exakt mit dem als Gleichung gegebenen Signal  $b(t)$  überein und enthält somit auch Anteile um die doppelte Trägerfrequenz.
• Das Filter  $H_{\rm E}(f)$  fehlt entweder ganz oder dessen obere Grenzfrequenz  $f_2$  ist zu hoch.
• Bezüglich der unteren Grenzfrequenz  $f_1$  ist nur die Aussage möglich, dass diese kleiner ist als die kleinste im Signal  $b(t)$  vorkommende Frequenz  $\text{(2 kHz)}$.
• Ob ein Gleichanteil durch das Filter entfernt wird oder nicht, ist unklar, da ein solcher im Signal  $b(t)$  nicht enthalten ist.

(2)  Richtig sind die Aussagen 1 und 3:

• Voraussetzung für eine verzerrungsfreie Demodulation ist, dass bis zu einer bestimmten Frequenz  $f_1$  alle Spektralanteile gleich und möglichst ungedämpft übertragen werden und alle Anteile bei Frequenzen  $f > f_2$  vollständig unterdrückt werden.
• Der Rechteck– und der Trapeztiefpass erfüllen diese Bedingung.

(3)  Sichergestellt werden muss, dass der  $\text{5 kHz}$–Anteil noch im Durchlassbereich liegt:

$$f_{\text{1, min}}\hspace{0.15cm}\underline{ =5 \ \rm kHz}.$$

(4)  Alle Spektralanteile in der Umgebung der doppelten Trägerfrequenz – genauer gesagt zwischen  $\text{95 kHz}$  und  $\text{ 105 kHz}$  – müssen vollständig unterdrückt werden:

$$f_{\text{2, max}}\hspace{0.15cm}\underline{ =95 \ \rm kHz}.$$

• Ansonsten würde es zu nichtlinearen Verzerrungen kommen.

(5)  Richtig ist der Lösungsvorschlag 2:

• Die Grenzfrequenz}  $f_{\rm G} = \text{ 4 kHz}$  hätte (lineare) Verzerrungen zur Folge, da dann der  $\text{5 kHz}$–Anteil abgeschnitten würde.
• Zu bevorzugen ist der Tiefpass mit der Grenzfrequenz  $f_{\rm G} = \text{6 kHz}$, da mit  $f_{\rm G} = \text{10 kHz}$  dem Nutzsignal $v(t)$ mehr Rauschanteile überlagert wären.