Difference between revisions of "Theory of Stochastic Signals/Probability Density Function (PDF)"
| Line 25: | Line 25: | ||
The first section "Probability Density Function" is organized as follows: | The first section "Probability Density Function" is organized as follows: | ||
| − | == | + | ==Properties of continuous random variables== |
| − | + | In the second chapter it was shown that the amplitude distribution of a discrete random variable is completely determined by its $M$ occurrence probabilities, where the step number $M$ usually has a finite value. | |
| − | + | Now we consider continuous (value) random variables. By this we mean random variables whose possible numerical values are uncountable ⇒ $M \to \infty$. | |
| − | + | Further it shall hold: | |
| − | * | + | *In the following we denote continuous random variables (mostly) with $x$ in contrast to the discrete random variables, which are denoted with $z$ as before. |
| − | * | + | *No statement is made here about a possible time discretization, i.e., continuous random variables can be discrete in time. |
| − | * | + | *Further, we assume for this chapter that there are no statistical bindings between the individual samples $x_ν$, or at least leave them out of consideration. |
{{Beispiel}} | {{Beispiel}} | ||
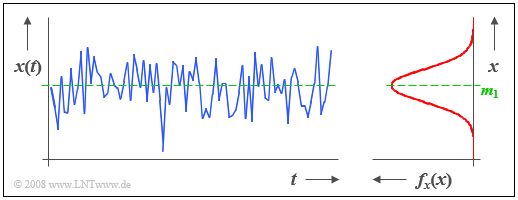
| − | + | The following image shows a section of a stochastic noise signal $x(t)$ whose instantaneous value can be taken as a continuous random variable $x$. | |
| − | [[File: P_ID41__Sto_T_3_1_S1_neu.png | + | [[File: P_ID41__Sto_T_3_1_S1_neu.png |center| Signal and PDF of a Gaussian noise signal]] |
| − | + | From the ''probability density function'' (PDF) shown on the right, it can be seen that instantaneous values around the mean $m_1$ occur most frequently for this example signal. Since there are no statistical bindings between the samples $x_ν$, such a signal is also referred to as '''white noise.''' | |
{{end}} | {{end}} | ||
| − | + | ||
==Definition der Wahrscheinlichkeitsdichtefunktion== | ==Definition der Wahrscheinlichkeitsdichtefunktion== | ||
Bei einer kontinuierlichen Zufallsgröße sind die Wahrscheinlichkeiten, dass diese ganz bestimmte Werte annimmt, identisch $0$. Deshalb muss zur Beschreibung einer kontinuierlichen Zufallsgröße stets auf die ''Wahrscheinlichkeitsdichtefunktion'' – abgekürzt WDF – übergegangen werden. | Bei einer kontinuierlichen Zufallsgröße sind die Wahrscheinlichkeiten, dass diese ganz bestimmte Werte annimmt, identisch $0$. Deshalb muss zur Beschreibung einer kontinuierlichen Zufallsgröße stets auf die ''Wahrscheinlichkeitsdichtefunktion'' – abgekürzt WDF – übergegangen werden. | ||
Revision as of 18:43, 24 December 2021
Contents
# OVERVIEW OF THE THIRD MAIN CHAPTER #
We consider here continuous random variables, i.e., random variables which can assume infinitely many different values, at least in certain ranges of values.
- Their applications in information and communication technology are manifold;
- They are used, among other things, for the simulation of noise signals and for the description of fading effects.
We restrict ourselves at first to the statistical description of the amplitude distribution. Inner statistical bindings of the underlying processes are considered only in the following main chapters 4 and 5.
In detail, the following are treated:
- the relationship between probability density function and cumulative distribution function;
- the calculation of expected values and moments;
- some special cases: uniform distribution, Gaussian distribution, exponential distribution, Laplace distribution, Rayleigh distribution, Rice distribution, Cauchy distribution;
- the generation of continuous random variables on a computer.
The first section "Probability Density Function" is organized as follows:
Properties of continuous random variables
In the second chapter it was shown that the amplitude distribution of a discrete random variable is completely determined by its $M$ occurrence probabilities, where the step number $M$ usually has a finite value.
Now we consider continuous (value) random variables. By this we mean random variables whose possible numerical values are uncountable ⇒ $M \to \infty$.
Further it shall hold:
- In the following we denote continuous random variables (mostly) with $x$ in contrast to the discrete random variables, which are denoted with $z$ as before.
- No statement is made here about a possible time discretization, i.e., continuous random variables can be discrete in time.
- Further, we assume for this chapter that there are no statistical bindings between the individual samples $x_ν$, or at least leave them out of consideration.
The following image shows a section of a stochastic noise signal $x(t)$ whose instantaneous value can be taken as a continuous random variable $x$.
From the probability density function (PDF) shown on the right, it can be seen that instantaneous values around the mean $m_1$ occur most frequently for this example signal. Since there are no statistical bindings between the samples $x_ν$, such a signal is also referred to as white noise.
Definition der Wahrscheinlichkeitsdichtefunktion
Bei einer kontinuierlichen Zufallsgröße sind die Wahrscheinlichkeiten, dass diese ganz bestimmte Werte annimmt, identisch $0$. Deshalb muss zur Beschreibung einer kontinuierlichen Zufallsgröße stets auf die Wahrscheinlichkeitsdichtefunktion – abgekürzt WDF – übergegangen werden.
Der Wert der Wahrscheinlichkeitsdichtefunktion $f_{x}(x)$ an der Stelle $x_\mu$ ist gleich der Wahrscheinlichkeit, dass der Momentanwert der Zufallsgröße $x$ in einem (unendlich kleinen) Intervall der Breite $Δx$ um $x_\mu$ liegt, dividiert durch $Δx$: $$f_x(x=x_\mu) = \lim_{\rm \Delta \it x \hspace{0.05cm}\to \hspace{0.05cm}\rm 0}\frac{\rm Pr \{\it x_\mu-\rm \Delta \it x/\rm 2 \le \it x \le x_\mu \rm +\rm \Delta \it x/\rm 2\}}{\rm \Delta \it x}.$$
Diese äußerst wichtige Beschreibungsgröße weist folgende Eigenschaften auf:
- Obwohl aus dem beispielhaften Zeitverlauf auf der letzten Seite zu ersehen ist, dass die häufigsten Signalanteile bei $x = m_1$ liegen und die Wahrscheinlichkeitsdichtefunktion hier ihren größten Wert besitzt, ist die Wahrscheinlichkeit ${\rm Pr}(x = m_1$), dass der Momentanwert exakt gleich dem Mittelwert $m_1$ ist, identisch $0$.
- Für die Wahrscheinlichkeit, dass die Zufallsgröße im Bereich zwischen $x_u$ und $x_o$ liegt, gilt:
- $${\rm Pr}(x_{\rm u} \le x \le x_{\rm o}) = \int_{x_{\rm u}}^{x_{\rm o}} f_{x}(x) \,{\rm d}x.$$
- Als wichtige Normierungseigenschaft ergibt sich daraus für die Fläche unter der WDF mit den Grenzübergängen $x_{\rm u} → \hspace{0.05cm} – \hspace{0.05cm} ∞$ und $x_{\rm o} → +∞:$
- $$\int_{-\infty}^{+\infty} f_{x}(x) \,{\rm d}x = \rm 1.$$
- Die entsprechende Gleichung für wertdiskrete, $M$-stufige Zufallsgrößen sagt aus, dass die Summe über die $M$ Auftrittswahrscheinlichkeiten den Wert $1$ ergibt.
Hinweis zur Nomenklatur: In der Fachliteratur wird meist zwischen der Zufallsgröße $X$ und deren Realisierungen $x ∈ X$ unterschieden. Samit lautet die obige Definitionsgleichung
$$f_{X}(X=x) = \lim_{{\rm \Delta} x \hspace{0.05cm}\to \hspace{0.05cm} 0}\frac{{\rm Pr} \{ x-{\rm \Delta} x/2 \le X \le x +{\rm \Delta} x/ 2\}}{{\rm \Delta} x}.$$
Wir haben in unserem Lerntutorial auf diese genauere Nomenklatur weitgehend verzichtet, um nicht für eine Größe zwei Buchstaben zu verbrauchen. Kleinbuchstaben (wie $x$) bezeichnen bei uns oft Signale und Großbuchstaben (wie $X$) die zugehörigen Spektren. Trotzdem müssen wir heute (2017) ehrlicher Weise zugeben, dass die Entscheidung von 2001 nicht ganz glücklich war.
WDF-Definition für diskrete Zufallsgrößen
Aus Gründen einer einheitlichen Darstellung aller Zufallsgrößen (sowohl wertdiskret als auch wertkontinuierlich) ist es zweckmäßig, die Wahrscheinlichkeitsdichtefunktion auch für diskrete Zufallsgrößen zu definieren. Wendet man die Definitionsgleichung der letzten Seite auf diskrete Zufallsgrößen an, so nimmt die WDF an einigen Stellen $x_\mu$ aufgrund des nicht verschwindend kleinen Wahrscheinlichkeitswertes und des Grenzübergangs $Δx → 0$ unendlich große Werte an. Somit ergibt sich für die WDF eine Summe von Diracfunktionen (bzw. Distributionen): $$f_{x}(x)=\sum_{\mu=1}^{M}p_\mu\cdot {\rm \delta}( x-x_\mu).$$
Die Gewichte dieser Diracfunktionen sind gleich den Wahrscheinlichkeiten $p_\mu = {\rm Pr}(x = x_\mu$).
Hier noch ein Hinweis, um die unterschiedlichen Beschreibungsgrößen für diskrete und kontinuierliche Zufallsgrößen einordnen zu können: Wahrscheinlichkeit und Wahrscheinlichkeitsdichtefunktion stehen in ähnlichem Verhältnis zueinander wie im Buch Signaldarstellung
- ein diskreter Spektralanteil einer harmonischen Schwingung ⇒ Linienspektrum, und
- ein kontinuierliches Spektrum eines energiebegrenzten (impulsförmigen) Signals.
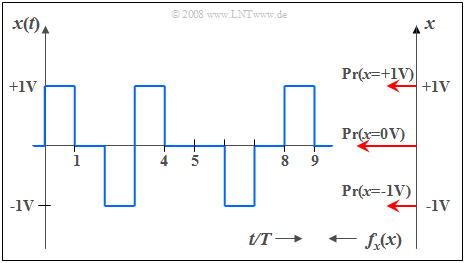
Nachfolgend sehen Sie einen Ausschnitt eines Rechtecksignals mit drei möglichen Werten, wobei der Signalwert $0 \ \rm V$ doppelt so häufig wie die äußeren Signalwerte ($\pm 1 \ \rm V$) auftritt.
Somit lautet die dazugehörige WDF (Anteile von oben nach unten): $$f_{x}(x) = 0.25 \cdot \delta(x-{\rm 1 \ V}) + 0.5\cdot \delta(x) + 0.25\cdot \delta (x + 1\ \rm V).$$
Zur Vertiefung der hier behandelten Thematik empfehlen wir das folgende Lernvideo:
Wahrscheinlichkeit und Wahrscheinlichkeitsdichtefunktion
Numerische Ermittlung der WDF
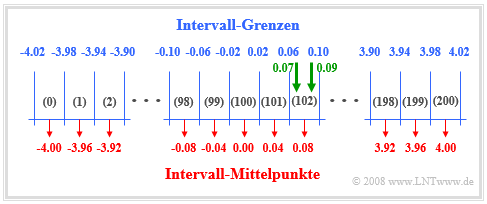
Sie sehen hier ein Schema zur numerischen Ermittlung der Wahrscheinlichkeitsdichtefunktion.
Setzt man voraus, dass die vorliegende Zufallsgröße $x$ außerhalb des Bereichs von $x_{\rm min} = –4.02$ bis $x_{\rm max} = +4.02$ nur vernachlässigbar kleine Anteile besitzt, so geht man folgendermaßen vor:
- Man teilt den Wertebereich von $x$ in $I$ Intervalle gleicher Breite $Δx$ ein und definiert ein Feld $\text{WDF}[0 : I–1]$. In obiger Skizze ist $I = 201$ und dementsprechend $Δx = 0.04$ gewählt.
- Die Zufallsgröße $x$ wird nun $N$ mal nacheinander aufgerufen und dabei jeweils geprüft, zu welchem Intervall $i_{\rm akt}$ die aktuelle Zufallsgröße $x_{\rm akt}$ gehört: $i_{\rm akt} = ({\rm int})((x + x_{\rm max})/Δx)$.
- Das entsprechende Feldelement WDF( $i_{\rm akt}$) wird dann um $1$ erhöht. Nach $N$ Durchläufen beinhaltet dann $\text{WDF}[i_{\rm akt}]$ die Anzahl der Zufallszahlen, die zum Intervall $i_{\rm akt}$ gehören.
- Die tatsächlichen WDF-Werte erhält man, wenn am Ende noch alle Feldelemente $\text{WDF}[i]$ mit $0 ≤ i ≤ I–1$ durch $N · Δx$ dividiert werden.
Aus den eingezeichneten grünen Pfeilen in obiger Grafik erkennt man:
- Der Wert $x_{\rm akt} = 0.07$ führt zum Ergebnis $i_{\rm akt} =$ (int) ((0.07 + 4.02)/0.04) = (int) $102.25$. Hierbei bedeutet (int) eine Integerwandlung nach der Float-Division ⇒ $i_{\rm akt} = 102$.
- Das gleiche Intervall $i_{\rm akt} = 102$ ergibt sich für $0.06 < x_{\rm akt} < 0.10$, zum Beispiel also auch für $x_{\rm akt} = 0.09$.
Aufgaben zum Kapitel
Aufgabe 3.1: cos² - und Dirac-WDF
Aufgabe 3.1Z: Dreieckförmige WDF