Difference between revisions of "Aufgaben:Exercise 4.7Z: Generation of a Joint PDF"
From LNTwww
m (Guenter moved page Exercise 4.7Z: Generation of a joint PDF to Exercise 4.7Z: Generation of a Joint PDF) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID423__Sto_Z_4_7.png|right|frame|Requirements for the generation of a <br> | + | [[File:P_ID423__Sto_Z_4_7.png|right|frame|Requirements for the generation of a <br>two-dimensional random variable]] |
| − | Given statistically independent quantities $u$ and $v$, both of which are uniformly distributed between $-1$ and $+1$ and thus each have variance $\sigma^2 = 2/3$ | + | Given statistically independent quantities $u$ and $v$, |
| + | *both of which are uniformly distributed between $-1$ and $+1$, and | ||
| + | *thus each have variance $\sigma^2 = 2/3$, | ||
| + | |||
| + | |||
| + | generate a two-dimensional random variable $(x,\hspace{0.08cm} y)$ where for the components: | ||
:$$x = A \cdot u + B \cdot v + C,$$ | :$$x = A \cdot u + B \cdot v + C,$$ | ||
:$$y= D \cdot u + E \cdot v + F.$$ | :$$y= D \cdot u + E \cdot v + F.$$ | ||
| − | The | + | The two-dimensional random variable $(x,\hspace{0.08cm} y)$ to be generated should have the following statistical properties: |
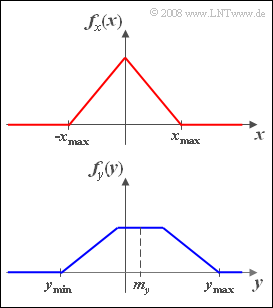
* Let the variances be $\sigma_x^2 = 4$ and $\sigma_y^2 = 10$. | * Let the variances be $\sigma_x^2 = 4$ and $\sigma_y^2 = 10$. | ||
* Let the random variable $x$ be mean-free $(m_x =0)$. | * Let the random variable $x$ be mean-free $(m_x =0)$. | ||
| − | * For the mean of $y$ let $m_y = 1$ hold. | + | * For the mean of $y$ let $m_y = 1$ hold. |
* The correlation coefficient between $x$ and $y$ is $\rho_{xy} = \sqrt{0.9} = 0.949.$ | * The correlation coefficient between $x$ and $y$ is $\rho_{xy} = \sqrt{0.9} = 0.949.$ | ||
* The random variable $x$ possess a triangular PDF $f_x(x)$ corresponding to the above graph. | * The random variable $x$ possess a triangular PDF $f_x(x)$ corresponding to the above graph. | ||
| Line 19: | Line 24: | ||
| − | + | Hints: | |
| − | |||
| − | |||
| − | |||
*The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Linear_Combinations_of_Random_Variables|Linear Combinations of Random Variables]]. | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Linear_Combinations_of_Random_Variables|Linear Combinations of Random Variables]]. | ||
| − | *In particular, reference is made to the page [Theory_of_Stochastic_Signals/Linear_Combinations_of_Random_Variables#Generation_of_correlated_random_variables|Generation of correlated random variables]]. | + | *In particular, reference is made to the page [[Theory_of_Stochastic_Signals/Linear_Combinations_of_Random_Variables#Generation_of_correlated_random_variables|Generation of correlated random variables]]. |
| − | *To avoid ambiguity, it is specified that all coefficients $A$, ... , $F$ should be non-negative. | + | *To avoid ambiguity, it is specified that all coefficients $A$, ... , $F$ should be non-negative. |
| Line 44: | Line 46: | ||
| − | {Determine the coefficients $D$ and $E$, where $D > E$ should hold. | + | {Determine the coefficients $D$ and $E$, where $D > E$ should hold. |
|type="{}"} | |type="{}"} | ||
$D \ = \ $ { 3.464 3% } | $D \ = \ $ { 3.464 3% } | ||
| Line 50: | Line 52: | ||
| − | {Specify the maximum values for $x$ and $y$ | + | {Specify the maximum values for $x$ and $y$. |
|type="{}"} | |type="{}"} | ||
$x_\text{max}\ = \ $ { 3.464 3% } | $x_\text{max}\ = \ $ { 3.464 3% } | ||
Revision as of 17:39, 25 February 2022
Given statistically independent quantities $u$ and $v$,
- both of which are uniformly distributed between $-1$ and $+1$, and
- thus each have variance $\sigma^2 = 2/3$,
generate a two-dimensional random variable $(x,\hspace{0.08cm} y)$ where for the components:
- $$x = A \cdot u + B \cdot v + C,$$
- $$y= D \cdot u + E \cdot v + F.$$
The two-dimensional random variable $(x,\hspace{0.08cm} y)$ to be generated should have the following statistical properties:
- Let the variances be $\sigma_x^2 = 4$ and $\sigma_y^2 = 10$.
- Let the random variable $x$ be mean-free $(m_x =0)$.
- For the mean of $y$ let $m_y = 1$ hold.
- The correlation coefficient between $x$ and $y$ is $\rho_{xy} = \sqrt{0.9} = 0.949.$
- The random variable $x$ possess a triangular PDF $f_x(x)$ corresponding to the above graph.
- The random variable $y$ has a trapezoidal PDF $f_y(y)$ according to the lower graph.
Hints:
- The exercise belongs to the chapter Linear Combinations of Random Variables.
- In particular, reference is made to the page Generation of correlated random variables.
- To avoid ambiguity, it is specified that all coefficients $A$, ... , $F$ should be non-negative.
Questions
Solution
(1) Given the mean values given, it must hold:
- $$ C = m_x\hspace{0.15cm}\underline{ = 0},$$
- $$ F = m_y\hspace{0.15cm}\underline{ = 1}.$$
(2) Taking into account $\sigma^2 = 2/3$ holds:
- $$\sigma_x^2 = \sigma^2 \cdot ( A^2 + B^2)= {2}/{3} \cdot ( A^2 + B^2) .$$
- Because $\sigma_x^2 = 4$ it follows $A^2 + B^2= 6$.
- A triangular PDF means that $A = \pm B$ must hold.
- Thus, since negative coefficients have been excluded, we obtain:
- $$ A = B = \sqrt{3}\hspace{0.15cm}\underline{ = 1.732}.$$
(3) With $ A = B = \sqrt{3}$ corresponding to the last subtask, two equations of determination remain for $D$ and $E$:
- $$\sigma_y^2 = \sigma^2 \cdot ( D^2 + E^2)= 10 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} D^2 + E^2 = \frac {\sigma_y^2}{\sigma^2} = \frac {10}{2/3} \stackrel{!}{=}15,$$
- $$\rho_{xy} = \frac{A \cdot D + B \cdot E}{\sqrt{(A^2 + B^2)(D^2 + E^2)}} = \frac{\sqrt{3} \cdot (D + E)}{\sqrt{6 \cdot (D^2 + E^2)}} \stackrel{!}{=} \sqrt{0.9}.$$
- From this it further follows: $D + E = \sqrt{1.8 \cdot ( D^2 + E^2)} = \sqrt{27} = 3 \cdot \sqrt{3}.$
- The equation, in conjunction with $D^2 + E^2 = 15$ and the constraint $(D>E)$ leads to the result:
- $$ D= 2 \cdot \sqrt{3}\hspace{0.15cm}\underline{ = 3.464}, \hspace{0.5cm}E= \sqrt{3} \hspace{0.15cm}\underline{= 1.732}.$$
(4) The random variables $x$ and $y$ respectively, take their maximum values when respectively $u= +1$ and $v= +1$ holds:
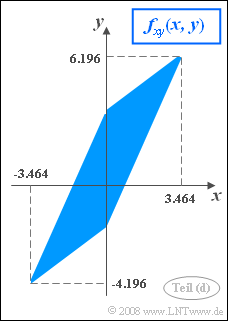
- $$ x_\text{max}= A+B \hspace{0.15cm}\underline{ = +3.464}, \hspace{0.5cm} x_\text{min} = - A - B= -3.464.$$
- $$ y_\text{max}= D+E+F \hspace{0.15cm}\underline{ = +6.196}, \hspace{0.5cm} y_\text{min} = -D-E+F= -4.196.$$