Aufgaben:Exercise 1.2Z: Bit Error Measurement

• Return to book

Simulated bit error frequencies

The bit error probability

$$p_{\rm B} = {1}/{2} \cdot{\rm erfc} \left( \sqrt{{E_{\rm B}}/{N_0}}\right)$$

of a binary system was simulatively determined by a measurement of the bit error rate  $\rm (BER)$:

$$h_{\rm B} = {n_{\rm B}}/{N}.$$

Often,  $h_{\rm B}$  is also called  "bit error frequency".

In above equations mean:

• $E_{\rm B}$:   energy per bit,
• $N_0$:   AWGN noise power density,
• $n_{\rm B}$:   number of bit errors occurred,
• $N$:     number of simulated bits of a test series.

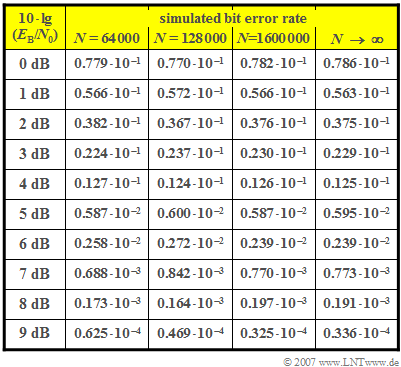
The table shows the results of some test series with  $N = 6.4 \cdot 10^4$,  $N = 1. 28 \cdot 10^5$  and  $N = 1.6 \cdot 10^6$. The last column named  $N \to \infty$  gives the bit error probability  $p_{\rm B}$. 

The following properties are referred to in the exercise questionnaire:

• The bit error frequency  $h_{\rm B}$  is  (to a first approximation)  a Gaussian distributed random variable with mean  $m_h = p_{\rm B}$  and variance  $\sigma_h^2 \approx p_{\rm B}/N$.
• The relative deviation of the bit error frequency from the probability is

$$\varepsilon_{\rm rel}= \frac {h_{\rm B}-p_{\rm B}}{p_{\rm B}}\hspace{0.05cm}.$$

• As a rough rule of thumb on the required accuracy,  the number of measured bit errors should be  $n_{\rm B} \ge 100$. 

Note:

• The exercise belongs to the chapter  "Error Probability for Baseband Transmission".

Questions

1

Which of the following statements are true?

	The accuracy of the BER measurement is independent of  $N$.
	The larger  $N$  is,  the more accurate the BER measurement is on average.
	The larger  $N$  is,  the more accurate each individual BER measurement is.

2

Give the standard deviation  $\sigma_h$  for different  $N$.  Let  $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$.

$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm} σ_h \ = \ $ $\ \cdot 10^{ -3 }\ $

$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} σ_h \ = \ $ $\ \cdot 10^{ -3 }\ $

3

What is the respective relative deviation for  $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$?

$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm} ε_{\rm rel} \ = \ $ $\ \%$

$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} ε_{\rm rel} \ = \ $ $\ \%$

4

Give the standard deviation  $\sigma_h$  for different  $N$.  Let $10 \cdot \lg \ E_{\rm B}/N_0 = 9 \ \rm dB$.

$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm} σ_h \ = \ $ $\ \cdot 10^{ -5 }\ $

$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} σ_h \ = \ $ $\ \cdot 10^{ -5 }\ $

5

What is the respective relative deviation for  $10 \cdot \lg \ E_{\rm B}/N_0 = 9 \ \rm dB$?

$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm} ε_{\rm rel} \ = \ $ $\ \%$

$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} ε_{\rm rel} \ = \ $ $\ \%$

6

Up to what (logarithmic)  $E_{\rm B}/N_0$  value is  $N = 1.6 \cdot 10^6$  sufficient due to the condition  $n_{\rm B} \ge 100$? 

$\text{Maximum} \ \big [10 \cdot \lg \ E_{\rm B}/N_0 \big] \ = \ $ $\ \rm dB$

Solution

Solution

(1)  Only the second solution is correct:

• Of course, the accuracy of the BER measurement is influenced by the parameter $N$ to a large extent. On statistical average, the BER measurement naturally becomes better when $N$ is increased.
• However, there is no deterministic relationship between the number of simulated bits and the accuracy of the BER measurement, as shown, for example, by the results for $10 \cdot \lg \ E_{\rm B}/N_0 = 6 \ \rm dB$:
• For $N = 6.4 \cdot 10^4\ (n_{\rm B} = 0.258 \cdot 10^{-2})$, the deviation from the true value $(0.239 \cdot 10^{-2})$ is smaller than for $N = 1.28 \cdot 10^5\ (n_{\rm B} = 0.272 \cdot 10^{-2})$.

(2)  At $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$, i.e. $E_{\rm B} = N_0$, the following values are obtained:

$$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.0786}{64000}}\hspace{0.1cm}\underline {\approx 1.1 \cdot10^{-3}}\hspace{0.05cm},$$

$$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} \sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.0786}{1600000}}\hspace{0.1cm}\underline {\approx 0.22 \cdot10^{-3}}\hspace{0.05cm}.$$

(3)  For this, $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$ yields the following values:

$$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}} = \frac{0.0779-0.0786}{0.0786}\hspace{0.1cm}\underline {\approx -0.9\% }\hspace{0.05cm}$$

$$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm} \varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}}= \frac{0.0782-0.0786}{0.0786}\hspace{0.1cm}\underline {\approx -0.5\% } \hspace{0.05cm}.$$

(4)  Due to the smaller error probability, the values are now smaller than in subtask (2):

$$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.336 \cdot 10^{-4}}{6.4 \cdot 10^{4}}}\hspace{0.1cm}\underline {\approx 2.3 \cdot 10^{-5}}\hspace{0.05cm},$$

$$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm}\sigma_h = \sqrt{{p}/{N}}= \sqrt{\frac{0.336 \cdot 10^{-4}}{1.6 \cdot 10^{6}}}\hspace{0.1cm}\underline {\approx 0.46 \cdot10^{-5}}\hspace{0.05cm}.$$

(5)  Despite the much smaller standard deviation $\sigma_h$, the smaller error probability results in larger relative deviations for $10 \cdot \lg \ E_{\rm B}/N_0 = 9 \ \rm dB$ than for $10 \cdot \lg \ E_{\rm B}/N_0 = 0 \ \rm dB$:

$$N = 6.4 \cdot 10^4\text{:}\hspace{0.4cm}\varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}}= \frac{0.625 \cdot 10^{-4} - 0.336 \cdot 10^{-4}}{0.336 \cdot 10^{-4}}\hspace{0.1cm}\underline { \approx 86\% } \hspace{0.05cm},$$

$$N = 1.6 \cdot 10^6\text{:}\hspace{0.4cm}\varepsilon_{\rm rel}= \frac{h_{\rm B}- p_{\rm B}}{h_{\rm B}}= \frac{0.325 \cdot 10^{-4} - 0.336 \cdot 10^{-4}}{0.336 \cdot 10^{-4}}\hspace{0.1cm}\underline {\approx -3.3\%}\hspace{0.05cm}.$$

(6)  The number of measured bit errors should be $n_{\rm B} \ge 100$. Therefore, approximately (rounding errors should be taken into account):

$$n_{\rm B} = {p_{\rm B}}\cdot {N} > 100 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm B} > \frac{100}{1.6 \cdot 10^6} = 0.625 \cdot 10^{-4}\hspace{0.05cm}.$$

• It further follows that in the simulation for $10 \cdot \lg \ E_{\rm B}/N_0\hspace{0.05cm}\underline{ = 8 \ \rm dB}$ still a sufficient number of bit errors occurred $(n_{\rm B} =315)$, while for $10 \cdot \lg \ E_{\rm B}/N_0 = 9 \ \rm dB$ on average only $n_{\rm B} =52$ errors are to be expected.
• For this dB value, about twice the number of bits would have to be simulated.