Aufgaben:Exercise 4.16Z: Multi-dimensional Data Reduction

• Return to book

Correlation matrices
$\mathbf{K_y}$  and  $\mathbf{K_z}$

We consider Gaussian zero mean random variables  $\mathbf{x}$,  $\mathbf{y}$  and  $\mathbf{z}$  with dimensions  $N= 1$,  $N= 2$  and  $N= 3$:

• The one-dimensional random variable  $\mathbf{x}$  is characterized by the variance  $\sigma^2 = 1$  and the standard deviation   $\sigma = 1$  respectively.
  Because of the dimension  $N= 1$  $\mathbf{x} = x$ holds.

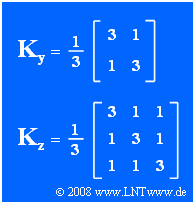
• The correlation coefficient between the components  $y_1$  and  $y_2$  of the 2D random variable  $\mathbf{y}$  is  $\rho = 1/3$  $($see matrix  $\mathbf{K_y})$.
  $y_1$ and $y_2$ also have the standard deviation $\sigma = 1$.

• The statistics of the three-dimensional random variable  $\mathbf{z}$  is completely determined by the correlation matrix  $\mathbf{K_z}$ .

If one quantizes the random variable  $\mathbf{x}$  in the range between  $-4$  and  $+4$  with interval width  $\Delta_x = 1/32$, there are altogether  $N_1 = 256$  different quantization values, for whose transmission thus  $n_1 = 8\ \rm {bit}$  would be needed.

Similarly, the random variable  $\mathbf{y}$  results in a total of  $N_2 = 256^2 = 65536$  different quantized value pairs, if the correlation between  $y_1$  and  $y_2$  is not taken into account.

Exploiting this correlation– for example, by coordinate transformation from the original system  $(y_1, y_2)$  to the new system  $(\eta_1, \eta_2)$  – results in a smaller number  $N_2\hspace{0.01cm}'$  of quantized value pairs.

• Here, it is to be considered that each component is to be quantized according to its respective dispersion  $(\sigma_1$  resp.  $\sigma_2)$  in the range of  $-4$  to  $+4$  and the quantization intervals should be the same in both directions:   $\Delta_x = \Delta_y =1/32$.

• We denote the quotient  $N_2\hspace{0.01cm}'/N_2$  as the data reduction factor with respect to the 2D random variable  $\mathbf{y}$.
• In analogous definition  $N_3'/N_3$  is the corresponding reduction factor of the 3D random variable  $\mathbf{z}$  for  $\Delta_x = \Delta_y =\Delta_z =1/32.$
• Note that in both cases the smallest possible value of this quotient would be favorable.

Hints:

• The exercise belongs to the chapter  Generalization to N-Dimensional Random Variables.
• In particular, reference is made to the page  Eigenvalues and Eigenvectors .
• Some basics on the application of vectors and matrices can be found on the pages  Determinant of a Matrix  and  Inverse of a Matrix .

• The equation of determination of the eigenvalues of  $\mathbf{K_z}$  is:   $\lambda^3 - 3 \lambda^2 + {24}/{9}\lambda - {20}/{27} = 0.$
• One of the three solutions of this equation is  $\lambda_1 = 5/3$.

Questions

1

Calculate the eigenvalues of the correlation matrix  $\mathbf{K_y}$. Let  $\lambda_1 \ge \lambda_2$ hold.

$\lambda_1 \ = \ $ $\ (\lambda_1 \ge \lambda_2)$

$\lambda_2 \ = \ $ $\ (\lambda_2 \le \lambda_1)$

2

What is the data reduction factor for the 2D random variable  $\mathbf{y}$?

$N_2\hspace{0.01cm}'/N_2 \ = $

3

It holds  $\lambda_1 = 5/3$.  Calculate the eigenvalues  $\lambda_2$  and  $\lambda_3 \le \lambda_2$  of  $\mathbf{K_z}$.

$\lambda_2 \ = \ $ $\ (\lambda_2 \ge \lambda_3)$

$\lambda_3 \ = \ $ $\ (\lambda_3 \le \lambda_2)$

4

What is the data reduction factor for the 3D random variable  $\mathbf{z}$?

$N_3\hspace{0.01cm}'/N_3 \ = $

Solution

Solution

(1)  From the condition  $\mathbf{K_y} - \lambda \cdot\mathbf{E} = 0$  follows:

$${\rm det}\left[ \begin{array}{cc} 1- \lambda & 1/3 \ 1/3 & 1- \lambda \end{array} \right] = (1-\lambda)^2 -{1}/{9} = 0 \hspace{0.3cm}\rightarrow \hspace{0.3cm}\lambda^2 -2\lambda+ {8}/{9}= 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\lambda_{1/2}= 1 \pm \sqrt{1-{8}/{9}}= 1 \pm {1}/{3}.$$

• The eigenvalues of this  $2\times2$ matrix are thus  $\lambda_1 = 4/3\hspace{0.15cm}\underline{=1.333}$  and  $\lambda_2 = 2/3\hspace{0.15cm}\underline{=0.667}$.

(2)  Without considering correlations, there are  $N_2 = \left({8}/{ \Delta_x}\right)^2= 256^2 = 65536$  different pairs of values.

• Taking into account the correlations and the fact that the two components created by coordinate rotation  $\eta_1$  and  $\eta_2$  are each in the range  $-4\sigma_1$  to  $+4\sigma_1$  $($bzw. from  $-4\sigma_2$  to  $+4\sigma_2)$ ) are to be quantized, one obtains

$$N_2\hspace{0.01cm}' = \frac{8 \hspace{0.05cm}\sigma_1}{\it \Delta_x}\cdot\frac{8 \hspace{0.05cm}\sigma_2}{\it \Delta_y}= N_2 \cdot \sigma_1 \cdot \sigma_2 .$$

• The quotient is thus with  $\sigma_1^2 = \lambda_1$  and  $\sigma_2^2 = \lambda_2$:

$${N_2\hspace{0.01cm}'}/{N_2} = \sigma_1 \cdot \sigma_2 = \sqrt{{4}/{3}} \cdot \sqrt{{2}/{3}} = \frac{2 \cdot \sqrt{2}}{3} \hspace{0.15cm}\underline{ \approx 0.943}.$$

(3)  The equation of determination of the eigenvalues of  $\mathbf{K_z}$  is:

$${\rm det} \left[ \begin{array}{ccc} 1-\lambda & 1/3 & 1/3\\ 1/3 & 1-\lambda & 1/3\\ 1/3 & 1/3 & 1-\lambda \end{array}\right] = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}(1- \lambda) \left[(1- \lambda)^2 - \frac{1}{9} \right]- \frac{1}{3} \left[\frac{1}{3}(1- \lambda) - \frac{1}{9} \right] + \frac{1}{3} \left[\frac{1}{9} - \frac{1}{3}(1- \lambda) \right] = 0$$

$$\Rightarrow \hspace{0.3cm}(1- \lambda) (\lambda^2 -2\lambda+ \frac{8}{9})- \frac{1}{9} (\frac{2}{3}- \lambda )+ \frac{1}{9} ( \lambda - \frac{2}{3})= 0$$

$$\Rightarrow \hspace{0.3cm}\lambda^2 - 2\lambda + \frac{8}{9} - \lambda^3 + 2 \lambda^2 - \frac{8}{9}\lambda - \frac{4}{27} + \frac{2}{9}\lambda = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\lambda^3 - 3 \lambda^2 + \frac{24}{9}\lambda - \frac{20}{27} = 0.$$

• This equation has already been given as a solution hint, as well as one of the solutions:   $\lambda_1= 5/3$.
• This gives the equation of determination for the further eigenvalues  $\lambda_2$  and  $\lambda_3$  to.

$$\frac{\lambda^3 - 3 \lambda^2 + {24}/{9}\lambda - {20}/{27}}{\lambda -{5}/{3}} = \lambda^2 - {4}/{3} \cdot \lambda + {4}/{9} =0.$$

• This equation of determination can be transformed as follows:   $(\lambda - {2}/{3})^2 =0.$

• The other eigenvalues besides  $\lambda_1= 5/3$  are thus equal and result in   $\lambda_2 = \lambda_3 =2/3\hspace{0.15cm}\underline{=0.667}$.

(4)  Analogous to the procedure in the subtask  (2)  results here:

$${N_3\hspace{0.01cm}'}/{N_3} = \sqrt{\lambda_1 \cdot \lambda_2\cdot \lambda_3} = \sqrt{\frac{5}{3} \cdot \frac{2}{3}\cdot \frac{2}{3}} = \sqrt{\frac{20}{27}} \hspace{0.15cm}\underline{ \approx 0.861}.$$