Difference between revisions of "Modulation Methods/Quadrature Amplitude Modulation"
m |
m |
||
| Line 62: | Line 62: | ||
:$$E_{\rm S} = \frac{{\rm E}[\hspace{0.05cm}|a_{\nu} |^2\hspace{0.05cm}]}{2}\cdot \int_{-\infty}^{+\infty} |g_s(t)|^2\,{\rm d} t = \frac{{\rm E}[|a_{\nu} |^2]}{2}\cdot \int_{-\infty}^{+\infty} |G_s(f)|^2\,{\rm d} f \hspace{0.05cm}.$$ | :$$E_{\rm S} = \frac{{\rm E}[\hspace{0.05cm}|a_{\nu} |^2\hspace{0.05cm}]}{2}\cdot \int_{-\infty}^{+\infty} |g_s(t)|^2\,{\rm d} t = \frac{{\rm E}[|a_{\nu} |^2]}{2}\cdot \int_{-\infty}^{+\infty} |G_s(f)|^2\,{\rm d} f \hspace{0.05cm}.$$ | ||
| − | + | On the other hand, $E_{\rm B} = E_{\rm S}/b$ gives the '''energy per bit''' when each binary symbol $b$ is combined to form the complex coefficient $a_\nu$ according to the signal space allocation. | |
| − | [[File:P_ID1710__Mod_T_4_3_S3a.png |right|frame| | + | [[File:P_ID1710__Mod_T_4_3_S3a.png |right|frame| Allocation for $\text{16-QAM}$]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ the top graph shows the signal space allocationfor $\text{16-QAM}$, where both the real and imaginary parts of the complex amplitude coefficients $a_ν$ can take one of four values $±1$ as well as $±1/3$ , respectively. |
| − | + | Averaging over the $16$ squared distances to the origin yields: | |
:$${\rm E}\big[\hspace{0.05cm} \vert a_{\nu}\vert^2 \hspace{0.05cm}\big] \hspace{0.18cm} = \hspace{0.18cm} \frac{4}{16} \cdot (1^2 + 1^2)+ \frac{4}{16} \cdot \left[(1/3 )^2 +(1/3)^2 \right ] | :$${\rm E}\big[\hspace{0.05cm} \vert a_{\nu}\vert^2 \hspace{0.05cm}\big] \hspace{0.18cm} = \hspace{0.18cm} \frac{4}{16} \cdot (1^2 + 1^2)+ \frac{4}{16} \cdot \left[(1/3 )^2 +(1/3)^2 \right ] | ||
+ \frac{8}{16} \cdot \left [1^2 + (1/3)^2\right ] $$ | + \frac{8}{16} \cdot \left [1^2 + (1/3)^2\right ] $$ | ||
:$$\Rightarrow \hspace{0.3cm}{\rm E}\big[\hspace{0.05cm} \vert a_{\nu}\vert^2 \hspace{0.05cm}\big] = {10}/{9}\approx 1.11 \hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm}{\rm E}\big[\hspace{0.05cm} \vert a_{\nu}\vert^2 \hspace{0.05cm}\big] = {10}/{9}\approx 1.11 \hspace{0.05cm}.$$ | ||
| − | + | In this order, the summands belong to | |
| − | * | + | *the four red, |
| − | * | + | *the four black, and |
| − | * | + | *the eight blue dots. |
Revision as of 15:53, 18 March 2022
Contents
- 1 General description and signal space allocation
- 2 System description using the equivalent low-pass signal
- 3 Power and energy of QAM Signals
- 4 Signalverläufe der 4–QAM
- 5 Fehlerwahrscheinlichkeit der 4–QAM
- 6 Quadratische QAM–Signalraumkonstellationen
- 7 Other signal space constellations
- 8 Nyquist– und Wurzel–Nyquist–QAM–Systeme
- 9 Offset–Quadraturamplitudenmodulation
- 10 Aufgaben zum Kapitel
- 11 Quellenverzeichnis
General description and signal space allocation
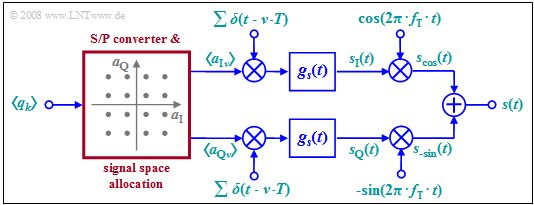
Due to the orthogonality of cosine and (minus) sine, two data streams can be transmitted independently via the same transmission channel. The diagram shows the general circuit schematic.
This very general model can be described as follows:
- The binary source symbol sequence $〈q_k〉$ with bit rate $R_{\rm B}$ is applied to the input. Thus, the time interval between two symbols is $T_{\rm B} = 1/R_{\rm B}$.
- Two multilevel amplitude coefficients $a_{{\rm I}ν}$ and $a_{{\rm Q}ν}$ are derived from each $b$ binary input symbols $q_k$ , where $\rm I$ stands for inphase and $\rm Q$ stands for quadrature component.
- If $b$ is even and the signal space allocation is quadratic, then the coefficients $a_{{\rm I}ν}$ and $a_{{\rm Q}ν}$ can each take on one of the $M = 2^{b/2}$ amplitude values with equal probability. This is then referred to as quadrature amplitude modulation $\rm (QAM)$.
- The example considered in the graph is for $\text{16-QAM}$ with $b = M = 4$ and correspondingly $M^2 =16$ signal space points. For a $\text{256-QAM}$ , $b = 8$ and $M = 16$ would apply: $2^b = M^2 = 256$.
- Next, the coefficients $a_{{\rm I}ν}$ and $a_{{\rm Q}ν}$ are each applied to a Dirac impulse as pulse weights. Thus, after shaping a pulse with the fundamental transmission pulse $g_s(t)$ , the following holds for both branches of the circuit diagram:
- $$s_{\rm I}(t) = \sum_{\nu = - \infty}^{+\infty}a_{\rm I\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm},\hspace{1cm}s_{\rm Q}(t) = \sum_{\nu = - \infty}^{+\infty}a_{\rm Q\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm}.$$
- Note that because of the redundancy-free conversion, the symbol duration $T$ of these signals is larger by a factor of $b$ than the bit duration $T_{\rm B}$ of the binary source signal. In the illustrated example $\text{(16-QAM)}$ , $T = 4 · T_{\rm B}$ holds.
- The QAM transmitted signal $s(t)$ is then the sum of the two signals multiplied by cosine and minus-sine, respectively:
- $$s_{\rm cos}(t) = s_{\rm I}(t) \cdot \cos(2 \pi f_{\rm T} t), \hspace{1cm} s_{\rm -sin}(t) = -s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t)$$
- $$\Rightarrow \hspace{0.3cm}s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) = s_{\rm I}(t) \cdot \cos(2 \pi f_{\rm T} t) - s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t) \hspace{0.05cm}.$$
$\text{Conclusion:}$ these statements can be summarized as follows:
- The two transmission branches $\rm (I,\ Q)$ can be thought of as two completely separate $M$-step ASK systems that do not interfere with each other as long as all components are optimally designed.
- Quadrature amplitude modulation thus makes it (ideally) possible to double the data rate while maintaining the same quality.
System description using the equivalent low-pass signal
Since the multiplication of $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ , with a cosine and minus-sine oscillation respectively, only causes a shift in the frequency domain and such a shift is a linear operation, the system description can be greatly simplified using the equivalent low-pass signals.
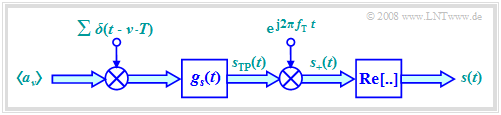
- The graph shows the simplified model in the baseband. This is equivalent to the block diagram considered so far.
- The serial-parallel conversion and the signal space allocation drawn in red in the block diagram are retained. This block is no longer drawn here.
- We also initially disregard the bandpass $H_{\rm BP}(f)$ , which is often introduced for technical reasons.
Please note the following:
- All double arrows in the baseband model denote complex quantities. The operations associated with them should also be understood as complex. For example, the complex amplitude coefficient $a_ν$  combines one inphase and one quadrature coefficient:
- $$a_\nu = a_{\rm I\hspace{0.03cm}\it \nu} + {\rm j} \cdot a_{\rm Q\hspace{0.03cm}\it \nu} \hspace{0.05cm}.$$
- The equivalent low-pass representation of the actual, physical and thus per se real transmitted signal $s(t)$ is always complex in QAM and with the partial signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ it holds that:
- $$s_{\rm TP}(t) = s_{\rm I}(t) + {\rm j} \cdot s_{\rm Q}(t) = \sum_{\nu = - \infty}^{+\infty} a_\nu \cdot g_s (t - \nu \cdot T)\hspace{0.05cm}.$$
- The analytical signal $s_+(t)$ is obtained from $s_{\rm TP}(t)$ by multiplying by the complex exponential function. The physical transmitted signal $s(t)$ ) is then obtained as the real part of $s_+(t)$.
- In order for the signs in the block diagram on the previous page and the sketched baseband model to match, multiplication by the negative sine wave is required in the quadrature branch, as shown in the following calculation:
- $$s(t) = {\rm Re}[s_{\rm +}(t)] = {\rm Re}[s_{\rm TP}(t) \cdot{\rm e}^{{\rm j}2\pi f_{\rm T} t}] $$
- $$\Rightarrow \hspace{0.3cm} s(t) = {\rm Re} \left[\left ( \sum (a_{\rm I\hspace{0.03cm}\it \nu} + {\rm j} \cdot a_{\rm Q\hspace{0.03cm}\it \nu} ) \cdot g_s (t - \nu \cdot T)\right )\left ( \cos(2 \pi f_{\rm T} t) + {\rm j} \cdot \sin(2 \pi f_{\rm T} t) \right )\right]= s_{\rm I}(t) \cdot \cos(2\pi f_{\rm T} t) - s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t) \hspace{0.05cm}.$$
- The influence of the bandpass $H_{\rm BP}(f)$, which in practice often has to be considered at the output of the QAM modulator, can be assigned to the pulse shape filter $g_s(t)$ . If the passband of the bandpass filter is symmetric about $f_{\rm T}$, its low-pass equivalent (in the time domain) $h_{\rm BP→TP}(t)$ is purely real and one can replace $g_s(t)$ with $g_s(t) \star h_{\rm BP→TP}(t)$ in the model.
Power and energy of QAM Signals
As shown in the chapter Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion in the book "Signal Representation", the power of the transmitted QAM signal $s(t)$ can also be calculated from the equivalent low-pass signal $s_{\rm TP}(t)$ , which is always complex. Thus, it is equally valid to write:
- $$P = \lim_{T_{\rm M} \rightarrow \infty} \frac{\rm 1}{T_{\rm M}}\cdot \int_{-T_{\rm M}/2}^{+T_{\rm M}/2} s^2(t)\,{\rm d} t = {\rm 1}/{2} \cdot \lim_{T_{\rm M} \rightarrow \infty} \frac{\rm 1}{T_{\rm M}}\cdot \int_{-T_{\rm M}/2}^{+T_{\rm M}/2} |s_{\rm TP}(t)|^2\,{\rm d} t \hspace{0.05cm}.$$
In contrast, the energy of the unbounded signals $s(t)$ and $s_{\rm TP}(t)$ is infinite.
However, if we restrict ourselves to a symbol duration $T$, we obtain the energy per symbol:
- $$E_{\rm S} = \frac{{\rm E}[\hspace{0.05cm}|a_{\nu} |^2\hspace{0.05cm}]}{2}\cdot \int_{-\infty}^{+\infty} |g_s(t)|^2\,{\rm d} t = \frac{{\rm E}[|a_{\nu} |^2]}{2}\cdot \int_{-\infty}^{+\infty} |G_s(f)|^2\,{\rm d} f \hspace{0.05cm}.$$
On the other hand, $E_{\rm B} = E_{\rm S}/b$ gives the energy per bit when each binary symbol $b$ is combined to form the complex coefficient $a_\nu$ according to the signal space allocation.
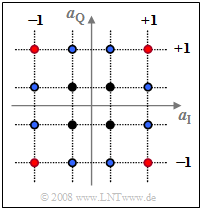
$\text{Example 1:}$ the top graph shows the signal space allocationfor $\text{16-QAM}$, where both the real and imaginary parts of the complex amplitude coefficients $a_ν$ can take one of four values $±1$ as well as $±1/3$ , respectively.
Averaging over the $16$ squared distances to the origin yields:
- $${\rm E}\big[\hspace{0.05cm} \vert a_{\nu}\vert^2 \hspace{0.05cm}\big] \hspace{0.18cm} = \hspace{0.18cm} \frac{4}{16} \cdot (1^2 + 1^2)+ \frac{4}{16} \cdot \left[(1/3 )^2 +(1/3)^2 \right ] + \frac{8}{16} \cdot \left [1^2 + (1/3)^2\right ] $$
- $$\Rightarrow \hspace{0.3cm}{\rm E}\big[\hspace{0.05cm} \vert a_{\nu}\vert^2 \hspace{0.05cm}\big] = {10}/{9}\approx 1.11 \hspace{0.05cm}.$$
In this order, the summands belong to
- the four red,
- the four black, and
- the eight blue dots.
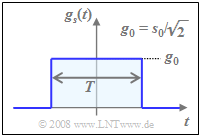
Bei NRZ–rechteckförmigem Sendegrundimpuls $g_s(t)$ mit der Amplitude $g_0$ und der Symboldauer $T$ ist das Spektrum $G_s(f)$ $\rm si$–förmig.
In diesem Fall gilt für
- die mittlere Energie pro Symbol:
- $$E_{\rm S} = 1/2 \cdot {\rm E}\big[\hspace{0.05cm}\vert a_{\nu} \vert ^2 \big]\hspace{0.05cm}\cdot g_0^2 \cdot T = {5}/{9}\cdot g_0^2 \cdot T \hspace{0.05cm}\approx 0.555 \cdot g_0^2 \cdot T \hspace{0.05cm},$$
- die mittlere Energie pro Bit:
- $$E_{\rm B} ={E_{\rm S} }/{4}= {5}/{36}\cdot g_0^2 \cdot T \approx 0.139 \cdot g_0^2 \cdot T \hspace{0.05cm}.$$
Die "maximale Hüllkurve" $s_0$ des Sendesignals $s(t)$ ist um den Faktor $\sqrt{2}$ größer als die Amplitude $g_0$ des Rechteckimpulses (siehe untere Skizze) und tritt bei einem der vier roten Amplitudenkoeffizienten auf, also immer dann, wenn $\vert a_{\rm I \it ν}\vert = \vert a_{\rm Q \it ν}\vert =1$ ist.
Signalverläufe der 4–QAM
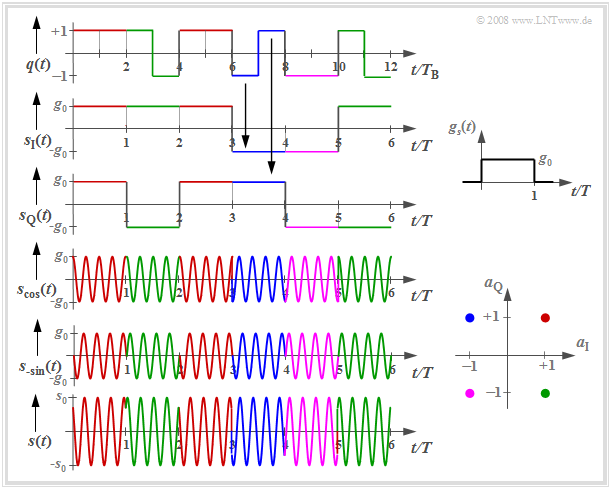
Die folgende Grafik zeigt die Signalverläufe der $\rm 4-QAM$, wobei die Farbgebung mit der oben definierten Signalraumzuordnung übereinstimmt.
Man erkennt aus diesen Darstellungen:
- die Seriell–Parallel–Wandlung des Quellensignals $q(t)$ in die beiden Komponentensignale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$, jeweils mit der Symboldauer $T = 2T_{\rm B}$ und den Signalwerten $±g_0$. Hierbei bezeichnet $T_{\rm B}$ die Bitdauer;
- die beiden trägerfrequenzmodulierten Signale $s_{\rm cos}(t)$ und $s_{\rm –sin}(t)$ mit Phasensprüngen um $±π$:
- $$s_{\rm cos} (t) = s_{\rm I} (t) \cdot \cos(2\pi f_{\rm T}t)\hspace{0.05cm},$$
- $$s_{\rm -sin} (t) = -s_{\rm Q} (t) \cdot \sin(2\pi f_{\rm T}t)\hspace{0.05cm}, $$
- das Sendesignal $s(t) = s_{\rm cos}(t) \ – \ s_{\rm –sin}(t)$ mit Phasensprüngen um Vielfache von $±π/2$; deren Hüllkurve ist gegenüber den beiden Komponentensignalen um den Faktor $\sqrt{2}$ größer:
- $$s_0 = \sqrt{2} \cdot g_0 \hspace{0.05cm}.$$
- Der Sendegrundimpuls $g_s(t)$ ist hier zur Vereinfachung der Darstellung zwischen $0$ bis $T$ als rechteckförmig angenommen, also unsymmetrisch bezüglich $t = 0$.
- Die zugehörige Spektralfunktion $G_s(f)$ dieses kausalen Impulses $g_s(t)$ ist komplex, was jedoch in diesem Zusammenhang keine Auswirkungen hat.
Fehlerwahrscheinlichkeit der 4–QAM
Im früheren Abschnitt Fehlerwahrscheinlichkeiten – ein kurzer Überblick wurde unter anderem die Bitfehlerwahrscheinlichkeit der binären Phasenmodulation $($englisch: Binary Phase Shift Keying, $\rm BPSK)$ angegeben. Nun werden die Ergebnisse auf die $\text{4-QAM}$ übertragen, wobei weiterhin folgende Voraussetzungen gelten:
- ein Sendesignal mit der mittleren Energie $E_{\rm B}$ pro Bit,
- AWGN–Rauschen mit der (einseitigen) Rauschleistungsdichte $N_0$,
- bestmögliche Empfängerrealisierung nach dem Matched–Filter–Prinzip.
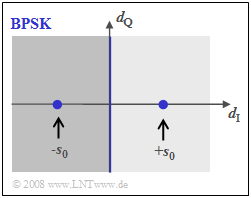
Die obere Abbildung zeigt das BPSK–Phasendiagramm des Detektionssignals $d(t)$, also inklusive dem Matched–Filter. Der Abstand des Nutzsignals von der Schwelle ($d_{\rm Q}$–Achse) beträgt zu den Detektionszeitpunkten jeweils $s_0$.
Mit den weiteren Gleichungen
- $$p_{\rm B} = {\rm Q}\left ( {s_0}/{\sigma_d } \right ), \hspace{0.2cm} E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}/{T_{\rm B} }$$
erhält man für die BPSK–Fehlerwahrscheinlichkeit: $$p_{\rm B, \hspace{0.1cm}BPSK} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$
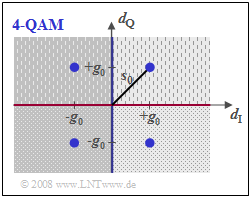
Bei der $\text{4-QAM}$ entsprechend der unteren Abbildung
- gibt es zwei Schwellen zwischen den Bereichen mit hellerem/dunklerem Hintergrund (blaue Linie) sowie zwischen den gepunkteten/gestrichelten Flächen (rote Linie),
- ist der Abstand von den Schwellen jeweils nur noch $g_0$ anstelle von $s_0$,
- ist aber die Rauschleistung $\sigma_d^2$ wegen der halben Symbolrate in jedem Teilzweig gegenüber der BPSK auch nur halb so groß.
Man erhält somit für die 4–QAM–Fehlerwahrscheinlichkeit mit den Gleichungen
- $$p_{\rm B} = {\rm Q}\left ( {g_0}/{\sigma_d } \right ), \hspace{0.2cm}g_{0} = {s_0}/{\sqrt{2}}, \hspace{0.2cm}E_{\rm B} = {1}/{2} \cdot s_0^2 \cdot T_{\rm B} ,\hspace{0.2cm} \sigma_d^2 = {N_0}(2 \cdot T_{\rm B} )$$
genau das gleiche Ergebnis wie für die BPSK:
- $$p_{\rm B, \hspace{0.1cm}4-QAM} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$
$\text{Fazit:}$
- Die $\text{4-QAM}$ hat bei idealen Bedingungen die gleiche Fehlerwahrscheinlichkeit wie die $\text{BPSK}$, obwohl die doppelte Informationsmenge übertragen werden kann.
- Sind allerdings die Bedingungen nicht mehr ideal – zum Beispiel bei einem ungewollten Phasenversatz zwischen Sender und Empfänger – so gibt es bei der 4–QAM eine deutlich stärkere Degradation als bei der BPSK.
- Dieser Fall wird im Abschnitt Fehlerwahrscheinlichkeit bei 4–QAM und BPSK des Buches „Digitalsignalübertragung” noch genauer betrachtet.
Quadratische QAM–Signalraumkonstellationen
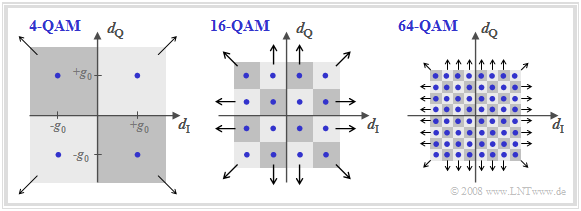
Die folgende Grafik zeigt die Signalraumkonstellationen von $\text{4-QAM}$, $\text{16-QAM}$ und $\text{64-QAM}$.
- Mit den hier gewählten Achsenbeschriftungen beschreiben die Bilder auch das Detektionsnutzsignal (zu den Detektionszeitpunkten) im äquivalenten Tiefpassbereich.
- Ebenfalls eingezeichnet sind die verschiedenen Entscheidungsgebiete, die dem verrauschten Detektionssignal zugeordnet werden.
- Die Pfeile geben an, wenn Entscheidungsgebiete bis ins Unendliche ausgedehnt sind.
Die Bilder beziehen sich nur auf die Detektionszeitpunkte und gelten für alle Nyquistsysteme
- wie die Rechteck–Rechteck–Konfiguration (Sendegrundimpuls und Empfangsfilter–Impulsantwort seien rechteckförmig)
- oder ein Wurzel–Cosinus–Rolloff–Nyquistsystem.
Die hier nicht dargestellten Übergänge zwischen den einzelnen Punkten (außerhalb der Detektionszeitpunkte) hängen aber sehr wohl vom gewählten Nyquistsystem ab.
Weiter ist zu diesen Darstellungen anzumerken:
- Bei echter QAM–Struktur – das heißt: die Signalraumkonstellation ist quadratisch oder zumindest rechteckförmig – lässt sich die „zweidimensionale” Detektion durch zwei „eindimensionale” Detektionsvorgänge vereinfacht lösen.
- Die $\text{16-QAM}$ ist somit nichts anderes als die parallele Übertragung zweier Digitalsignale mit jeweils $M = 4$ Amplitudenstufen.
- Bei der $\text{64-QAM}$ würde entsprechend $M = 8$ gelten und bei der $\text{256-QAM}$ ist die „eindimensionale” Stufenzahl $M = 16$.
- Alle im Kapitel Redundanzfreie Codierung des Buches "Digitalsignalübertragung" genannten Eigenschaften für redundanzfreie mehrstufige Signale gelten auch hier, wobei allerdings die Zusetzung der orthogoalen Trägerfrequenzsignale noch geeignet zu berücksichtigen ist.
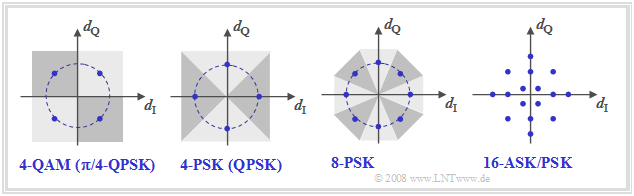
Other signal space constellations
Die Grafik zeigt weitere Signalraumkonstellationen. Links ist die 4–QAM nach der bisherigen Beschreibung dargestellt. Die Konstellation rechts daneben kennzeichnet eine vierstufige Phasenmodulation, die wir "4–PSK" bzw. "QPSK" nennen. Ein Vergleich dieser beiden linken Diagramme zeigt:
- Die hier als QPSK (Quaternary Phase Shift Keying ) bezeichnete Variante verwendet die Phasenlagen $0^\circ$, $90^\circ$, $180^\circ$ und $270^\circ$.
- Aus den eingezeichneten Entscheidungsgebieten erkennt man, dass hier die Detektion nicht auf zwei Binärentscheidungen zurückgeführt werden kann.
- Auch die 4–QAM (links) kann als vierstufige Phasenmodulation aufgefasst werden $($Phasenlagen $±45^\circ$, $±135^\circ)$.
- Gegenüber der QPSK ergibt sich eine Drehung um $±45^\circ$ $(π/4)$ ⇒ die 4–QAM oft auch als ${\rm π/4}\text{–QPSK}$ bezeichnet.
- Ähnlich wie man bei der BPSK durch Vorcodierung zur DPSK kommt, kann auch die 4–PSK zur 4–DPSK erweitert und dadurch die Demodulation erleichtert werden.
- Diese wurde zum Beispiel bei der Datenübertragung über Telefonkanäle gemäß CCITT–Empfehlung "V26" angewendet $($Trägerfrequenz $\text{1800 Hz}$, Datenrate $\text{2400 bit/s)}$.
Die beiden rechten Diagramme zeigen höherstufige Modulationsverfahren:
- Die 8–PSK (bzw. 8–DPSK) erlaubt entsprechend der CCITT–Empfehlung "V27" beim Telefonkanal eine Datenrate von bis zu $\text{4800 bit/s}$.
- Die Empfehlung "V29" sieht mit der 16–ASK/PSK eine hybride Modulationsform vor, die bei fest verschalteten Leitungen Datenraten bis $\text{9600 bit/s}$ ermöglicht.
Nyquist– und Wurzel–Nyquist–QAM–Systeme
Bisher wurde in diesem Kapitel aus Darstellungsgründen stets vom rechteckförmigen Sendegrundimpuls ausgegangen. In der Praxis verwendet man aber meist eine Wurzel–Nyquist–Charakteristik entsprechend der Beschreibung im Buch "Digitalsignalübertragung". In aller Kürze lassen sich diese Systeme wie folgt charakterisieren:
- Der Empfängerfrequenzgang $H_{\rm E}(f)$ wird hier formgleich mit dem (normierten) Sendeimpulsspektrum $H_{\rm S}(f)$ gewählt, was unter der Nebenbedingung der Leistungsbegrenzung (das heißt: bei konstanter mittlerer Sendeleistung) zur kleinstmöglichen Fehlerwahrscheinlichkeit führt.
- Der Gesamtfrequenzgang $H_{\rm Nyq}(f) = H_{\rm S}(f) · H_{\rm E}(f)$ erfüllt das erste Nyquistkriterium, so dass es beim Empfänger zu keinen Impulsinterferenzen kommt. $H_{\rm S}(f)$ und $H_{\rm E}(f)$ haben somit jeweils eine Wurzel–Nyquist–Charakteristik.
- Für den Frequenzgang $H_{\rm Nyq}(f)$ verwendet man einen Cosinus–Rolloff–Tiefpass $H_{\rm CRO}(f)$ mit der äquivalenten Bandbreite $Δf_{\rm CRO} = 1/T$ und frei wählbarem Rolloff–Faktor $(0 ≤ r ≤ 1)$. Das interaktive Applet Frequenzgang und Impulsantwort verdeutlicht den Frequenzgang und die Impulsantwort dieses Tiefpasses.
- Der Vorteil dieser Wurzel–Nyquist–Systeme ist die deutlich kleinere Bandbreite $(1 + r)/T$ gegenüber der bisher betrachteten Konfiguration mit rechteckförmigem $g_s(t)$ und rechteckförmigem $h_{\rm E}(t)$, dessen Spektrum (theoretisch) unendlich weit ausgedehnt ist.
- Hinsichtlich Fehlerwahrscheinlichkeit ändert sich gegenüber der Rechteck–Rechteck–Konfiguration nichts, da der Grundimpuls $g_d(t)$ vor dem Entscheider äquidistante Nulldurchgänge aufweist und somit Impulsinterferenzen vermieden werden.
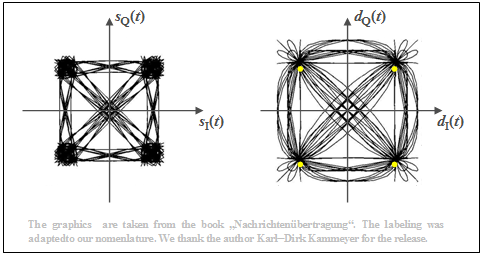
Die Grafik zeigt Phasendiagramme für diesen Fall, die dem Buch [Kam04][1] entnommen sind. Der Rolloff–Faktor beträgt $r = 0.5$. Man erkennt aus diesen Darstellungen:
- Das rechte Diagramm zeigt die Detektionssignale im $\rm I$– und $\rm Q$–Zweig nach den Wurzel–Nyquist–Empfangsfiltern in 2D–Darstellung. Die dazugehörigen Spektren besitzen jeweils cosinusförmige Flanken um die Nyquistfrequenz $f_{\rm Nyq} = 1/(2T)$.
- Zu den Detektionszeitpunkten sind im Phasendiagramm nur die vier gelb eingezeichneten Punkte möglich. Die Übergänge dazwischen sind vielfältig. Anzumerken ist, dass nur wenige Linien durch den Koordinaten-Nullpunkt gehen.
- Links dargestellt sind die beiden Sendesignale im äquivalenten Tiefpassbereich, $s_{\rm I}(t) = {\rm Re}\big[s_{\rm TP}(t)\big]$ und $s_{\rm Q}(t) = {\rm Im}\big[s_{\rm TP}(t)\big]$. Aufgrund der Wurzel–Nyquist–Spektralformung gibt es beim Sender Impulsinterferenzen, das heißt, dass das äquivalente Tiefpass–Signal $s_{\rm TP}(t) = s_{\rm I}(t) + {\rm j} · s_{\rm Q}(t)$ auch zu den Detektionszeitpunkten nicht auf vier Punkte beschränkt ist.
- Der Betrag $|s_{\rm TP}(t)|$ – also der Abstand vom Nullpunkt – gibt die Hüllkurve des 4–QAM–Signals an. Man erkennt aus dem linken Diagramm deutlich, dass es insbesondere bei Phasenänderungen um $π$ starke Amplitudeneinbrüche gibt, da $s_{\rm TP}(t)$ dann häufig auch (komplexe) Werte nahe Null annimmt.
Offset–Quadraturamplitudenmodulation
Ausgehend von den Gleichungen für die $\text{4–QAM}$ $($bzw. $π/4\text{–QPSK)}$ kommt man zur $\text{Offset–4–QAM}$, die wir vereinfachend mit $\text{Offset–QPSK}$ bezeichnen. Für das Sendesignal gilt hier:
- $$s(t) =s_{\rm I}(t) \cdot \cos(2 \pi f_{\rm T} t) - s_{\rm Q}(t) \cdot \sin(2 \pi f_{\rm T} t),$$
- $$\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s_{\rm I}(t) = \sum_{\nu = - \infty}^{+\infty}a_{\rm I\hspace{0.03cm}\it \nu} \cdot g_s (t - \nu \cdot T)\hspace{0.05cm},\hspace{0.5cm} s_{\rm Q}(t) = \sum_{\nu = - \infty}^{+\infty}a_{\rm Q\hspace{0.03cm}\it \nu} \cdot g_s (t -{T}/{2} - \nu \cdot T)\hspace{0.05cm}.$$
Der einzige, aber entscheidende Unterschied ist die zeitliche Verschiebung der Quadraturkomponente gegenüber der Inphasekomponente um eine halbe Symboldauer $(T/2)$. Dies hat den Vorteil, dass
- die Phasenfunktion nicht durch Null geht, und
- dadurch die Hüllkurve $|s_{\rm TP}(t)|$ deutlich weniger schwankt.
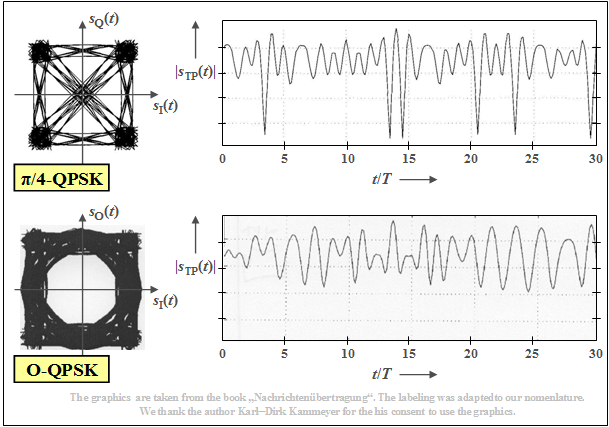
$\text{Beispiel 2:}$ Die obere Grafik zeigt
- links nochmals das Phasendiagramm für die $π/4\hspace{-0.05cm}-\hspace{-0.05cm}\text{QPSK}$,
- rechts daneben einen beispielhaften Verlauf der Hüllkurve, wobei wie im letzten Abschnitt ein Wurzel–Nyquist–Sendespektrum mit dem Rolloff–Faktor $r = 0.5$ zugrunde liegt.
Die unteren Bilder zeigen, dass die $\text{Offset – QPSK}$ hinsichtlich der Einhüllenden deutlich bessere Eigenschaften aufweist (weniger gravierende Signaleinbrüche).
Wesentliche Eigenschaften von 4–QAM/QPSK und Offset–QPSK können Sie sich mit dem interaktiven Applet QPSK und Offset-QPSK verdeutlichen, wobei als Grundimpuls alternativ wählbar ist:
- ein Rechteckimpuls,
- ein Cosinusimpuls,
- ein Nyquistimpuls,
- ein Wurzel–Nyquistimpuls.
Aufgaben zum Kapitel
Aufgabe 4.10: Signalverläufe der 16–QAM
Aufgabe 4.10Z: Signalraumkonstellation der 16–QAM
Aufgabe 4.11: Frequenzbereichsbetrachtung der 4–QAM
Aufgabe 4.11Z: Fehlerwahrscheinlichkeit bei QAM
Aufgabe 4.12: Wurzel–Nyquist–Systeme
Aufgabe 4.12Z: Nochmals 4–QAM–Systeme
Quellenverzeichnis
- ↑ Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004.