Aufgaben:Exercise 1.3: System Comparison at AWGN Channel

• Return to book

System comparison at AWGN channel

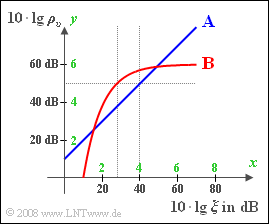
For the comparison of different modulation and demodulation methods with regard to noise sensitivity,  we usually assume the so-called  AWGN channel  and present the following double logarithmic diagram:

• The y-axis indicates the  "sink-to-noise ratio"  (logarithmic SNR)   ⇒   $10 · \lg ρ_v$  in dB.
•  $10 · \lg ξ$  is plotted on the x-axis;  the normalized power parameter  ("performance parameter")  is characterized by:

$$\xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$

• Thus,  the transmission power  $P_{\rm S}$,  the channel attenuation factor $α_{\rm K}$,  the noise power density  $N_0$  and the bandwidth  $B_{\rm NF}$  of the message signal are suitably summarised together in  $ξ$.
• Unless explicitly stated otherwise,  the following values shall be assumed in the exercise:

$$P_{\rm S}= 5 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm K} = 0.001\hspace{0.05cm}, \hspace{0.2cm} {N_0} = 10^{-10}\;{\rm W}/{\rm Hz}\hspace{0.05cm}, \hspace{0.2cm} B_{\rm NF}= 5\; {\rm kHz}\hspace{0.05cm}.$$

Two systems are plotted in the graph and their   $(x, y)$-curve can be described as follows:

• $\text{System A}$  is characterized by the following equation:

$$y = x+1.$$

•  $\text{System B}$  is instead characterized by:

$$y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right)\hspace{0.05cm}.$$

The additional axis labels drawn in green have the following meaning:

$$x = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\xi} {10 \,{\rm dB}}\hspace{0.05cm}, \hspace{0.3cm}y = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\rho_v} {10 \,{\rm dB}}\hspace{0.05cm}.$$

• Thus  $x = 4$  represents  $10 · \lg ξ = 40\text{ dB}$  or  $ξ = 10^4$ 
• and  $y = 5$  represents  $10 · \lg ρ_v= 50\text{ dB}$ , i.e.,  $ρ_v = 10^5$.

Hints:

• This exercise belongs to the chapter   Quality Criteria.
• Particular reference is made to the page   Investigating at the AWGN channel.
• By specifying the powers in watts,  they are independent of the reference resistance  $R$.

Questions

1

What is the  sink signal-to-noise ratio  (in dB)  for  $\text{System A}$  with  $P_{\rm S}= 5 \;{\rm kW}$,   $\alpha_{\rm K} = 0.001$,   $N_0 = 10^{-10}\;{\rm W}/{\rm Hz}$,   $B_{\rm NF}= 5\; {\rm kHz}$?

$10 · \lg \hspace{0.05cm}ρ_v \ = \ $ $\ \text{dB}$

2

Now  $10 · \lg \hspace{0.05cm} ρ_v ≥ 60\text{ dB}$  is required.  Which independent measures can be taken to achieve this?

	Increasing the transmission power from  $P_{\rm S}= 5\text{ kW}$  to $10\text{ kW}$ .
	Increasing the channel transmission factor from  $α_{\rm K} = 0.001$  to  $0.004$.
	Reducing the noise power density to  $N_0=10^{–11 }\text{ W/Hz}$.
	Increasing the source signal bandwidth from  $B_{\rm NF}= 5\text{ kHz}$  to  $10\text{ kHz}$.

3

What is the sink signal-to-noise ratio for  $\text{System B}$  with  $10 · \lg ξ = 40\text{ dB}$?

$10 · \lg \hspace{0.05cm}ρ_v \ = \ $ $\ \text{dB}$

4

If the required sink signal-to-noise ratio is  $10 · \lg ρ_v = 50\text{ dB}$,  what transmission power  $P_{\rm S}$ is sufficient to achieve this for  $\text{System B}$?

$P_{\rm S} \ = \ $ $\ \text{ kW }$

5

What value of  $10 · \lg ξ$  gives the greatest improvement of  $\text{System B}$  relative to  $\text{System A}$ ?

$10 · \lg \hspace{0.05cm} ξ \ = \ $ $\ \text{dB}$

Solution

Solution

(1)  The normalized performance parameter is calculated using these values as follows:

$$\xi = \frac{5 \cdot 10^3\,{\rm W}\cdot 10^{-6} }{10^{-10}\,{\rm W}/{\rm Hz} \cdot 5 \cdot 10^3\,{\rm Hz}} = 10^4 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = 40\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x=4 \hspace{0.05cm}.$$

• This gives the auxiliary coordinate value  $y = 5$,  which leads to a sink SNR of   $10 · \lg \hspace{0.05cm} ρ_v\hspace{0.15cm}\underline{ = 50 \ \rm dB}$.

(2) Answers 2 and 3  are correct:

This requirement corresponds to a  $10$  dB  increase in the sink SNR compared to the previous system,  so  $10 · \lg \hspace{0.05cm}ξ$  must also be increased by $10$  dB:

$$10 \cdot {\rm lg} \hspace{0.1cm}\xi = 50\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \xi=10^5 \hspace{0.05cm}.$$

A tenfold larger  $ξ$  value is achieved  (provided all other parameters are held constant in each case)

• by a transmission power of  $P_{\rm S} = 50$  kW  instead of   $5$  kW,
• by a channel transmission factor of   $α_{\rm K} = 0.00316$  instead of  $0.001$,
• by a noise power density of   $N_0 = 10^{ –11 }$  W/Hz  instead of  $10^{ –10 }$  W/Hz,
• by a signal bandwidth of  $B_{\rm NF} = 0.5$  kHz  instead of   $5$  kHz.

(3)  For  $10 · \lg \hspace{0.05cm} ξ = 40$  dB,  the auxiliary value is   $x = 4$.  This gives the auxiliary  $y$–value:

$$y= 6 \cdot \left(1 - {\rm e}^{-3} \right)\approx 5.7 \hspace{0.05cm}.$$

• This corresponds to a sink SNR of   $10 · \lg \hspace{0.05cm} ρ_v\hspace{0.15cm}\underline{ = 57 \ \rm dB}$   ⇒   $7$  dB improvement over  $\text{System A}$.

(4)  This problem is described by the following equation:

$$y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right) = 5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm e}^{-x+1} ={1}/{6}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} x = 1+ {\rm ln} \hspace{0.1cm}6 \approx 2.79 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = 27.9\,{\rm dB}\hspace{0.05cm}.$$

• For  $\text{System A}$  $10 · \lg \hspace{0.05cm} \xi = 40$  dB is required,  which was achieved with   $P_{\rm S} = 5$  kW and the other numerical values given. 
• Now the transmission power can be reduced by about   $12.1$  dB:

$$10 \cdot {\rm lg} \hspace{0.1cm} \frac{P_{\rm S}}{ 5 \;{\rm kW}}= -12.1\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{P_{\rm S}}{ 5 \;{\rm kW}} = 10^{-1.21}\approx 0.06\hspace{0.05cm}.$$

• This means that in  $\text{System B}$  the same system quality is achieved with only   $6\%$  of the transmission power of  $\text{System A}$  – i.e., with only   $P_{\rm S} \hspace{0.15cm}\underline{ = 0.3 \ \rm kW}$.

(5)  The larger sink SNR of  $\text{System B}$  compared to  $\text{System A}$  we will denote with   $V$  (from German  "Verbesserung"   ⇒   "improvement"):

$$V = 10 \cdot {\rm lg} \hspace{0.1cm}\rho_v \hspace{0.1cm}{\rm (System\;B)} - 10 \cdot {\rm lg} \hspace{0.1cm}\rho_v \hspace{0.1cm}{\rm (System\;A)} = \left[6 \cdot \left(1 - {\rm e}^{-x+1} \right) -x -1 \right] \cdot 10\,{\rm dB}\hspace{0.05cm}.$$

• Setting the derivative to zero yields the  $x$–value that leads to the maximum improvement:

$$\frac{{\rm d}V}{{\rm d}x} = 6 \cdot {\rm e}^{-x+1} -1\Rightarrow \hspace{0.3cm} x = 1+ {\rm ln} \hspace{0.1cm}6 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = \hspace{0.15cm}\underline {27.9\,{\rm dB}}\hspace{0.05cm}.$$

• This results in exactly the case discussed in subtask   (4)  with   $10 · \lg ρ_υ = 50$  dB,  while the sink SNR for  $\text{System A}$  is only  $37.9$  dB. 
• The improvement is therefore  $12.1$  dB.