Difference between revisions of "Aufgaben:Exercise 2.4: Dual Code and Gray Code"
| Line 71: | Line 71: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
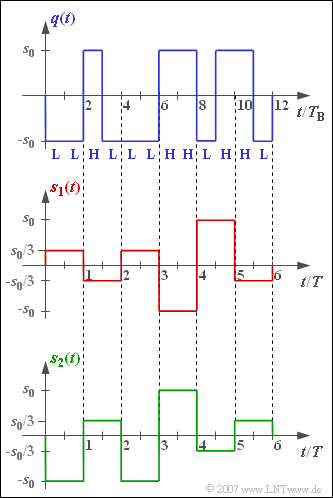
| − | '''(1)''' In the signal $s_{2}(t)$ one recognizes the realization of the dual code indicated at the beginning. On the other hand, in the signal $s_{2}(t)$ a | + | '''(1)''' In the signal $s_{2}(t)$ one recognizes the realization of the dual code indicated at the beginning. On the other hand, in the signal $s_{2}(t)$ a Gray code $\Rightarrow$ <u>solution 1</u> with the following mapping was used: |
:$$\mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1, \hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1/3, \hspace{0.35cm} \mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1/3, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1 \hspace{0.05cm}.$$ | :$$\mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1, \hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1/3, \hspace{0.35cm} \mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1/3, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1 \hspace{0.05cm}.$$ | ||
| − | '''(2)''' Let the probability $p$ that the amplitude value $3 \, \rm V$ falls below the adjacent decision threshold $2\, \rm V$ due to the Gaussian distributed noise with standard deviation $\sigma_{d}$ be $1\, \%$. It follows that: | + | '''(2)''' Let the probability $p$ that the amplitude value $3 \, \rm V$ falls below the adjacent decision threshold $2\, \rm V$ due to the Gaussian distributed noise with standard deviation $\sigma_{d}$ be $1\, \%$. It follows that: |
:$$ p = {\rm Q} \left ( \frac{3\,{\rm V} - 2\,{\rm V}} { \sigma_d}\right ) = 1 \%\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {1\,{\rm V} }/ { \sigma_d} \approx 2.33 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \sigma_d}\hspace{0.15cm}\underline {\approx 0.43\,{\rm V}}\hspace{0.05cm}.$$ | :$$ p = {\rm Q} \left ( \frac{3\,{\rm V} - 2\,{\rm V}} { \sigma_d}\right ) = 1 \%\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {1\,{\rm V} }/ { \sigma_d} \approx 2.33 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \sigma_d}\hspace{0.15cm}\underline {\approx 0.43\,{\rm V}}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' The two outer symbols are each | + | '''(3)''' The two outer symbols are each falsified with probability $p$, the two inner symbols with double probability $(2p)$. By averaging considering equal symbol occurrence probabilities, we obtain |
:$$p_{\rm S} = 1.5 \cdot p \hspace{0.15cm}\underline { = 1.5 \,\%} \hspace{0.05cm}.$$ | :$$p_{\rm S} = 1.5 \cdot p \hspace{0.15cm}\underline { = 1.5 \,\%} \hspace{0.05cm}.$$ | ||
| − | '''(4)''' Each symbol error results in exactly one bit error. However, since each quaternary symbol contains exactly two binary symbols, the bit error probability is obtained: | + | '''(4)''' Each symbol error results in exactly one bit error. However, since each quaternary symbol contains exactly two binary symbols, the bit error probability is obtained: |
:$$p_{\rm B} = {p_{\rm S}}/ { 2}\hspace{0.15cm}\underline { = 0.75 \,\%} \hspace{0.05cm}.$$ | :$$p_{\rm B} = {p_{\rm S}}/ { 2}\hspace{0.15cm}\underline { = 0.75 \,\%} \hspace{0.05cm}.$$ | ||
| − | '''(5)''' When calculating the symbol error probability $p_{\rm S}$, the mapping used is not taken into account. As in subtask '''(3)''', we obtain $p_{\rm S} \hspace{0.15cm}\underline{ = 1.5 \, \%}$. | + | '''(5)''' When calculating the symbol error probability $p_{\rm S}$, the mapping used is not taken into account. As in subtask '''(3)''', we obtain $p_{\rm S} \hspace{0.15cm}\underline{ = 1.5 \, \%}$. |
| − | '''(6)''' The two outer symbols are | + | '''(6)''' The two outer symbols are falsified with $p$ and lead to only one bit error each even with dual code. |
| − | * The inner symbols are | + | * The inner symbols are falsified with $2p$ and now lead to $1.5$ bit errors on average. |
| − | *Taking into account the factor $2$ in the denominator – see subtask '''(2)''' – we thus obtain for the bit error probability of the dual code: | + | *Taking into account the factor $2$ in the denominator – see subtask '''(2)''' – we thus obtain for the bit error probability of the dual code: |
:$$p_{\rm B} = \frac{1} { 4} \cdot \frac{p + 2p \cdot 1.5 + 2p \cdot 1.5 + p} { 2} = p \hspace{0.15cm}\underline { = 1 \,\%} \hspace{0.05cm}.$$ | :$$p_{\rm B} = \frac{1} { 4} \cdot \frac{p + 2p \cdot 1.5 + 2p \cdot 1.5 + p} { 2} = p \hspace{0.15cm}\underline { = 1 \,\%} \hspace{0.05cm}.$$ | ||
Revision as of 15:28, 16 May 2022
The two shown signals $s_{1}(t)$ and $s_{2}(t)$ are two different realizations of a redundancy-free quaternary transmitted signal, both derived from the blue drawn binary source signal $q(t)$.
For one of the transmitted signals, the so-called dual code with mapping
- $$\mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0/3,\hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0/3, \hspace{0.35cm} \mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0$$
was used, for the other one a certain form of a Gray code. This is characterized by the fact that the binary representation of adjacent amplitude values always differ only in a single bit.
The solution of the exercise should be based on the following assumptions:
- The amplitude levels are $±3\, \rm V$ and $±1 \, \rm V$.
- The decision thresholds lie in the middle between two adjacent amplitude values, i.e. at $–2\, \rm V$, $0\, \rm V$ and $+2\, \rm V$.
- The noise rms value $\sigma_{d}$ is to be chosen so that the falsification probability from the outer symbol $(+s_0)$ to the nearest symbol $(+s_{0}/3)$ is exactly $p = 1\%$.
- Falsification to non-adjacent symbols can be excluded; in the case of Gaussian perturbations, this simplification is always allowed in practice.
One distinguishes in principle between
- the "symbol error probability" $p_{\rm S}$ (related to the quaternary signal) and
- the "bit error probability" $p_{B}$ (related to the binary source signal).
Notes:
- The exercise is part of the chapter "Basics of Coded Transmission".
- Reference is also made to the chapter "Redundancy-Free Coding".
- For numerical evaluation of the Q–function you can use the HTML5/JavaScript applet Complementary Gaussian Error Functions.
Questions
Solution
- $$\mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1, \hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1/3, \hspace{0.35cm} \mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1/3, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1 \hspace{0.05cm}.$$
(2) Let the probability $p$ that the amplitude value $3 \, \rm V$ falls below the adjacent decision threshold $2\, \rm V$ due to the Gaussian distributed noise with standard deviation $\sigma_{d}$ be $1\, \%$. It follows that:
- $$ p = {\rm Q} \left ( \frac{3\,{\rm V} - 2\,{\rm V}} { \sigma_d}\right ) = 1 \%\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {1\,{\rm V} }/ { \sigma_d} \approx 2.33 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \sigma_d}\hspace{0.15cm}\underline {\approx 0.43\,{\rm V}}\hspace{0.05cm}.$$
(3) The two outer symbols are each falsified with probability $p$, the two inner symbols with double probability $(2p)$. By averaging considering equal symbol occurrence probabilities, we obtain
- $$p_{\rm S} = 1.5 \cdot p \hspace{0.15cm}\underline { = 1.5 \,\%} \hspace{0.05cm}.$$
(4) Each symbol error results in exactly one bit error. However, since each quaternary symbol contains exactly two binary symbols, the bit error probability is obtained:
- $$p_{\rm B} = {p_{\rm S}}/ { 2}\hspace{0.15cm}\underline { = 0.75 \,\%} \hspace{0.05cm}.$$
(5) When calculating the symbol error probability $p_{\rm S}$, the mapping used is not taken into account. As in subtask (3), we obtain $p_{\rm S} \hspace{0.15cm}\underline{ = 1.5 \, \%}$.
(6) The two outer symbols are falsified with $p$ and lead to only one bit error each even with dual code.
- The inner symbols are falsified with $2p$ and now lead to $1.5$ bit errors on average.
- Taking into account the factor $2$ in the denominator – see subtask (2) – we thus obtain for the bit error probability of the dual code:
- $$p_{\rm B} = \frac{1} { 4} \cdot \frac{p + 2p \cdot 1.5 + 2p \cdot 1.5 + p} { 2} = p \hspace{0.15cm}\underline { = 1 \,\%} \hspace{0.05cm}.$$