Difference between revisions of "Aufgaben:Exercise 3.10: Maximum Likelihood Tree Diagram"
| Line 3: | Line 3: | ||
[[File:P_ID1465__Dig_A_3_10_95.png|right|frame|Signals and tree diagram]] | [[File:P_ID1465__Dig_A_3_10_95.png|right|frame|Signals and tree diagram]] | ||
| − | As in [[Aufgaben:Exercise_3.09:_Correlation_Receiver_for_Unipolar_Signaling|"Exercise 3.9"]] we consider the joint decision of three binary symbols (bits) by means of the correlation receiver. | + | As in [[Aufgaben:Exercise_3.09:_Correlation_Receiver_for_Unipolar_Signaling|"Exercise 3.9"]] we consider the joint decision of three binary symbols ("bits") by means of the correlation receiver. |
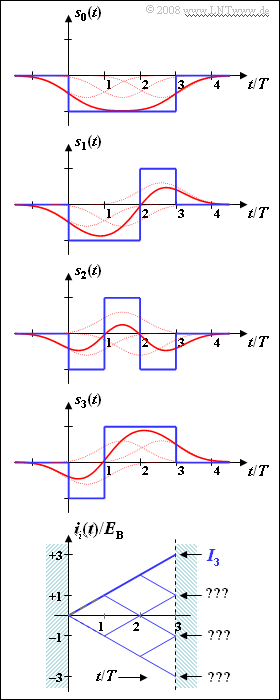
*The possible transmitted signals $s_0(t), \ \text{...} \ , \ s_7(t)$ are bipolar. | *The possible transmitted signals $s_0(t), \ \text{...} \ , \ s_7(t)$ are bipolar. | ||
| + | |||
*In the graphic the functions $s_0(t)$, $s_1(t)$, $s_2(t)$ and $s_3(t)$ are shown. | *In the graphic the functions $s_0(t)$, $s_1(t)$, $s_2(t)$ and $s_3(t)$ are shown. | ||
| + | |||
*The blue curves are valid for rectangular NRZ transmission pulses. | *The blue curves are valid for rectangular NRZ transmission pulses. | ||
| − | Below is drawn the so-called tree diagram for this constellation under the condition that the signal $s_3(t)$ was | + | Below is drawn the so-called "tree diagram" for this constellation under the condition that the signal $s_3(t)$ was sent. Shown here in the range from $0$ to $3T$ are the functions |
:$$i_i(t) = \int_{0}^{t} s_3(\tau) \cdot s_i(\tau) \,{\rm d} | :$$i_i(t) = \int_{0}^{t} s_3(\tau) \cdot s_i(\tau) \,{\rm d} | ||
\tau \hspace{0.3cm}( i = 0, \ \text{...} \ , 7)\hspace{0.05cm}.$$ | \tau \hspace{0.3cm}( i = 0, \ \text{...} \ , 7)\hspace{0.05cm}.$$ | ||
| − | *The correlation receiver compares the final values $I_i = i_i(3T)$ with each other and searches for the largest possible value $I_j$. | + | *The correlation receiver compares the final values $I_i = i_i(3T)$ with each other and searches for the largest possible value $I_j$. |
| + | |||
*The corresponding signal $s_j(t)$ is then the one most likely to have been sent according to the maximum likelihood criterion. | *The corresponding signal $s_j(t)$ is then the one most likely to have been sent according to the maximum likelihood criterion. | ||
| + | *Note that the correlation receiver generally makes the decision based on the corrected quantities | ||
| + | :$$W_i = I_i \ - E_i/2.$$ | ||
| + | *But since for bipolar rectangles all transmitted signals $(i = 0, \ \text{...} \ , \ 7)$ have exactly the same energy | ||
| + | :$$E_i = \int_{0}^{3T} s_i^2(t) \,{\rm d} t,$$ | ||
| − | + | :the integrals $I_i$ provide exactly the same maximum likelihood information as the corrected quantities $W_i$. | |
| − | : | ||
| − | |||
| − | the integrals $I_i$ provide exactly the same maximum likelihood information as the corrected quantities $W_i$. | ||
The red signal waveforms $s_i(t)$ are obtained from the blue ones by convolution with the impulse response $h_{\rm G}(t)$ of a Gaussian low-pass filter with cutoff frequency $f_{\rm G} \cdot T = 0.35$. | The red signal waveforms $s_i(t)$ are obtained from the blue ones by convolution with the impulse response $h_{\rm G}(t)$ of a Gaussian low-pass filter with cutoff frequency $f_{\rm G} \cdot T = 0.35$. | ||
*Each individual rectangular pulse is broadened. | *Each individual rectangular pulse is broadened. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | *The red signal waveforms lead to "intersymbol interference" in case of threshold decision. | ||
| − | + | Note: The exercise belongs to the chapter [[Digital_Signal_Transmission/Optimal_Receiver_Strategies|"Optimal Receiver Strategies"]]. | |
| − | |||
| Line 39: | Line 39: | ||
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Give the following normalized final values $I_i/E_{\rm B}$ for rectangular signals (without noise). | + | {Give the following normalized final values $I_i/E_{\rm B}$ for rectangular signals $($without noise$)$. |
|type="{}"} | |type="{}"} | ||
$I_0/E_{\rm B} \ = \ $ { -1.03--0.97 } | $I_0/E_{\rm B} \ = \ $ { -1.03--0.97 } | ||
| Line 49: | Line 49: | ||
|type="[]"} | |type="[]"} | ||
- The tree diagram can be further described by straight line segments. | - The tree diagram can be further described by straight line segments. | ||
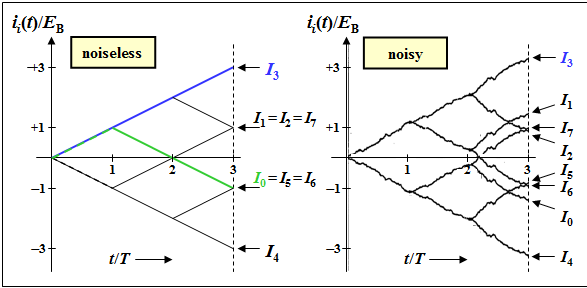
| − | + If $I_3$ is the maximum $I_i$ value, the receiver decides correctly. | + | + If $I_3$ is the maximum $I_i$ value, the receiver decides correctly. |
| − | - $I_0 = I_6$ is valid independent of the strength of the noise. | + | - $I_0 = I_6$ is valid independent of the strength of the noise. |
| − | {Which statements are valid for the red signal waveforms (with intersymbol interference)? | + | {Which statements are valid for the red signal waveforms $($with intersymbol interference$)$? |
|type="[]"} | |type="[]"} | ||
- The tree diagram can be further described by straight line segments. | - The tree diagram can be further described by straight line segments. | ||
Revision as of 17:07, 30 June 2022
As in "Exercise 3.9" we consider the joint decision of three binary symbols ("bits") by means of the correlation receiver.
- The possible transmitted signals $s_0(t), \ \text{...} \ , \ s_7(t)$ are bipolar.
- In the graphic the functions $s_0(t)$, $s_1(t)$, $s_2(t)$ and $s_3(t)$ are shown.
- The blue curves are valid for rectangular NRZ transmission pulses.
Below is drawn the so-called "tree diagram" for this constellation under the condition that the signal $s_3(t)$ was sent. Shown here in the range from $0$ to $3T$ are the functions
- $$i_i(t) = \int_{0}^{t} s_3(\tau) \cdot s_i(\tau) \,{\rm d} \tau \hspace{0.3cm}( i = 0, \ \text{...} \ , 7)\hspace{0.05cm}.$$
- The correlation receiver compares the final values $I_i = i_i(3T)$ with each other and searches for the largest possible value $I_j$.
- The corresponding signal $s_j(t)$ is then the one most likely to have been sent according to the maximum likelihood criterion.
- Note that the correlation receiver generally makes the decision based on the corrected quantities
- $$W_i = I_i \ - E_i/2.$$
- But since for bipolar rectangles all transmitted signals $(i = 0, \ \text{...} \ , \ 7)$ have exactly the same energy
- $$E_i = \int_{0}^{3T} s_i^2(t) \,{\rm d} t,$$
- the integrals $I_i$ provide exactly the same maximum likelihood information as the corrected quantities $W_i$.
The red signal waveforms $s_i(t)$ are obtained from the blue ones by convolution with the impulse response $h_{\rm G}(t)$ of a Gaussian low-pass filter with cutoff frequency $f_{\rm G} \cdot T = 0.35$.
- Each individual rectangular pulse is broadened.
- The red signal waveforms lead to "intersymbol interference" in case of threshold decision.
Note: The exercise belongs to the chapter "Optimal Receiver Strategies".
Questions
Solution
The correct results are thus:
- $$I_0/E_{\rm B}\hspace{0.15cm}\underline { = -1},$$
- $$I_2/E_{\rm B} \hspace{0.15cm}\underline {= +1}, $$
- $$I_4/E_{\rm B} \hspace{0.15cm}\underline {= -3}, $$
- $$I_6/E_{\rm B}\hspace{0.15cm}\underline { = -1} \hspace{0.05cm}.$$
(2) Only the second solution is correct:
- In the presence of (noise) disturbances, the functions $i_i(t)$ no longer increase or decrease linearly, but have a curve as shown in the right graph.
- As long as $I_3 > I_{\it i≠3}$, the correlation receiver decides correctly.
- In the presence of noise, $I_0 ≠ I_6$ always holds, in contrast to the noise-free tree diagram.
(3) Only the second statement is true:
- Since now the possible transmitted signals $s_i(t)$ can no longer be composed of isolated horizontal sections, also the tree diagram without noise does not consist of straight line segments.
- Since the energies $E_i$ are different – this can be seen, for example, by comparing the (red) signals $s_0(t)$ and $s_2(t)$ – it is essential to use the corrected quantities $W_i$ for the decision.
- The use of the pure correlation values $I_i$ can already lead to wrong decisions without noise disturbances.
(4) Answer 1 is correct:
- In the case without intersymbol interference (blue rectangular signals), all signals are limited to the range $0 \ ... \ 3T$.
- Outside this range the received signal $r(t)$ is pure noise.
- Therefore in this case also the integration over the range $0 \ \text{...} \ 3T$.
- In contrast, when intersymbol interference (red signals) is taken into account, the integrands $s_3(t) \cdot s_i(t)$ also differ outside this range.
- Therefore, if $t_1 = \ –T$ and $t_2 = +4T$ are chosen, the error probability of the correlation receiver is further reduced compared to the integration range $0 \ \text{...} \ 3T$ is further reduced.