Aufgaben:Exercise 3.11: Viterbi Receiver and Trellis Diagram

• Return to book

Trellis diagram
for one precursor

The Viterbi receiver allows a low-effort realization of the maximum likelihood decision rule.  It contains the system components listed below:

• A matched filter adapted to the basic transmission pulse with frequency response  $H_{\rm MF}(f)$  and output signal   $m(t)$,

• a sampler spaced at the symbol duration  $T$,  which converts the continuous-time signal   $m(t)$  into the discrete-time sequence   $〈m_{\rm \nu}〉$, 

• a decorrelation filter with frequency response   $H_{\rm DF}(f)$  for removing statistical ties between noise components of the sequence   $〈d_{\rm \nu}〉$,

• the Viterbi decision,  which uses a trellis-based algorithm to obtain the sink symbol sequence  $〈v_{\rm \nu}〉$. 

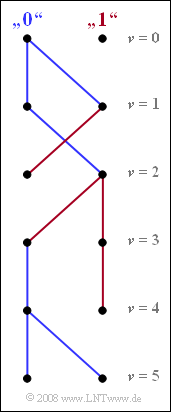
The graph shows the simplified trellis diagram of the two states  "$0$"  and  "$1$"  for time points   $\nu ≤ 5$.  This diagram is obtained as a result of evaluating the two minimum accumulated metrics   ${\it \Gamma}_{\rm \nu}(0)$  and  ${\it \Gamma}_{\rm \nu}(1)$  corresponding to   Exercise 3.11Z.

Notes:

• The exercise belongs to the chapter  "Viterbi Receiver".

• Reference is also made to the section  "Maximum-a-posteriori and Maximum–Likelihood decision rule".

• All quantities here are to be understood normalized. Also assume unipolar and equal probability amplitude coefficients:  

$${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5.$$

• The topic is also covered with the interactive SWF applet  "Properties of the Viterbi Receiver".

Questions

1

Which of the following statements are true?

	The matched filter  $H_{\rm MF}(f)$  is mainly used for noise power limitation.
	The decorrelation filter removes ties between samples.
	The noise power is only affected by  $H_{\rm MF}(f)$,  not by  $H_{\rm DF}(f)$.

2

At what times  $\nu$  can we finally decide the current symbol  $a_{\rm \nu}$? 

	$\nu = 1,$
	$\nu = 2,$
	$\nu = 3,$
	$\nu = 4,$
	$\nu = 5.$

3

What is the total sequence decided by the Viterbi receiver?

$a_1 \ = \ $

$a_2 \ = \ $

$a_3 \ = \ $

$a_4 \ = \ $

$a_5 \ = \ $

4

Which of the following statements are true?

	It is certain that the detected sequence was also sent.
	A MAP receiver would have the same error probability.
	Threshold decision is the same as this maximum likelihood receiver.

Solution

Solution

(1)  The first two solutions are correct:

• The signal $m(t)$ after the matched filter $H_{\rm MF}(f)$ has the largest possible signal-to-interference power ratio.
• However, the noise components of the sequence $〈m_{\rm \nu}〉$ are (strongly) correlated due to the spectral shaping.
• The task of the discrete-time decorrelation filter with the frequency response $H_{\rm DF}(f)$ is to dissolve these bonds, which is why the name "whitening filter" is also used for $H_{\rm DF}(f)$.
• However, this is possible only at the cost of increased noise power   ⇒   consequently, the last proposed solution does not apply.

(2)  The two arrows arriving at $\underline {\nu = 1}$ are each drawn in blue and indicate the symbol $a_1 = 0$. Thus, the initial symbol $a_1$ is already fixed at this point. Similarly, the symbols $a_3 = 1$ and $a_5 = 0$ are already fixed at the timesn $\underline {\nu = 3}$ and $\underline {\nu = 5}$, respectively.

In contrast, at time $\nu = 2$, a decision regarding symbol $a_2$ is not possible.

• Under the hypothesis that the following symbol $a_3 = 0$ would result in symbol $a_2 = 1$ (at "$0$" a red path arrives, thus coming from "$1$").
• In contrast, the hypothesis $a_3 = 1$ leads to the result $a_2 = 0$ (the path arriving at "$1$" is blue).

The situation is similar at time $\nu = 4$.

(3)  From the continuous paths at $\nu = 5$ it can be seen:

$$a_{1}\hspace{0.15cm}\underline {=0} \hspace{0.05cm},\hspace{0.2cm} a_{2}\hspace{0.15cm}\underline { =0} \hspace{0.05cm},\hspace{0.2cm}a_{3}\hspace{0.15cm}\underline {=1} \hspace{0.05cm},\hspace{0.2cm} a_{4}\hspace{0.15cm}\underline {=0} \hspace{0.05cm},\hspace{0.2cm} a_{5}\hspace{0.15cm}\underline {=0} \hspace{0.05cm}.$$

(4)  Only the second statement is correct:

• Since the source symbols "$0$" and "$1$" were assumed to be equally probable, the ML receiver (Viterbi) is identical to the MAP receiver.
• A threshold decision (which makes a symbol-by-symbol decision at each clock) has the same error probability as the Viterbi receiver only if there is no intersymbol interference.
• This is obviously not the case here, otherwise it should be possible to make a final decision at every time $\nu$.
• The first statement is also not true. Indeed, this would mean that the Viterbi receiver can have error probability $0$ in the presence of statistical noise. This is not possible for information-theoretic reasons.