Difference between revisions of "Aufgaben:Exercise 1.4: AMI and MMS43 Code"

Revision as of 16:21, 9 October 2022

Modified AMI code and MMS43 code

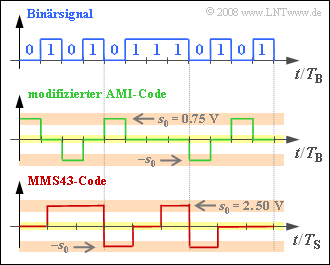
Two different ternary transmission codes are used with ISDN, which are to be clarified in the diagram at an exemplary binary input signal.

The upper diagram shows 12 bits $($each with the bit duration $T_{\rm B})$.

On the $\rm S_{0}$ interface (between NTBA and terminal equipment) the modified AMI code is used. The difference to the conventional AMI code is the swapping $0 \Leftrightarrow 1$ of the binary input signal.
In contrast, the MMS43 code (Modified Monitoring Sum 4B3T) is used on the $\rm U_{K0}$ interface, where four binary symbols are replaced by three ternary symbols $($voltage values $0 \ {\rm V}, +2.5 \ {\rm V}$ and $-2.5 \ {\rm V})$. The assignment is done depending on the previously coded symbols.

Notes:

The exercise belongs to the chapter "ISDN Basic Access".
Information on the MMS43 code can be found in the chapter "Block Coding with 4B3T Codes" of the book "Digital Signal Transmission".
Information on the AMI code can be found in the chapter "Symbolwise Coding with Pseudo-Ternary Codes" of the same book.

Questions

	Symbol duration $T_{\rm S}$ and bit duration $T_{\rm B}$ of the binary signal are the same.
	The encoding is done symbol by symbol.
	Each binary "0" is represented by $0 \hspace{0.1cm} \rm V$.
	The binary "1" is alternately represented by $+s_{0}$ and $-s_{0}$.

$r_{\rm AMI} \ = \ $

$\ \%$

$P_{\rm S, \ AMI} \ = \ $

$\ \rm mW$

	Symbol duration $T_{\rm S}$ and bit duration $T_{\rm B}$ of the binary signal are the same.
	The encoding is done block by block.
	Each binary "0" is represented by $0 \hspace{0.1cm} \rm V$.

$r_{\rm MMS43} \ = \ $

$\ \%$

$R_{\rm U_{K0}} \ = \ $

$\ \rm ternary \ symbols/second$

$P_{\rm S,\ MMS43} \ = \ $

$\ \rm mW$

Solution

(1) The first two statements are correct:

The modified AMI code is a so-called pseudo-ternary code with $T_{\rm S} = T_{\rm B}$ and symbol-wise coding.
The stated assignments apply to the conventional AMI code.
On the other hand, in the modified AMI code the binary "1" is represented by the voltage value $0 \ \rm V$ and the binary "0" alternately by $+s_{0}$ bzw. $-s_{0}$, where for $s_{0} = 0.75 \ \rm V$ is to be set.

(2)

The equivalent bit rate of the AMI encoded signal is $R_{\rm C} = {\rm log_2}\hspace{0.05cm}(3)/T_{\rm S}$; the bit rate of the redundancy-free binary source signal is equal to $R_{\rm B} = 1/T_{\rm B}$.
With $T_{\rm S} = T_{\rm B}$, according to the chapter "Basics of Coded Transmission" of the book "Digital Signal Transmission", we obtain for the (relative) redundancy of the modified AMI code:

$$r_{\rm AMI} = \frac{R_{\rm C}-R_{\rm B}}{R_{\rm C}} = 1 - \frac{1}{{\rm ld}\,(3)} \hspace{0.15cm}\underline{\approx 36.9\,\%} \hspace{0.05cm}.$$

(3)

Using the unit impedance $R = 1 \ \rm \Omega $, the following applies to the transmit power (with the unit $\rm V^{2}$):

$$P_{\rm S,\,AMI} = {1}/{2} \cdot {s_0}^2 = {1}/{2} \cdot {0.75\,{\rm V}}^2 \approx 0.28\,{\rm V^2} \hspace{0.05cm}.$$

Here it is considered that the AMI encoded signal is equal to $0 \ \rm V$ in half of the time.
Finally, considering the impedance $R = 100 \ \rm \Omega$, we get:

$$P_{\rm S,\,AMI} = \frac{0.28\,{\rm V^2}}{100\,\Omega} \hspace{0.15cm}\underline{ = 2.8\,{\rm mW}} \hspace{0.05cm}.$$

(4) The MMS43 code actually operates in blocks, with $m_{q} = 4 \ \rm binary \ symbols$ replaced by $m_{c} = 3 \ \rm ternary \ symbols$:

$$4 \cdot T_{\rm B} = 3 \cdot T_{\rm S}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm S} = {4}/{3} \cdot T_{\rm B} \hspace{0.05cm}.$$

Das heißt: That means: The first solution does not apply as well as the last one. Only solution 2 is correct:
In block coding, the binary symbol "0" cannot be uniformly replaced by the same code symbol.
Rather, the encoding can be described as follows, assuming the running digital sum ${\it \Sigma}_{0} = 0$ at the beginning (see graphic in the information section):

$$\mathbf{0 1 0 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{0 + +}\hspace{0.2cm}({\it \Sigma}_1 = 2)\hspace{0.05cm},$$

$$ \mathbf{0 1 1 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{- \,0 \,\,+}\hspace{0.2cm}({\it \Sigma}_2 = 2)\hspace{0.05cm},$$

$$ \mathbf{0 1 0 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{- \,0\,\,\, 0}\hspace{0.2cm}({\it \Sigma}_3 = 1) \hspace{0.05cm}.$$

"Exercise 1.4Z" discusses the MMS43 code in more detail.

(5) The MMS43 code belongs to the class of 4B3T codes. For these it is valid:

$$R_{\rm B} = \frac{1}{T_{\rm B}}, \hspace{0.2cm} R_{\rm C} = \frac{{\rm ld}\,(3)}{T_{\rm S}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}r_{\rm MMS43} = 1 - \frac{R_{\rm B}}{R_{\rm C}} = 1 - \frac{T_{\rm S}/T_{\rm B}}{{\rm ld}\,(3)} = 1 - \frac{4/3}{{\rm log_2}\,(3)} \hspace{0.15cm}\underline{\approx 15.9\,\%} \hspace{0.05cm}.$$

(6) The following number of ternary symbols are transmitted on the $\rm U_{K0}$ bus per millisecond:

Channel B1: 64 binary symbols ⇒ 48 ternary symbols,
Channel B2: 64 binary symbols ⇒ 48 ternary symbols,
D channel: 16 binary symbols ⇒ 12 ternary symbols,
Synchronization and control symbols ⇒ 12 ternary symbols.

As a sum, this results in 120 ternary symbols per millisecond or 120,000 ternary symbols per second.

(7) Considering the note in the information section and the larger transmission amplitude $s_{0} = 2.5 \ \rm V$ compared to the (modified) AMI code, we obtain:

$$P_{\rm S,\,MMS43} = \frac{2}{3} \cdot \frac{{s_0}^2}{R} = \frac{2}{3} \cdot \frac{({2.5\,{\rm V}})^2}{100\,{\rm \Omega}} \hspace{0.15cm}\underline{\approx 4.2\,{\rm mW}} \hspace{0.05cm}.$$

@@ Line 59: / Line 59: @@
 $R_{\rm U_{K0}} \ = \ $ { 120000 3% } $\ \rm ternary \ symbols/second$
-{Es gelte&nbsp; $s_{0} = 2.5 \hspace{0.1cm} {\rm V}$&nbsp; und&nbsp; $R = 100 \hspace{0.1cm} {\rm \Omega }$. Wie groß ist die Sendeleistung? <br>''Hinweis:'' &nbsp; Gehen Sie vereinfachend von gleichwahrscheinlichen Ternärsymbolen aus.
+{Let&nbsp; $s_{0} = 2.5 \hspace{0.1cm} {\rm V}$&nbsp; and&nbsp; $R = 100 \hspace{0.1cm} {\rm \Omega }$ be valid. What is the transmit power? <br>''Note:'' &nbsp; For simplicity, assume equally probable ternary symbols.
 |type="{}"}
 $P_{\rm S,\ MMS43} \ = \ $ { 4.2 3% } $\ \rm mW$
 </quiz>
-===Musterlösung===
+===Solution===
 {{ML-Kopf}}
-'''(1)'''&nbsp; Richtig sind <u>die zwei ersten Aussagen</u>:
+'''(1)'''&nbsp; <u>The first two statements</u> are correct:
-*Der modifizierte AMI–Code ist ein so genannter Pseudo–Ternärcode mit $T_{\rm S} = T_{\rm B}$ und symbolweiser Codierung.
+*The modified AMI code is a so-called pseudo-ternary code with $T_{\rm S} = T_{\rm B}$ and symbol-wise coding.
-*Die angegebenen Zuordnungen gelten für den herkömmlichen AMI–Code.
+*The stated assignments apply to the conventional AMI code.
-*Dagegen wird beim modifizierten AMI–Code die binäre „1” durch den Spannungswert $0 \ \rm V$ repräsentiert und die binäre „0” alternierend durch $+s_{0}$ bzw. $-s_{0}$, wobei für $s_{0} = 0.75 \ \rm V$ zu setzen ist.
+*On the other hand, in the modified AMI code the binary "1" is represented by the voltage value $0 \ \rm V$ and the binary "0" alternately by $+s_{0}$ bzw. $-s_{0}$, where for $s_{0} = 0.75 \ \rm V$ is to be set.
 '''(2)'''&nbsp;
-*Die äquivalente Bitrate des AMI–codierten Signals beträgt $R_{\rm C} = {\rm log_2}\hspace{0.05cm}(3)/T_{\rm S}$; die Bitrate des redundanzfreien binären Quellensignals ist gleich $R_{\rm B} = 1/T_{\rm B}$.
+*The equivalent bit rate of the AMI encoded signal is $R_{\rm C} = {\rm log_2}\hspace{0.05cm}(3)/T_{\rm S}$; the bit rate of the redundancy-free binary source signal is equal to $R_{\rm B} = 1/T_{\rm B}$.
-*Mit $T_{\rm S} = T_{\rm B}$ erhält man entsprechend dem Kapitel [[Digital_Signal_Transmission/Grundlagen_der_codierten_Übertragung|Grundlagen der codierten Übertragung]] des Buches „Digitalsignalübertragung” für die (relative) Redundanz des modifizierten AMI–Codes:
+*With $T_{\rm S} = T_{\rm B}$, according to the chapter [[Digital_Signal_Transmission/Basics_of_Coded_Transmission|"Basics of Coded Transmission"]] of the book "Digital Signal Transmission", we obtain for the (relative) redundancy of the modified AMI code:
 :$$r_{\rm AMI} = \frac{R_{\rm C}-R_{\rm B}}{R_{\rm C}} = 1 - \frac{1}{{\rm ld}\,(3)} \hspace{0.15cm}\underline{\approx 36.9\,\%} \hspace{0.05cm}.$$
 '''(3)'''&nbsp;
-*Unter Verwendung des Einheitswiderstandes $R = 1 \ \rm \Omega $ gilt für die Sendeleistung (mit der Einheit $\rm V^{2}$):
+*Using the unit impedance $R = 1 \ \rm \Omega $, the following applies to the transmit power (with the unit $\rm V^{2}$):
 :$$P_{\rm S,\,AMI} = {1}/{2} \cdot {s_0}^2 = {1}/{2} \cdot {0.75\,{\rm V}}^2 \approx 0.28\,{\rm V^2} \hspace{0.05cm}.$$
-*Hierbei ist berücksichtigt, dass das AMI–codierte Signal in der Hälfte der Zeit gleich $0 \ \rm V$ ist.
+*Here it is considered that the AMI encoded signal is equal to $0 \ \rm V$ in half of the time.
-*Bei Berücksichtigung des Widerstandes $R = 100 \ \rm \Omega$ ergibt sich schließlich:
+*Finally, considering the impedance $R = 100 \ \rm \Omega$, we get:
 :$$P_{\rm S,\,AMI} = \frac{0.28\,{\rm V^2}}{100\,\Omega} \hspace{0.15cm}\underline{ = 2.8\,{\rm mW}} \hspace{0.05cm}.$$
-'''(4)'''&nbsp; Der MMS43–Code arbeitet tatsächlich blockweise, wobei $m_{q} = 4 \ \rm Binärsymbole$ durch  $m_{c} = 3 \ \rm Ternärsymbole$ ersetzt werden:
+'''(4)'''&nbsp; The MMS43 code actually operates in blocks, with $m_{q} = 4 \ \rm binary \ symbols$ replaced by $m_{c} = 3 \ \rm ternary \ symbols$:
 :$$4 \cdot T_{\rm B} = 3 \cdot T_{\rm S}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm S} = {4}/{3} \cdot T_{\rm B} \hspace{0.05cm}.$$
-*Das heißt: Der erste Lösungsvorschlag trifft nicht zu ebenso wie der letzte. Richtig ist nur der  <u>Vorschlag 2</u>:
+*Das heißt: That means: The first solution does not apply as well as the last one. Only <u>solution 2</u> is correct:
-*Bei Blockcodierung kann das Binärsymbol „0” nicht einheitlich durch das gleiche Codesymbol ersetzt werden.
+*In block coding, the binary symbol "0" cannot be uniformly replaced by the same code symbol.
-*Vielmehr lässt sich die Codierung wie folgt beschreiben, wenn man zu Beginn von der laufenden digitalen Summe ${\it \Sigma}_{0} = 0$ ausgeht (siehe Grafik auf der Angabenseite):
+*Rather, the encoding can be described as follows, assuming the running digital sum ${\it \Sigma}_{0} = 0$ at the beginning (see graphic in the information section):
 :$$\mathbf{0 1 0 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{0 + +}\hspace{0.2cm}({\it \Sigma}_1 = 2)\hspace{0.05cm},$$
 :$$ \mathbf{0 1 1 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{- \,0 \,\,+}\hspace{0.2cm}({\it \Sigma}_2 = 2)\hspace{0.05cm},$$
 :$$ \mathbf{0 1 0 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{- \,0\,\,\, 0}\hspace{0.2cm}({\it \Sigma}_3 = 1) \hspace{0.05cm}.$$
-In der [[Aufgaben:Aufgabe_1.4Z:_Modifizierter_MS43–Code|Aufgabe 1.4Z]] wird der MMS43–Code noch ausführlicher behandelt.
+[[Aufgaben:Exercise_1.4Z:_Modified_MS43_Code|"Exercise 1.4Z"]] discusses the MMS43 code in more detail.
-'''(5)'''&nbsp;  Der MMS43–Code gehört zur Klasse der 4B3T–Codes. Für diese gilt:
+'''(5)'''&nbsp; The MMS43 code belongs to the class of 4B3T codes. For these it is valid:
 :$$R_{\rm B} = \frac{1}{T_{\rm B}}, \hspace{0.2cm} R_{\rm C} = \frac{{\rm ld}\,(3)}{T_{\rm S}}\hspace{0.3cm}
 \Rightarrow \hspace{0.3cm}r_{\rm MMS43} = 1 - \frac{R_{\rm B}}{R_{\rm C}} = 1 - \frac{T_{\rm S}/T_{\rm B}}{{\rm ld}\,(3)} = 1 - \frac{4/3}{{\rm log_2}\,(3)} \hspace{0.15cm}\underline{\approx 15.9\,\%} \hspace{0.05cm}.$$
@@ Line 106: / Line 106: @@
-'''(6)'''&nbsp; Pro Millisekunde werden auf dem $\rm U_{K0}$–Bus die folgende Anzahl an Ternärsymbolen übertragen:
+'''(6)'''&nbsp; The following number of ternary symbols are transmitted on the $\rm U_{K0}$ bus per millisecond:
-*Kanal B1: &nbsp;  64 Binärsymbole &nbsp; &rArr; &nbsp;  48 Ternärsymbole,
+*Channel B1: &nbsp;  64 binary symbols &nbsp; &rArr; &nbsp;  48 ternary symbols,
-*Kanal B2: &nbsp;  64 Binärsymbole &nbsp; &rArr; &nbsp;  48 Ternärsymbole,
+*Channel B2: &nbsp;  64 binary symbols &nbsp; &rArr; &nbsp;  48 ternary symbols,
-*D–Kanal: &nbsp;  16 Binärsymbole &nbsp; &rArr; &nbsp;  12 Ternärsymbole,
+*D channel: &nbsp;  16 binary symbols &nbsp; &rArr; &nbsp;  12 ternary symbols,
-*Synchronisations– und Steuersymbole &nbsp; &rArr; &nbsp;  12 Ternärsymbole.
+*Synchronization and control symbols &nbsp; &rArr; &nbsp;  12 ternary symbols.
-Dies ergibt als Summe 120 Ternärsymbole pro Millisekunde bzw. <u>120 000  Ternärsymbole pro Sekunde</u>.
+As a sum, this results in 120 ternary symbols per millisecond or <u>120,000 ternary symbols per second</u>.
-'''(7)'''&nbsp; Unter Berücksichtigung des Hinweises auf der Angabenseite und der gegenüber dem (modifizierten) AMI–Code größeren Sendeamplitude $s_{0} = 2.5 \ \rm V$ erhält man:
+'''(7)'''&nbsp; Considering the note in the information section and the larger transmission amplitude $s_{0} = 2.5 \ \rm V$ compared to the (modified) AMI code, we obtain:
 :$$P_{\rm S,\,MMS43} = \frac{2}{3} \cdot \frac{{s_0}^2}{R} = \frac{2}{3} \cdot \frac{({2.5\,{\rm V}})^2}{100\,{\rm \Omega}} \hspace{0.15cm}\underline{\approx 4.2\,{\rm mW}} \hspace{0.05cm}.$$