Difference between revisions of "Aufgaben:Exercise 4.09: Recursive Systematic Convolutional Codes"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/The_Basics_of_Turbo_Codes}} |
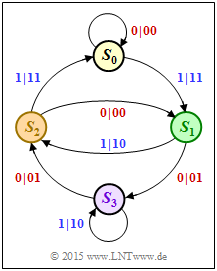
| − | [[File:P_ID3040__KC_A_4_9_v1.png|right|frame| | + | [[File:P_ID3040__KC_A_4_9_v1.png|right|frame|State transition diagram of an RSC code]] |
| − | In | + | In the [[Aufgaben:Exercise_4.08:_Repetition_to_the_Convolutional_Codes|"Exercise 4.8"]] important properties of convolutional codes have already been derived from the state transition diagram, assuming a non-recursive filter structure. |
| − | + | Now a rate $1/2$ RSC code is treated in a similar manner. Here "RSC" stands for "Recursive Systematic Convolutional". | |
| − | + | The transfer function matrix of an RSC convolutional code can be specified as follows: | |
:$${\boldsymbol{\rm G}}(D) = \left [ 1\hspace{0.05cm},\hspace{0.3cm} G^{(2)}(D)/G^{(1)}(D) \right ] | :$${\boldsymbol{\rm G}}(D) = \left [ 1\hspace{0.05cm},\hspace{0.3cm} G^{(2)}(D)/G^{(1)}(D) \right ] | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Otherwise, exactly the same conditions apply here as in exercise 4.8. We refer again to the following theory pages: | |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Algebraic_and_Polynomial_Description#Systematic_convolutional_codes|"Systematic convolutional codes"]] |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Representation_in_the_state_transition_diagram|"Representation in the state transition diagram"]] |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Definition_of_the_free_distance|"Definition of the free distance"]] |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Algebraic_and_Polynomial_Description#GF.282.29_description_forms_of_a_digital_filter|"GF(2) description forms of a digital filter"]] |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Algebraic_and_Polynomial_Description#Application_of_the_D.E2.80.93transform_to_rate_.7F.27.22.60UNIQ-MathJax160-QINU.60.22.27.7F_convolution_encoders| "Application of the D–transform to rate 1/n convolution encoders"]] |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Algebraic_and_Polynomial_Description#Filter_structure_with_fractional.E2.80.93rational_transfer_function|"Filter structure with fractional–rational transfer function"]] |
| − | + | In the state transition diagram, the state $S_0$ is always assumed. Two arrows go from each state. The label is "$u_i \hspace{0.05cm}| \hspace{0.05cm} x_i^{(1)}x_i^{(2)}$". For a systematic code, this involves: | |
| − | * | + | * The first code bit is identical to the information bit: $\hspace{0.2cm} x_i^{(1)} = u_i ∈ \{0, \, 1\}$. |
| − | * | + | * The second code bit is the parity-check bit: $\hspace{0.2cm} x_i^{(2)} = p_i ∈ \{0, \, 1\}$. |
| Line 30: | Line 30: | ||
| − | + | Hints: | |
| − | * | + | * The exercise refers to the chapter [[Channel_Coding/The_Basics_of_Turbo_Codes|"Basics of Turbo Codes"]]. |
| − | * | + | * Similar exercises can be found in chapters 3.1 through 3.3. |
| − | * | + | * The following vectorial quantities are used in the questions for this exercise: |
| − | ** | + | ** the information sequence: $\hspace{0.2cm} \underline{u} = (u_1, \, u_2, \text{...} \hspace{0.05cm} )$, |
| − | ** | + | ** the parity-check sequence: $\hspace{0.2cm} \underline{p} = (p_1, \, p_2, \text{...} \hspace{0.05cm})$, |
| − | ** | + | ** the impulse response: $\hspace{0.2cm} \underline{g} = (g_1, \, g_2, \text{...} \hspace{0.05cm} ); \hspace{0.2cm}$ this is equal to the parity sequence $\underline{p}$ for $\underline{u} = (1, \, 0, \, 0, \text{...} \hspace{0.05cm} )$. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
{Wie lautet die Impulsantwort $\underline{g}$ ? | {Wie lautet die Impulsantwort $\underline{g}$ ? | ||
Revision as of 19:42, 29 November 2022
In the "Exercise 4.8" important properties of convolutional codes have already been derived from the state transition diagram, assuming a non-recursive filter structure.
Now a rate $1/2$ RSC code is treated in a similar manner. Here "RSC" stands for "Recursive Systematic Convolutional".
The transfer function matrix of an RSC convolutional code can be specified as follows:
- $${\boldsymbol{\rm G}}(D) = \left [ 1\hspace{0.05cm},\hspace{0.3cm} G^{(2)}(D)/G^{(1)}(D) \right ] \hspace{0.05cm}.$$
Otherwise, exactly the same conditions apply here as in exercise 4.8. We refer again to the following theory pages:
- "Systematic convolutional codes"
- "Representation in the state transition diagram"
- "Definition of the free distance"
- "GF(2) description forms of a digital filter"
- "Application of the D–transform to rate 1/n convolution encoders"
- "Filter structure with fractional–rational transfer function"
In the state transition diagram, the state $S_0$ is always assumed. Two arrows go from each state. The label is "$u_i \hspace{0.05cm}| \hspace{0.05cm} x_i^{(1)}x_i^{(2)}$". For a systematic code, this involves:
- The first code bit is identical to the information bit: $\hspace{0.2cm} x_i^{(1)} = u_i ∈ \{0, \, 1\}$.
- The second code bit is the parity-check bit: $\hspace{0.2cm} x_i^{(2)} = p_i ∈ \{0, \, 1\}$.
Hints:
- The exercise refers to the chapter "Basics of Turbo Codes".
- Similar exercises can be found in chapters 3.1 through 3.3.
- The following vectorial quantities are used in the questions for this exercise:
- the information sequence: $\hspace{0.2cm} \underline{u} = (u_1, \, u_2, \text{...} \hspace{0.05cm} )$,
- the parity-check sequence: $\hspace{0.2cm} \underline{p} = (p_1, \, p_2, \text{...} \hspace{0.05cm})$,
- the impulse response: $\hspace{0.2cm} \underline{g} = (g_1, \, g_2, \text{...} \hspace{0.05cm} ); \hspace{0.2cm}$ this is equal to the parity sequence $\underline{p}$ for $\underline{u} = (1, \, 0, \, 0, \text{...} \hspace{0.05cm} )$.
Questions
Musterlösung
- $$S_0 → S_1 → S_3 → S_2 → S_1 → S_3 → S_2 → S_1 → S_3 → \hspace{0.05cm}\text{...} \hspace{0.05cm}$$
- Bei jedem Übergang ist das erste Codesymbol $x_i^{(1)}$ gleich dem Informationsbit $u_i$ und das Codesymbol $x_i^{(2)}$ gibt das Paritybit $p_i$ an.
- Damit erhält man das Ergebnis entsprechend dem Lösungsvorschlag 1:
- $$\underline{p}= (\hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\text{...} \hspace{0.05cm}) = \underline{g}\hspace{0.05cm}.$$
- Bei einem jeden RSC–Code ist die Impulsantwort $\underline{g}$ unendlich lang und wird irgendwann periodisch, in diesem Beispiel mit der Periode $P = 3$ und "$0, \, 1, \, 1$".
(2) Die Grafik zeigt die Lösung dieser Aufgabe entsprechend der Gleichung $\underline{p} = \underline{u}^{\rm T} \cdot \mathbf{G}$.
- Hierbei ist die Generatormatrix $\mathbf{G}$ nach unten und rechts unendlich weit ausgedehnt.
- Richtig ist der Lösungsvorschlag 2.
(3) Richtig sind die Lösungsvorschläge 1 und 2:
- Zwischen der Impulsantwort $\underline{g}$ und der $D$–Übertragungsfunktion $\mathbf{G}(D)$ besteht der Zusammenhang gemäß dem ersten Lösungsvorschlag:
- $$\underline{g}= (\hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}0\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}0\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, ... ) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1\hspace{-0.05cm}+\hspace{-0.05cm} D\hspace{-0.05cm} +\hspace{-0.05cm} D^2\hspace{-0.05cm} +\hspace{-0.05cm} D^4 \hspace{-0.05cm}+\hspace{-0.05cm} D^5 \hspace{-0.05cm}+\hspace{-0.05cm} D^7 \hspace{-0.05cm}+\hspace{-0.05cm} D^8 + \hspace{0.05cm} \text{...} \hspace{0.05cm}.$$
- Überprüfen wir nun den zweiten Vorschlag:
- $$G(D) = \frac{1+ D^2}{1+ D + D^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G(D) \cdot [1+ D + D^2] = 1+ D^2 \hspace{0.05cm}.$$
- Die folgende Rechnung zeigt, dass diese Gleichung tatsächlich stimmt:
- $$(1+ D+ D^2+ D^4 +D^5 + D^7 + D^8 + \hspace{0.05cm} \text{...}) \cdot (1+ D+ D^2 ) =$$
- $$=1+ D+ D^2\hspace{1.05cm} +D^4 + D^5 \hspace{1.05cm} +D^7 + D^8 \hspace{1.05cm} + D^{10}+ \hspace{0.05cm} \text{...}$$
- $$+ \hspace{0.8cm}D+ D^2+D^3 \hspace{1.05cm}+ D^5 + D^6 \hspace{1.05cm} +D^8 + D^9 \hspace{1.25cm} +\hspace{0.05cm} \text{...} $$
- $$+ \hspace{1.63cm} D^2+D^3+ D^4 \hspace{1.05cm}+ D^6 +D^7 \hspace{1.05cm}+ D^9 + D^{10} \hspace{0.12cm}+ \hspace{0.05cm} \text{...}$$
- $$=\underline{1\hspace{0.72 cm}+ D^2} \hspace{0.05cm}.$$
- Da aber die Gleichung (2) stimmt, muss die letzte Gleichung falsch sein.
(4) Richtig ist nur der Lösungsvorschlag 1:
- Aus $\underline{u} = (1, \, 1, \, 1)$ folgt $U(D) = 1 + D + D^2$. Damit gilt auch:
- $$P(D) = U(D) \cdot G(D) = (1+D+D^2) \cdot \frac{1+D^2}{1+D+D^2}= 1+D^2\hspace{0.3cm} \Rightarrow\hspace{0.3cm} \underline{p}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm})\hspace{0.05cm}. $$
- Wären die Größen $u_i$ und $g_i$ reellwertig, so würde die (diskrete) Faltung $\underline{p} = \underline{u} * \underline{g}$ stets zu einer Verbreiterung führen ⇒ $\underline{p}$ wäre in diesem Fall breiter als $\underline{u}$ und auch breiter als $\underline{g}$.
- Bei $u_i ∈ {\rm GF}(2)$ und $g_i ∈ {\rm GF}(2)$ kann es (muss es aber nicht) dagegen vorkommen, dass auch bei unbegrenztem $\underline{u}$ oder bei unbegrenztem $\underline{g}$ das Faltungsprodukt $\underline{p} = \underline{u} * \underline{g}$ begrenzt ist.
- Das Ergebnis wird abschließend noch entsprechend der Gleichung $\underline{p} = \underline{u}^{\rm T} \cdot \mathbf{G}$ überprüft.
(5) Nach ähnlicher Vorgehensweise wie in der Aufgabe A4.8, (4) erkennt man:
- Die freie Distanz wird auch hier durch den Pfad $S_0 → S_0 → S_1 → S_2 → S_0 → S_0 → \hspace{0.05cm}\text{...}\hspace{0.05cm}$ bestimmt.
- Die zugehörige Codesequenz $\underline{x}$ ist nun aber " $00 \ 11 \ 10 \ 11 \ 00 \ ... $".
- Damit ergibt sich die freie Distanz zu $d_{\rm F} \ \underline{= 5}$.
- Beim nichtrekursiven Code (Aufgabe 4.8) war dagegen die freie Distanz $d_{\rm F} = 3$.