Difference between revisions of "Aufgaben:Exercise 3.7: Comparison of Two Convolutional Encoders"
From LNTwww
| Line 20: | Line 20: | ||
| − | + | <u>Hints:</u> | |
| − | |||
| − | Hints: | ||
*This exercise belongs to the chapter [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram| "Code description with state and trellis diagram"]]. | *This exercise belongs to the chapter [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram| "Code description with state and trellis diagram"]]. | ||
| Line 56: | Line 54: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
[[File:P_ID2673__KC_A_3_7a_neu.png|right|frame|Calculation of the code sequence]] | [[File:P_ID2673__KC_A_3_7a_neu.png|right|frame|Calculation of the code sequence]] | ||
| − | '''(1)''' The calculation is based on the equations | + | '''(1)''' The calculation is based on the equations |
:$$x_i^{(1)} = u_i + u_{i–2},$$ | :$$x_i^{(1)} = u_i + u_{i–2},$$ | ||
:$$x_i^{(2)} = u_i + u_{i–1} + u_{i–2}.$$ | :$$x_i^{(2)} = u_i + u_{i–1} + u_{i–2}.$$ | ||
| − | *Initially, the two memories ( | + | *Initially, the two memories $(u_{i–1}$ and $u_{i–2})$ are preallocated with zeros ⇒ $s_1 = S_0$. |
| − | *With $u_1 = 0$, we get $\underline{x}_1 = (00)$ and $s_2 = S_0$. | + | |
| − | *With $u_2 = 1$ one obtains the output $\underline{x}_2 = (11)$ and the new state $s_3 = S_3$. | + | *With $u_1 = 0$, we get $\underline{x}_1 = (00)$ and $s_2 = S_0$. |
| + | |||
| + | *With $u_2 = 1$, one obtains the output $\underline{x}_2 = (11)$ and the new state $s_3 = S_3$. | ||
| − | From the adjacent calculation scheme one recognizes the correctness of the <u>proposed solutions 1 and 4</u>. | + | From the adjacent calculation scheme one recognizes the correctness of the <u>proposed solutions 1 and 4</u>. |
[[File:P_ID2674__KC_A_3_7b.png|right|frame|State transition diagram of encoder $\rm A$]] | [[File:P_ID2674__KC_A_3_7b.png|right|frame|State transition diagram of encoder $\rm A$]] | ||
| − | '''(2)''' <u>All proposed solutions</u> are correct: | + | '''(2)''' <u>All proposed solutions</u> are correct: |
| − | *This can be seen by evaluating the table at '''(1)'''. | + | *This can be seen by evaluating the table at subtask '''(1)'''. |
| + | |||
*The results are shown in the adjacent graph. | *The results are shown in the adjacent graph. | ||
<br clear=all> | <br clear=all> | ||
[[File:P_ID2675__KC_A_3_7c.png|right|frame|State transition diagram of encoder $\rm B$]] | [[File:P_ID2675__KC_A_3_7c.png|right|frame|State transition diagram of encoder $\rm B$]] | ||
| − | '''(3)''' Correct is only <u>statement 3</u>: | + | '''(3)''' Correct is only <u>statement 3</u>: |
| − | *The state transition diagram of | + | *The state transition diagram of encoder $\rm B$ is sketched on the right. For derivation and interpretation, see section [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Representation_in_the_state_transition_diagram|"Representation in the state transition diagram"]]. |
| − | *If we swap the two output bits $x_i^{(1)}$ and $x_i^{(2)}$, we get from the convolutional encoder $\rm A$ to the convolutional encoder $\rm B$ (and vice versa). | + | |
| + | *If we swap the two output bits $x_i^{(1)}$ and $x_i^{(2)}$, we get from the convolutional encoder $\rm A$ to the convolutional encoder $\rm B$ $($and vice versa$)$. | ||
Revision as of 16:03, 14 November 2022
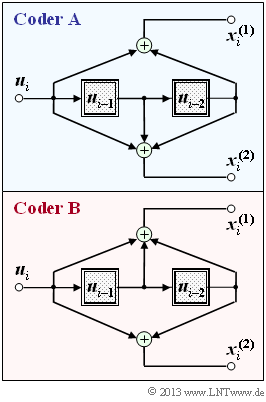
The graph shows two rate $1/2$ convolutional encoders, each with memory $m = 2$:
- The encoder $\rm A$ has the transfer function matrix $\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$.
- In encoder $\rm B$ the two filters $($top and bottom$)$ are interchanged, and it holds:
- $$\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2).$$
The lower encoder $\rm B$ has already been treated in detail in the theory part.
In the present exercise,
- you are first to determine the state transition diagram for encoder $\rm A$,
- and then work out the differences and the similarities between the two state diagrams.
Hints:
- This exercise belongs to the chapter "Code description with state and trellis diagram".
- Reference is made in particular to the sections
Questions
Solution
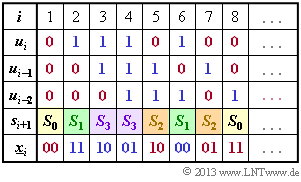
(1) The calculation is based on the equations
- $$x_i^{(1)} = u_i + u_{i–2},$$
- $$x_i^{(2)} = u_i + u_{i–1} + u_{i–2}.$$
- Initially, the two memories $(u_{i–1}$ and $u_{i–2})$ are preallocated with zeros ⇒ $s_1 = S_0$.
- With $u_1 = 0$, we get $\underline{x}_1 = (00)$ and $s_2 = S_0$.
- With $u_2 = 1$, one obtains the output $\underline{x}_2 = (11)$ and the new state $s_3 = S_3$.
From the adjacent calculation scheme one recognizes the correctness of the proposed solutions 1 and 4.
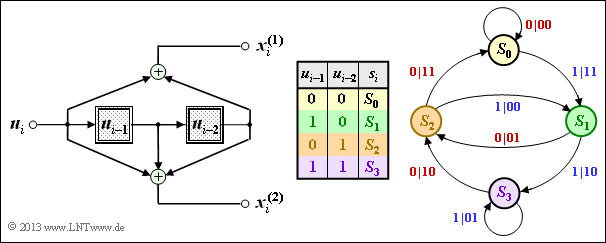
(2) All proposed solutions are correct:
- This can be seen by evaluating the table at subtask (1).
- The results are shown in the adjacent graph.
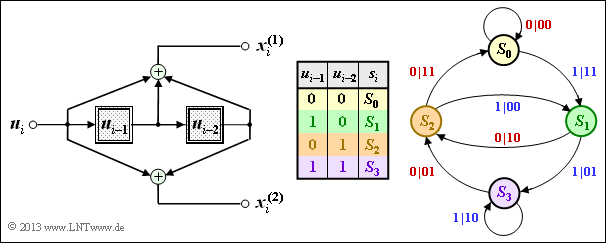
(3) Correct is only statement 3:
- The state transition diagram of encoder $\rm B$ is sketched on the right. For derivation and interpretation, see section "Representation in the state transition diagram".
- If we swap the two output bits $x_i^{(1)}$ and $x_i^{(2)}$, we get from the convolutional encoder $\rm A$ to the convolutional encoder $\rm B$ $($and vice versa$)$.