Difference between revisions of "Aufgaben:Exercise 4.08: Repetition to the Convolutional Codes"
| Line 16: | Line 16: | ||
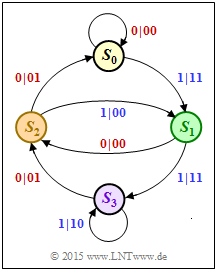
In the state transition diagram, the state $S_0$ is always assumed. Two arrows go from each state. The label is "$u_i \hspace{0.05cm}|\hspace{0.05cm} x_i^{(1)}x_i^{(2)}$". For a systematic code, this holds: | In the state transition diagram, the state $S_0$ is always assumed. Two arrows go from each state. The label is "$u_i \hspace{0.05cm}|\hspace{0.05cm} x_i^{(1)}x_i^{(2)}$". For a systematic code, this holds: | ||
* The first code bit is identical to the information bit: $\ x_i^{(1)} = u_i ∈ \{0, \, 1\}$ | * The first code bit is identical to the information bit: $\ x_i^{(1)} = u_i ∈ \{0, \, 1\}$ | ||
| − | * The second code bit is the check bit | + | * The second code bit is the parity-check bit: $\ x_i^{(2)} = p_i ∈ \{0, \, 1\}$. |
| Line 28: | Line 28: | ||
* The following semi–infinite vectors are used in the questions for this exercise: | * The following semi–infinite vectors are used in the questions for this exercise: | ||
:* information sequence $\ \underline{u} = (u_1, \, u_2, \text{ ...})$, | :* information sequence $\ \underline{u} = (u_1, \, u_2, \text{ ...})$, | ||
| − | :* parity sequence $\ \underline{p} = (p_1, \, p_2, \text{ ...})$, | + | :* parity-check sequence $\ \underline{p} = (p_1, \, p_2, \text{ ...})$, |
| − | :* impulse response $\ \underline{g} = (g_1, \, g_2, \text{ ...})$; this is equal to the parity sequence $\underline{p}$ for $\underline{u} = (1, \, 0, \, 0, \text{ ...})$. | + | :* impulse response $\ \underline{g} = (g_1, \, g_2, \text{ ...})$; this is equal to the parity-check sequence $\underline{p}$ for $\underline{u} = (1, \, 0, \, 0, \text{ ...})$. |
| Line 41: | Line 41: | ||
+ $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \text{ ...})$ holds. | + $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \text{ ...})$ holds. | ||
| − | {Now let $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ with $u_7 ∈ \{0, \, 1\}$. Which statements are true for the parity sequence $\underline{p}$ ? | + | {Now let $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ with $u_7 ∈ \{0, \, 1\}$. Which statements are true for the parity-check sequence $\underline{p}$ ? |
|type="[]"} | |type="[]"} | ||
| − | + The first six bits of the parity sequence are "$1, \, 0, \, 1, \, 1, \, 0, \, 1$". | + | + The first six bits of the parity-check sequence are "$1, \, 0, \, 1, \, 1, \, 0, \, 1$". |
+ With $u_7 = 0$ holds $p_i = 0$ for $i > 6$. | + With $u_7 = 0$ holds $p_i = 0$ for $i > 6$. | ||
- With $u_7 = 1$ holds $p_i = 0$ for $i > 8$. | - With $u_7 = 1$ holds $p_i = 0$ for $i > 8$. | ||
| Line 53: | Line 53: | ||
- It holds $\mathbf{G}(D) = \big [1 + D^2 \big ]$. | - It holds $\mathbf{G}(D) = \big [1 + D^2 \big ]$. | ||
| − | {Now consider the bounded input sequence $\underline{u} = (1, \, 0, \, 1, \, 0, \, 0, \, 1)$. Which statements hold for the then also bounded parity sequence $\underline{p}$? | + | {Now consider the bounded input sequence $\underline{u} = (1, \, 0, \, 1, \, 0, \, 0, \, 1)$. Which statements hold for the then also bounded parity-check sequence $\underline{p}$? |
|type="[]"} | |type="[]"} | ||
| − | - The first eight bits of the parity sequence are "$1, \, 0, \, 1, \, 1, \, 1, \, 0, \, 1, \, 0$." | + | - The first eight bits of the parity-check sequence are "$1, \, 0, \, 1, \, 1, \, 1, \, 0, \, 1, \, 0$." |
| − | + The first eight bits of the parity sequence are "$1, \, 0, \, 0, \, 0, \, 1, \, 1, \, 0, \, 1$". | + | + The first eight bits of the parity-check sequence are "$1, \, 0, \, 0, \, 0, \, 1, \, 1, \, 0, \, 1$". |
+ It holds $p_i = 0$ for $i ≥ 9$. | + It holds $p_i = 0$ for $i ≥ 9$. | ||
| Line 75: | Line 75: | ||
| − | '''(2)''' Let $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ and $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$. Then the following holds for the parity sequence due to linearity: | + | '''(2)''' Let $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ and $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$. Then the following holds for the parity-check sequence due to linearity: |
:$$\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | :$$\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | ||
(\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm} 0,\hspace{0.05cm} u_7\hspace{0.05cm} ) | (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm} 0,\hspace{0.05cm} u_7\hspace{0.05cm} ) | ||
Revision as of 19:44, 29 November 2022
The turbo codes are based on convolutional codes, which are discussed in detail in the chapter "Basics of Convolutional Coding" .
Starting from the adjacent state transition diagram, essential properties and characteristics of the considered rate $1/2$ convolutional code shall be determined, and we explicitly refer to the following theory pages:
- "Systematic convolutional codes"
- "Representation in the state transition diagram"
- "Definition of the free distance"
- "GF(2) description forms of a digital filter"
- "Application of $D$–transform to rate 1/n convolutional codes."
In the state transition diagram, the state $S_0$ is always assumed. Two arrows go from each state. The label is "$u_i \hspace{0.05cm}|\hspace{0.05cm} x_i^{(1)}x_i^{(2)}$". For a systematic code, this holds:
- The first code bit is identical to the information bit: $\ x_i^{(1)} = u_i ∈ \{0, \, 1\}$
- The second code bit is the parity-check bit: $\ x_i^{(2)} = p_i ∈ \{0, \, 1\}$.
Hints:
- The exercise refers to the chapter "Basics of Turbo Codes".
- The following semi–infinite vectors are used in the questions for this exercise:
- information sequence $\ \underline{u} = (u_1, \, u_2, \text{ ...})$,
- parity-check sequence $\ \underline{p} = (p_1, \, p_2, \text{ ...})$,
- impulse response $\ \underline{g} = (g_1, \, g_2, \text{ ...})$; this is equal to the parity-check sequence $\underline{p}$ for $\underline{u} = (1, \, 0, \, 0, \text{ ...})$.
Questions
Solution
- The impulse response $\underline{g}$ is equal to the output sequence $\underline{p}$ for the input sequence $\underline{u} = (1, \, 0, \, 0, \, 0, \text{ ...})$.
- Based on the state $S_0$, the state transition diagram results in the following transitions:
- $$S_0 → S_1 → S_2 → S_0 → S_0 → S_0 → \text{ ...} \hspace{0.6cm} \Rightarrow \hspace{0.5cm} {\rm impulse\:response} \text{:} \hspace{0.2cm} \underline{g} = (1, \, 0, \, 1, \, 0, \, 0) \, .$$
- For a non-recursive filter with memory $m$, $g_i ≡ 0$ holds for $i > m$. In our example, $m = 2$.
- In contrast, the proposed solution 1 applies to the recursive filter (RSC) corresponding to "Exercise 4.9".
(2) Let $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ and $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$. Then the following holds for the parity-check sequence due to linearity:
- $$\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm} 0,\hspace{0.05cm} u_7\hspace{0.05cm} ) * (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0 ,\hspace{0.05cm} 0,\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{ ...})= $$
- $$\ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm}0, \hspace{0.05cm} \text{ ...} \hspace{0.05cm})\hspace{0.05cm}\oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm}0, \hspace{0.05cm} \text{ ...}\hspace{0.05cm})\hspace{0.05cm}\oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} u_7,\hspace{0.05cm} 0,\hspace{0.05cm}u_7, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) $$
- $$\Rightarrow \hspace{0.3cm}\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} u_7,\hspace{0.05cm} 0,\hspace{0.05cm}u_7, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) \hspace{0.05cm}.$$
Correct are therefore the proposed solutions 1 and 2 in contrast to the answer 3:
- For $u_7 = 1$ gilt $p_7 = 1, \ p_8 = 0, \ p_9 = 1$ and $p_i ≡ 0$ for $i > 9$.
(3) Correct is the proposed solution 2:
- From the state transition diagram one can see the code parameters $k = 1$ and $n = 2$.
- This means: the transfer function matrix $\mathbf{G}(D)$ consists of two elements ⇒ the proposition 3 is wrong.
- The first component of $\mathbf{G}(D)$ is actually 1, since there is a systematic code: $\ \underline{x}^{(1)} ≡ \underline{z}$.
- The second component of $\mathbf{G}(D)$ is equal to the $D$–transform of the impulse response $\underline{g}$, where the dummy–variable $D$ indicates a delay of one bit:
- $$\underline{g}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{ ...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G^{(2)}(D) = 1+ D^2\hspace{0.05cm}. $$
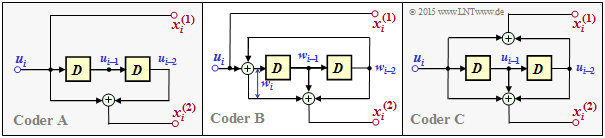
Going beyond the question, we also consider here the filter structure at hand:
In the diagram, the encoder considered here is shown as coder $\rm A$ on the left.
- This is systematic like the encoder $\rm B$, and
- but, unlike coder $\rm B$, is based on a non-recursive filter.
- The coder $\rm C$ also has a nonrecursive structure, but is not systematic.
- The equivalent systematic representation of encoder $\rm C$ is encoder $\rm B$.
(4) Correct are the proposed solutions 2 and 3:
- The exercise could be solved in the same way as subtask (2).
- However, we choose here for a change the way about the $D$–transform:
- $$\underline{u}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = 1+ D^2 + D^5$$
- $$\Rightarrow \hspace{0.3cm} P(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} U(D) \cdot G(D) = (1+ D^2 + D^5) \cdot (1+ D^2 ) =1+ D^2 + D^5 + D^2 + D^4 + D^7 = 1+ D^4 + D^5 + D^7$$
- $$\Rightarrow \hspace{0.3cm} \underline{p}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm})\hspace{0.05cm}.$$
(5) The free distance $d_{\rm F}$ of a convolutional encoder is equal to the minimum number of bits by which any two sequences of this code differ.
- If we take as a reference the zero sequence, as is commonly done $\underline{0} \ \Rightarrow \ S_0 → S_0 → S_0 → S_0 → \ \text{ ...} \ $ off, then $d_{\rm F}$ is simultaneously obtained as the minimum Hamming weight (number of ones) of an admissible code sequence $\underline{x} ≠ \underline{0}$.
- From the state transition diagram, we can see that the free distance for example is given by the path.
- $$ S_0 → S_0 → S_1 → S_2 → S_0 → S_0 → \text{ ...}$$
- thus identified by the code sequence $00 \hspace{0.1cm} 11 \hspace{0.1cm} 00 \hspace{0.1cm} 01 \hspace{0.1cm} 00 \text{ ...} \ .$
- Accordingly, for the free distance of this non-recursive code, $\hspace{0.2cm} d_{\rm F} \ \underline{= 3}$.