Difference between revisions of "Digital Signal Transmission/Redundancy-Free Coding"
| Line 243: | Line 243: | ||
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
<br> | <br> | ||
| − | [[Aufgaben:2. | + | [[Aufgaben:2.3_Binärsignal_und_Quaternärsignal|Aufgabe 2.3: Binärsignal und Quaternärsignal]] |
| − | [[Aufgaben:2. | + | [[Aufgaben:2.4_Dualcodierung_und_Graycodierung|Aufgabe 2.4: Dualcodierung und Graycodierung]] |
| − | [[ | + | [[Aufgaben:2.4Z_Fehlerwahrscheinlichkeiten_beim_Oktalsystem|Aufgabe 2.4Z: Fehlerwahrscheinlichkeiten beim Oktalsystem]] |
| − | [[Aufgaben:2. | + | [[Aufgaben:2.5_Ternäre_Signalübertragung|Aufgabe 2.5: Ternäre Signalübertragung]] |
{{Display}} | {{Display}} | ||
Revision as of 11:36, 17 November 2017
Contents
- 1 Blockweise Codierung vs. symbolweise Codierung
- 2 Quaternärsignal mit rc = 0 und Ternärsignal mit rc ≈ 0
- 3 AKF und LDS eines Mehrstufensignals
- 4 Fehlerwahrscheinlichkeit eines Mehrstufensystems
- 5 Vergleich zwischen Binärsystem und Mehrstufensystem
- 6 Symbol– und Bitfehlerwahrscheinlichkeit
- 7 Aufgaben zum Kapitel
Blockweise Codierung vs. symbolweise Codierung
Bei der Übertragungscodierung unterscheidet man zwischen zwei Arten, der symbolweisen und der blockweisen Codierung.
Bei symbolweiser Codierung, die im Kapitel Symbolweise Codierung mit Pseudoternärcodes im Detail beschrieben ist, wird mit jedem ankommenden Quellensymbol $q_\nu$ ein Codesymbol $c_\nu$ erzeugt, das außer vom aktuellen Symbol auch von vorangegangenen Symbolen $q_{\nu -1}$, $q_{\nu -2}$, ... abhängen kann.
- Typisch für alle Übertragungscodes zur symbolweisen Codierung ist, dass die Symboldauer $T_c$ des meist mehrstufigen und redundanten Codersignals $c(t)$ mit der Bitdauer $T_q$ der als binär und redundanzfrei angenommenen Nachrichtenquelle übereinstimmt.
Dagegen wird bei der blockweisen Codierung jeweils einem Block von $m_q$ binären Quellensymbolen $(M_q = 2)$ der Bitdauer $T_q$ eine ein–eindeutige Sequenz von $m_c$ Codesymbolen aus einem Alphabet mit dem Codesymbolumfang $M_c \ge 2$ zugeordnet.
- Für die Symboldauer eines Codesymbols gilt dann:
- $$T_c = \frac{m_q}{m_c} \cdot T_q \hspace{0.05cm},$$
- Die relative Redundanz eines Blockcodes beträgt allgemein
- $$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.05cm}.$$
Genauere Angaben zu den Blockcodes finden Sie im Kapitel Blockweise Codierung mit 4B3T-Codes.
$\text{Beispiel 1:}$ Bei den Pseudoternärcodes wird durch die Erhöhung der Stufenzahl von $M_q = 2$ auf $M_c = 3$ bei gleicher Symboldauer $(T_c = T_q)$ eine relative Redundanz von $r_c = 1 - 1/\log_2 \hspace{0.05cm} (3) \approx 37\%$ hinzugefügt.
Im Gegensatz dazu arbeiten die so genannten 4B3T–Codes auf Blockebene mit den Codeparametern $m_q = 4$, $M_q = 2$, $m_c = 3$ und $M_c = 3$ und besitzen eine relative Redundanz von ca. $16\%$. Das Sendesignal $s(t)$ ist hier wegen ${T_c}/{T_q} = 4/3$ niederfrequenter als bei uncodierter Übertragung, was die teuere Bandbreite verringert und zudem für viele Nachrichtenkanäle auch aus übertragungstechnischer Sicht von Vorteil ist.
Quaternärsignal mit rc = 0 und Ternärsignal mit rc ≈ 0
Ein Sonderfall eines Blockcodes ist die redundanzfreie Codierung. Ausgehend vom redundanzfreien binären Quellensignal $q(t)$ mit Bitdauer $T_q$ wird ein $M_c$–stufiges Codersignal $C(t)$ generiert, wobei die Symboldauer $T_c = T_q \cdot \log_2 \hspace{0.05cm} (M_c)$. Somit ergibt sich für die relative Redundanz:
- $$r_c = 1- \frac{T_c}{T_q \cdot {\rm log_2}\hspace{0.05cm} (M_c)} = 1- \frac{m_q}{m_c \cdot {\rm log_2} \hspace{0.05cm}(M_c)}= 0 \hspace{0.05cm}.$$
Dabei gilt:
- Ist $M_c$ eine Potenz zur Basis $2$, so werden $m_q = \log_2 \hspace{0.05cm} (M_c)$ zu einem einzigen Codesymbol $(m_c = 1)$ zusammengefasst. In diesem Fall ist die relative Redundanz tatsächlich $r_c = 0$.
- Ist $M_c$ keine Zweierpotenz, so ist eine hundertprozentig redundanzfreie Blockcodierung nicht möglich. Codiert man beispielweise $m_q = 3$ Binärsymbole durch $m_c = 2$ Ternärsymbole und setzt $T_c = 1.5 \cdot T_q$, so verbleibt eine relative Redundanz von $r_c = 1-1.5/ \log_2 \hspace{0.05cm} (3) \approx 5\%$.
- Codiert man einen Block von $128$ Binärsymbolen mit $81$ Ternärsymbolen, so ergibt sich eine relative Coderedundanz von weniger als $r_c = 0.3\%$.
Zur Vereinfachung der Schreibweise und zur Nomenklaturanpassung an das erste Hauptkapitel verwenden wir im Folgenden
- die Bitdauer $T_{\rm B} = T_q$ des redundanzfreien binären Quellensignals,
- die Symboldauer $T = T_c$ von Codersignal und Sendesignal, sowie
- die Stufenzahl $M = M_c$.
Damit ergibt sich für das Sendesignal die identische Form wie bei der Binärübertragung, jedoch mit anderen Amplitudenkoeffizienten:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.3cm}{\rm mit}\hspace{0.3cm} a_\nu \in \{ a_1, \text{...} , a_\mu , \text{...} , a_{ M}\}\hspace{0.05cm}.$$
Die Amplitudenkoeffizienten $a_\nu$ können prinzipiell beliebig – aber eindeutig – den Codersymbolen $c_\nu$ zugeordnet werden. Es ist zweckmäßig, die Abstände zwischen benachbarten Amplituden gleich groß zu wählen. Bei bipolarer Signalisierung $(-1 \le a_\nu \le +1)$ gilt somit für die möglichen Amplitudenkoeffizienten mit dem Laufindex $\mu = 1$, ... , $M$:
- $$a_\mu = \frac{2\mu - M - 1}{M-1} \hspace{0.05cm}.$$
- Unabhängig von der Stufenzahl $M$ erhält man hieraus für die äußeren Amplitudenkoeffizienten $a_1 = -1$ und $a_M = +1$.
- Bei einem ternären Signal $(M = 3)$ sind die möglichen Amplitudenkoeffizienten $-1$, $0$ und $+1$.
- Bei einem Quaternärsignal $(M = 4)$ gibt es die Koeffizienten $-1$, $-1/3$, $+1/3$ und $+1$
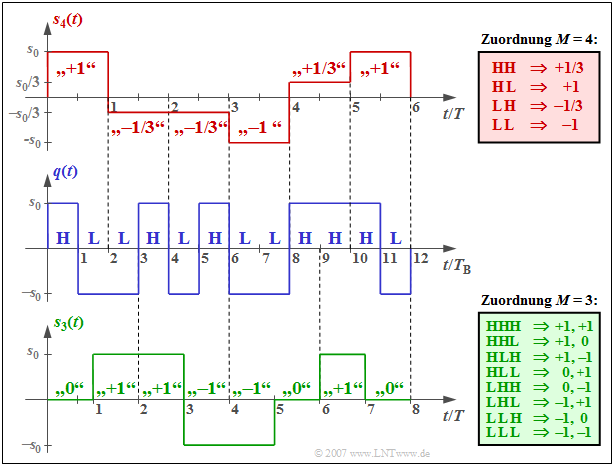
$\text{Beispiel 2:}$ Die Grafik zeigt oben das quaternäre redundanzfreie Sendesignal $s_4(t)$ mit den möglichen Amplitudenkoeffizienten $\pm 1$ und $\pm 1/3$, das sich aus dem in der Mitte dargestellten binären Quellensignal $q(t)$ ergibt.
Jeweils zwei Binärsymbole werden nach der rot hinterlegten Tabelle zu einem quaternären Amplitudenkoeffizienten zusammengefasst. Die Symboldauer $T$ des Signals $s_4(t)$ ist doppelt so groß wie die Bitdauer $T_{\rm B}$ (vorher: $T_q$) des Quellensignals.
Ist $q(t)$ redundanzfrei, so ergibt sich auch ein redundanzfreies Quaternärsignal, das heißt, die möglichen Amplitudenkoeffizienten $\pm 1$ und $\pm 1/3$ sind gleichwahrscheinlich und innerhalb der Folge $⟨a_ν⟩$ gibt es keine statistischen Bindungen.
Die untere Darstellung zeigt das (nahezu) redundanzfreie Ternärsignal $s_3(t)$ und die Zuordnung von jeweils drei Binärsymbolen zu zwei Ternärsymbolen. Die möglichen Amplitudenkoeffizienten sind $-1$, $0$ und $+1$ und es gilt $T/T_{\rm B} = 3/2$.
Man erkennt aus der angegebenen Zuordnungstabelle, dass die Amplitudenkoeffizienten $+1$ und $-1$ etwas häufiger auftreten als der Amplitudenkoeffizent$a_\nu = 0$. Hieraus ergibt sich die oben genannte relative Redundanz von $5\%$. Aus dem sehr kurzen Signalausschnitt – nur acht Ternärsymbole entsprechend zwölf Binärsymbole – ist diese Eigenschaft allerdings nicht zu erkennen.
AKF und LDS eines Mehrstufensignals
Bei einem redundanzfrei codierten $M$–stufigen bipolaren Digitalsignal $s(t)$ gilt für die diskrete Autokorrelationsfunktion (AKF) der Amplitudenkoeffizienten sowie für das entsprechende Leistungsdichtespektrum (LDS):
- $$\varphi_a(\lambda) = \left\{ \begin{array}{c} \frac{M+ 1}{3 \cdot (M-1)} \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \\ \lambda \ne 0 \\ \end{array} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\it \Phi_a(f)} = \frac{M+ 1}{3 \cdot (M-1)}= {\rm const.}$$
Unter Berücksichtigung der spektralen Formung durch den Sendegrundimpuls $g_s(t)$ mit Spektrum $G_s(f)$ erhält man:
- $$\varphi_{s}(\tau) = \frac{M+ 1}{3 \cdot (M-1)} \cdot \varphi^{^{\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}_{s}(f) = \frac{M+ 1}{3 \cdot (M-1)}\cdot |G_s(f)|^2 \hspace{0.05cm}.$$
Man erkennt aus diesen Gleichungen:
- Bei redundanzfreier mehrstufiger Codierung wird die Form von AKF und LDS allein durch den Sendegrundimpuls $g_s(t)$ bestimmt.
- Die Höhe der AKF ist bei gleicher Form gegenüber dem redundanzfreien Binärsignal um den Faktor $\varphi_a(\lambda = 0) = {\rm E}[a_\nu^2] = (M + 1)/(3M-3)$ geringer.
- Dieser Faktor beschreibt die geringere Signalleistung des Mehrstufensignals aufgrund der $M-2$ inneren Amplitudenkoeffizienten. Bei $M = 3$ ist dieser Faktor gleich $2/3$, bei $M = 4$ gleich $5/9$.
- Ein fairer Vergleich zwischen Binärsignal und Mehrstufensignal bei gleichem Informationsfluss (gleicher äquivalenter Bitrate) sollte aber auch die unterschiedlichen Symboldauern berücksichtigen.
- Dabei zeigt sich, dass ein Mehrstufensignal aufgrund des schmaleren LDS weniger Bandbreite benötigt als das Binärsignal, wenn die gleiche Information übertragen wird.
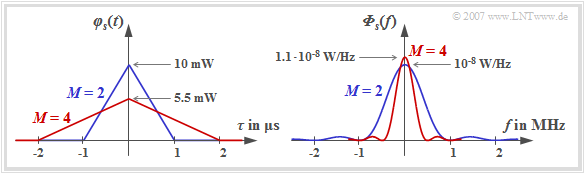
$\text{Beispiel 3:}$ Wir gehen von einer binären Quelle mit der Bitrate $R_{\rm B} = 1 \ \rm Mbit/s$ aus, so dass die Bitdauer $T_{\rm B} = 1 \ \rm \mu s$beträgt.
- Bei Binärübertragung $(M = 2)$ ist die Symboldauer $T$ des Sendesignals gleich $T_{\rm B}$ und es ergibt sich bei NRZ–Rechteckimpulsen die blau eingezeichnete AKF in der linken Grafik (vorausgesetzt ist $s_0^2 = 10 \ \rm mW$).
- Beim Quaternärsystem $(M = 4)$ ist die Autokorrelationsfunktion ebenfalls dreieckförmig, aber um den Faktor $5/9$ niedriger und wegen $T = 2 \cdot T_{\rm B}$ doppelt so breit.
Das $\rm s^2$–förmige Leistungsdichtespektrum hat im binären Fall (blaue Kurve) bei den hier gewählten Signalparametern den Maximalwert ${\it \Phi}_{s}(f = 0) = 10^{-8} \ \rm W/Hz$ (Fläche des blauen Dreiecks) und die erste Nullstelle liegt bei $f = 1 \ \rm MHz$.
- Demgegenüber ist das Leistungsdichtespektrum des Quaternärsignals (blaue Kurve) nur halb so breit und auch nur geringfügig höher. Hier gilt ${\it \Phi}_{s}(f = 0) \approx 1.1 \cdot 10^{-8} \ \rm W/Hz$
- Der Wert ergibt sich aus der Fläche des roten Dreiecks. Diese ist gegenüber dem blauen Dreieck niedriger (Faktor $0.55$) und breiter (Faktor $2$).
Fehlerwahrscheinlichkeit eines Mehrstufensystems
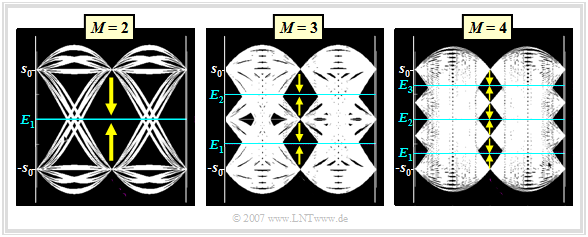
Die Grafik zeigt die Augendiagramme eines binären $(M = 2)$, eines ternären $(M = 3)$ und eines quaternären $(M = 4)$ Übertragungssystems. Hierbei ist für das Gesamtsystem $H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f)$ von Sender, Kanal und Empfänger eine Cosinus–Rolloff–Charakteristik vorausgesetzt, so dass Impulsinteferenzen keine Rolle spielen. Der Rolloff–Faktor ist $r= 0.5$. Das Rauschen wird als vernachlässigbar klein angenommen.
Das Augendiagramm wird vorwiegend zur Abschätzung von Impulsinterferenzen genutzt. Eine genaue Beschreibung folgt im Abschnitt Definition und Aussagen des Augendiagramms Der folgende Text sollte aber auch ohne Detailkenntnisse verständlich sein.
Man erkennt aus obigen Darstellungen:
Beim Binärsystem $(M = 2)$ gibt es nur eine einzige Entscheiderschwelle: $E_1 = 0$. Zu einem Übertragungsfehler kommt es, wenn die Rauschkomponente $d_{\rm N}(T_{\rm D})$ zum Detektionszeitpunkt größer ist als $+s_0$, falls $d_{\rm S}(T_{\rm D}) = -s_0$, bzw. wenn $d_{\rm N}(T_{\rm D})$ kleiner ist als $-s_0$, falls $d_{\rm S}(T_{\rm D}) = +s_0$ gilt.
Beim Ternärsystem $(M = 3)$ erkennt man zwei Augenöffnungen und zwei Entscheiderschwellen $E_1 = -s_0/2$ und $E_2 = +s_0/2$. Der Abstand der möglichen Detektionsnutzsignalwerte $d_{\rm S}(T_{\rm D})$ zu der nächstgelegenen Schwelle beträgt jeweils $-s_0/2$. Die äußeren Amplitudenwerte $(d_{\rm S}(T_{\rm D}) = \pm s_0)$ können nur in jeweils eine Richtung verfälscht werden, während $d_{\rm S}(T_{\rm D}) = 0$ von zwei Schwellen begrenzt wird.
Dementsprechend wird ein Amplitudenkoeffizient $a_\nu = 0$ gegenüber $a_\nu = +1$ bzw. $a_\nu = -1$ doppelt so oft verfälscht. Bei gleichwahrscheinlichen Amplitudenkoeffizienten sowie AWGN–Rauschen mit dem Effektivwert $\sigma_d$ ergibt sich gemäß dem Abschnitt Definition der Fehlerwahrscheinlichkeit für die Symbolfehlerwahrscheinlichkeit:
- $$p_{\rm S} = { 1}/{3} \cdot \left[{\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)+ 2 \cdot {\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)+ {\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)\right]= \frac{ 4}{3} \cdot {\rm Q} \left( \frac{s_0/2}{\sigma_d}\right)\hspace{0.05cm}.$$
Bitte beachten Sie, dass mit dieser Gleichung nicht mehr die Bitfehlerwahrscheinlichkeit $p_{\rm B}$, sondern die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ angegeben wird. Die entsprechenden Aposteriori–Kenngrößen sind Bit Error Rate (BER) bzw. Symbol Error Rate (SER). Näheres hierzu im letzten Abschnitt dieses Kapitels.
Beim Quaternärsystem $(M = 4)$ mit den möglichen Amplitudenwerten $\pm s_0$ und $\pm s_0/3$ gibt es drei Augenöffnungen und entsprechend auch drei Entscheiderschwellen bei $E_1 = -2s_0/3$, $E_2 = 0$ und $E_1 = +2s_0/3$. Unter Berücksichtigung der Auftrittswahrscheinlichkeiten (bei gleichwahrscheinlichen Symbolen jeweils $1/4$) und der sechs Verfälschungsmöglichkeiten (siehe Pfeile in der Grafik) erhält man nun:
- $$p_{\rm S} = { 6}/{4} \cdot {\rm Q} \left( \frac{s_0/3}{\sigma_d}\right)\hspace{0.05cm}.$$
$\text{Fazit:}$ Durch Erweiterung auf größere Werte von $M$ ergibt sich allgemein:
- $$p_{\rm S} = \frac{ 2 + 2 \cdot (M-2)}{M} \cdot {\rm Q} \left( \frac{s_0/(M-1)}{\sigma_d(M)}\right) = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( \frac{s_0}{\sigma_d (M)\cdot (M-1)}\right)\hspace{0.05cm}.$$
Die Schreibweise $\sigma_d(M)$ soll deutlich machen, dass der Effektivwert des Rauschanteils $d_{\rm N}(t)$ signifikant von der Stufenzahl $M$ abhängt.
Vergleich zwischen Binärsystem und Mehrstufensystem
Für diesen Systemvergleich unter fairen Bedingungen werden vorausgesetzt:
- Die äquivalente Bitrate $R_{\rm B} = 1/T_{\rm B}$ sei konstant. Abhängig von der Stufenzahl $M$ beträgt somit die Symboldauer von Codersignal und Sendesignal:
- $$T = T_{\rm B} \cdot {\rm log_2} (M) \hspace{0.05cm}.$$
- Die Nyquistbedingung wird durch eine Wurzel–Wurzel–Charakteristik mit Rolloff–Faktor $r$ erfüllt. Es treten weiterhin keine Impulsinterferenzen auf. Für die Detektionsrauschleistung gilt:
- $$\sigma_d^2 = \frac{N_0}{2T} \hspace{0.05cm}.$$
- Der Vergleich der Symbolfehlerwahrscheinlichkeiten $p_{\rm S}$ erfolgt unter der Nebenbedingung der Leistungsbegrenzung. Die Energie pro Bit beträgt bei $N$–stufiger Übertragung:
- $$E_{\rm B} = \frac{M+ 1}{3 \cdot (M-1)} \cdot s_0^2 \cdot T_{\rm B} \hspace{0.05cm}.$$
Setzt man diese Gleichungen in das allgemeine Ergebnis der letzten Seite ein, so erhält man:
- $$p_{\rm S} = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( \sqrt{\frac{s_0^2 /(M-1)^2}{\sigma_d^2}}\right) = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( \sqrt{\frac{3 \cdot {\rm log_2}\hspace{0.05cm} (M)}{M^2 -1}\cdot \frac{2 \cdot E_{\rm B}}{N_0}}\right)= K_1 \cdot {\rm Q} \left( \sqrt{K_2\cdot \frac{2 \cdot E_{\rm B}}{N_0}}\right)\hspace{0.05cm}.$$
Für $M = 2$ ist $K_1 = K_2 = 1$ zu setzen. Für größere Stufenzahlen erhält man für die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$, die sich mit $M$–stufiger redundanzfreier Codierung erreichen lässt:
- $$M = 3\text{:} \ \ K_1 = 1.333, \ K_2 = 0.594;\hspace{1cm}M = 4\text{:} \ \ K_1 = 1.500, \ K_2 = 0.400;$$
- $$M = 5\text{:} \ \ K_1 = 1.600, \ K_2 = 0.290;\hspace{1cm}M = 6\text{:} \ \ K_1 = 1.666, \ K_2 = 0.221;$$
- $$M = 7\text{:} \ \ K_1 = 1.714, \ K_2 = 0.175;\hspace{1cm}M = 8\text{:} \ \ K_1 = 1.750, \ K_2 = 0.143.$$
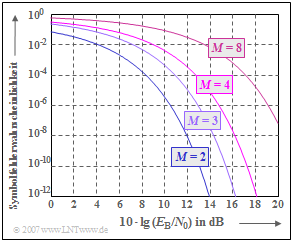
Die Grafik fasst die Ergebnisse für $M$–stufige redundanzfreie Codierung zusammen.
- Aufgetragen sind die Symbolfehlerwahrscheinlichkeiten $p_{\rm S}$ über der Abszisse $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0)$.
- Alle Systeme sind für die jeweilige Stufenzahl optimal, wenn vom AWGN–Kanal und Leistungsbegrenzung ausgegangen wird.
- Aufgrund der hier gewählten doppelt–logarithmischen Darstellung führt ein $K_2$–Wert kleiner als $1$ zu einer Parallelverschiebung der Fehlerwahrscheinlichkeitskurve nach rechts.
- Gilt $K_1 > 1$, so verschiebt sich die Kurve gegenüber dem Binärsystem $(K_1= 1)$ nach oben.
Die Kurvenverläufe kann man wie folgt interpretieren:
- Hinsichtlich Symbolfehlerwahrscheinlichkeit ist das Binärsystem $(M = 2)$ den Mehrstufensystemen überlegen. Bereits mit $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0) = 12 \ \rm dB$ ist $p_{\rm S}$ erreicht man $p_{\rm S} <10^{-8}$. Beim Quaternärsystem $(M = 4)$ muss $10 \cdot \lg \hspace{0.05cm}(E_{\rm B}/N_0) > 16 \ \rm dB$ aufgewendet werden, um gleiche Symbolfehlerwahrscheinlichkeit $p_{\rm S} =10^{-8}$ zu erreichen.
- Diese Aussage gilt jedoch nur bei verzerrungsfreiem Kanal, das heißt $H_{\rm K}(f)= 1$. Bei verzerrenden Übertragungskanälen kann dagegen ein höherstufiges System wegen der signifikant kleineren Detektionsstörleistung (nach dem Entzerrer) eine deutliche Verbesserung bringen.
- Beim AWGN–Kanal ist der einzige Vorteil einer höherstufigen Übertragung der niedrigere Bandbreitenbedarf aufgrund der kleineren äquivalenten Bitrate, der bei Basisbandübertragung nur eine untergeordnete Rolle spielt im Gegensatz zu digitalen Trägerfrequenzsystemen wie beispielsweise Quadratur–Amplitudenmodulation (QAM).
- Mit der Nebenbedingung „Spitzenwertbegrenzung” führt die Kombination aus rechteckförmigem $g_s(t)$ und rechteckförmigem $h_{\rm E}(t)$ unabhängig von der Stufenzahl $M$ zum Optimum.
- Der Verlust der Mehrstufensystemen gegenüber dem Binärsystem ist hier noch größer als bei Leistungsbegrenzung. Dies erkennt man an dem mit $M$ abnehmenden Faktor $K_2$, für den dann gilt:
- $$p_{\rm S} = K_1 \cdot {\rm Q} \left( \sqrt{K_2\cdot \frac{2 \cdot s_{\rm 0}^2 \cdot T}{N_0}}\right)\hspace{0.3cm}{\rm mit}\hspace{0.3cm} K_2 = \frac{{\rm log_2}\,(M)}{(M-1)^2} \hspace{0.05cm}.$$
Die Konstante $K_1$ ist gegenüber derobigen Angabe für Leistungsbegrenzung unverändert, während $K_2$ um den Faktor $3$ kleiner ist:
- $$M = 3\text{:} \ \ K_1 = 1.333, \ K_2 = 0.198;\hspace{1cm}M = 4\text{:} \ \ K_1 = 1.500, \ K_2 = 0.133;$$
- $$M = 5\text{:} \ \ K_1 = 1.600, \ K_2 = 0.097;\hspace{1cm}M = 6\text{:} \ \ K_1 = 1.666, \ K_2 = 0.074;$$
- $$M = 7\text{:} \ \ K_1 = 1.714, \ K_2 = 0.058;\hspace{1cm}M = 8\text{:} \ \ K_1 = 1.750, \ K_2 = 0.048.$$
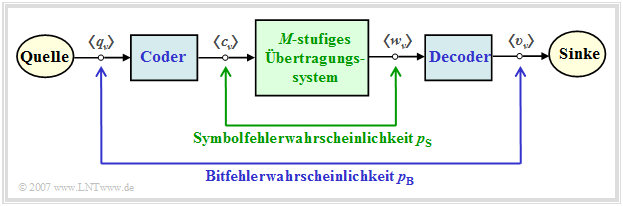
Symbol– und Bitfehlerwahrscheinlichkeit
Bei einem mehrstufigen Übertragungssystem muss man zwischen der Symbolfehlerwahrscheinlichkeit und der Bitfehlerwahrscheinlichkeit unterscheiden, die hier als Zeitmittelwerte angegeben werden:
- Die Symbolfehlerwahrscheinlichkeit bezieht sich auf die $M$–stufigen und eventuell redundanten Folgen $\langle c_\nu \rangle$ und $\langle w_\nu \rangle$:
- $$p_{\rm S} = \overline{{\rm Pr} (w_\nu \ne c_\nu)} = \lim_{N \to \infty} \frac{1}{N} \cdot \sum \limits^{N} _{\nu = 1} {\rm Pr} (w_\nu \ne c_\nu) \hspace{0.05cm}.$$
- Die Bitfehlerwahrscheinlichkeit beschreibt die Verfälschungen bezüglich der Binärfolgen $\langle q_\nu \rangle$ und $\langle v_\nu \rangle$ von Quelle und Sinke:
- $$p_{\rm B} = \overline{{\rm Pr} (v_\nu \ne q_\nu)} = \lim_{N \to \infty} \frac{1}{N} \cdot \sum \limits^{N} _{\nu = 1} {\rm Pr} (v_\nu \ne q_\nu) \hspace{0.05cm}.$$
Die Grafik veranschaulicht diese beiden Definitionen und ist auch für die nächsten Kapitel gültig. Der Block „Coder” bewirkt
- im vorliegenden Kapitel eine redundanzfreie Codierung,
- im anschließendem Kapitel eine blockweise Übertragungscodierung, und schließlich
- im letzten Kapitel die symbolweise Codierung mit Pseudoternärcodes.
$\text{Fazit:}$
- Bei mehrstufiger und(oder codierter Übertragung muss zwischen der Bitfehlerwahrscheinlichkeit $p_{\rm B}$ und der Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ unterschieden werden. Nur beim redundanzfreien Binärsystem gilt $p_{\rm B} = p_{\rm S}$.
- Im allgemeinen kann bei redundanzbehafteten Mehrstufensystem die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ etwas einfacher berechnet werden als die Bitfehlerwahrscheinlichkeit $p_{\rm B}$.
- Ein Vergleich von Systemen mit unterschiedlicher Stufenzahl oder verschiedenartiger Codierung sollte aber aus Fairnisgründen stets auf der Bitfehlerwahrscheinlichkeit $p_{\rm B}$ basieren.
- Dabei muss auch die Zuordnung zwischen den Quellen– und Codesymbolen berücksichtigt werden, wie im folgenden Beispiel gezeigt wird.
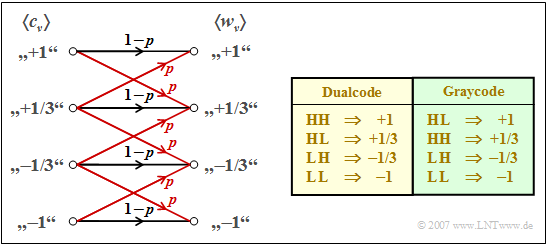
$\text{Beispiel 4:}$ Wir betrachten ein quaternäres Übertragungssystem, dessen Übertragungsverhalten wie folgt charakterisiert werden kann (siehe linke Grafik):
- Die Verfälschungswahrscheinlichkeit zu einem benachbarten Symbol ist $p={\rm Q}[s_0/(3\sigma_d)]$.
- Eine Verfälschung zu einem nicht benachbarten Symbol wird ausgeschlossen.
- Das Modell berücksichtigt die doppelten Verfälschungsmöglichkeiten der inneren Symbole.
Bei gleichwahrscheinlichen binären Quellensymbolen $q_\nu$ treten auch die quaternären Codesymbole $c_\nu$ mit gleicher Wahrscheinlichkeit auf. Damit erhält man für die Symbolfehlerwahrscheinlichkeit:
- $$p_{\rm S} ={1}/{4}\cdot (2 \cdot p + 2 \cdot 2 \cdot p) = {3}/{2} \cdot p\hspace{0.05cm}.$$
Zur Berechnung der Bitfehlerwahrscheinlichkeit muss man auch die Zuordnung zwischen den Binär– und den Quaternärsymbolen berücksichtigen:
- Bei der Dualcodierung gemäß der gelb hinterlegten Tabelle kann ein Symbolfehler $(w_\nu \ne c_\nu)$ ein oder zwei Bitfehler $(v_\nu \ne q_\nu)$ zur Folge haben. Von den sechs Verfälschungsmöglichkeiten auf Quaternärsymbolebene führen vier zu jeweils einem und nur die beiden inneren zu zwei Bitfehlern. Daraus folgt:
- $$p_{\rm B} = {1}/{4}\cdot (4 \cdot 1 \cdot p + 2 \cdot 2 \cdot p ) \cdot {1}/{2} = p\hspace{0.05cm}.$$
- Der Faktor 1/2 berücksichtigt, dass ein Quaternärsymbol zwei Binärsymbole beinhaltet.
- Dagegen ist bei der so genannten Graycodierung gemäß der grün hinterlegten Tabelle die Zuordnung zwischen den Binärsymbolen und den Quaternärsymbolen so gewählt, dass jeder Symbolfehler genau einen Bitfehler zur Folge hat. Daraus folgt:
- $$p_{\rm B} = {1}/{4}\cdot (4 \cdot 1 \cdot p + 2 \cdot 1 \cdot p ) \cdot {1}/{2} = {3}/{4} \cdot p\hspace{0.05cm}.$$
Aufgaben zum Kapitel
Aufgabe 2.3: Binärsignal und Quaternärsignal
Aufgabe 2.4: Dualcodierung und Graycodierung
Aufgabe 2.4Z: Fehlerwahrscheinlichkeiten beim Oktalsystem
Aufgabe 2.5: Ternäre Signalübertragung