Aufgaben:Exercise 1.3Z: Calculating with Complex Numbers II

• Return to book

Betrachtete Zahlen in der komplexen Ebene

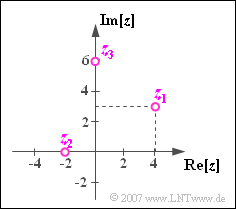
Ausgegangen wird von drei komplexen Zahlen, die rechts in der komplexen Ebene dargestellt sind:

$$z_1 = 4 + 3{\rm j},$$

$$z_2 = -2 ,$$

$$z_3 = 6{\rm j} .$$

Im Rahmen dieser Aufgabe sollen berechnet werden:

$$z_4 = z_1 \cdot z_1^{\star},$$

$$z_5 = z_1 + 2 \cdot z_2 - {z_3}/{2},$$

$$z_6 = z_1 \cdot z_2,$$

$$z_7 = {z_3}/{z_1}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Zum Rechnen mit komplexen Zahlen.
• Die Thematik wird auch im Lernvideo Rechnen mit komplexen Zahlen behandelt.
• Geben Sie Phasenwerte stets im Bereich $-\hspace{-0.05cm}180^{\circ} < \phi ≤ +180^{\circ}$ ein.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Geben Sie $z_1$ nach Betrag und Phase an.

$|z_1|\ = \ $

$\phi_1\ = \ $ $\hspace{0.1cm}\text{Grad}$

2

Wie lautet $z_4 = z_1 \cdot z_1^{\star} = x_4 + \text{j} \cdot y_4$?

$x_4\ = \ $

$y_4\ = \ $

3

Berechnen Sie $z_5 = x_5 + {\rm j} \cdot y_5$ entsprechend der Angabenseite.

$x_5\ = \ $

$y_5\ = \ $

4

Geben Sie $z_6 = z_1 \cdot z_2$ nach Betrag und Phase (im Bereich $\pm 180^{\circ}$) an.

$|z_6|\ = \ $

$\phi_6\ = \ $ $\hspace{0.1cm}\text{Grad}$

5

Welchen Phasenwert besitzt die rein imaginäre Zahl $z_3$?

$\phi_3 \ = \ $ $\hspace{0.1cm}\text{Grad}$

6

Berechnen Sie $z_7 = z_3/z_1$ nach Betrag und Phase (im Bereich $\pm 180^{\circ}$).

$|z_7| \ = \ $

$\phi_7 \ = \ $ $\hspace{0.1cm}\text{Grad}$

Musterlösung

Solution

(1)  Der Betrag kann nach dem Satz von Pythagoras berechnet werden:

$$|z_1| = \sqrt{x_1^2 + y_1^2}= \sqrt{4^2 + 3^2}\hspace{0.15cm}\underline{ = 5}.$$

Für den Phasenwinkel gilt entsprechend der Seite Darstellung nach Betrag und Phase :

$$\phi_1 = \arctan \frac{y_1}{x_1}= \arctan \frac{3}{4}\hspace{0.15cm}\underline{ = 36.9^{\circ}}.$$

(2)  Die Multiplikation von $z_1$ mit deren Konjugiert-Komplexen $z_1^{\star}$ ergibt die rein reelle Größe $z_4$, wie die folgenden Gleichungen zeigen:

$$z_4 = (x_1 + {\rm j} \cdot y_1)(x_1 - {\rm j} \cdot y_1)= {x_1^2 + y_1^2}= |z_1|^2 = 25,$$

$$z_4 = |z_1| \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}\phi_1} \cdot |z_1| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi_1}= |z_1|^2 = 25\hspace{0.3cm} \Rightarrow\hspace{0.3cm} x_4 \hspace{0.1cm}\underline{= 25}, \hspace{0.25cm}y_4 \hspace{0.15cm}\underline{= 0}.$$

(3)  Aufgeteilt nach Real- und Imaginärteil kann geschrieben werden:

$$x_5 = x_1 + 2 \cdot x_2 - {x_3}/{2} = 4 + 2 \cdot(-2) -0 \hspace{0.15cm}\underline{= 0},$$

$$y_5 = y_1 + 2 \cdot y_2 - {y_3}/{2} = 3 + 2 \cdot 0 - \frac{6}{2} \hspace{0.1cm}\underline{=0}.$$

(4)  Schreibt man $z_2$ nach Betrag und Phase   ⇒   $|z_2| = 2, \phi_2 = 180^{\circ}$, so erhält man für das Produkt:

$$|z_6| = |z_1| \cdot |z_2|= 5 \cdot 2 \hspace{0.15cm}\underline{= 10},$$

$$\phi_6 = \phi_1 + \phi_2 = 36.9^{\circ} + 180^{\circ} = 216.9^{\circ}\hspace{0.15cm}\underline{= -143.1^{\circ}}.$$

(5)  Die Phase ist $\phi_3 = 90^{\circ}$ (siehe Grafik auf der Angabenseite), wie man formal nachweisen kann:

$$\phi_3 = \arctan \left( \frac{6}{0}\right) = \arctan (\infty) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \phi_3 \hspace{0.15cm}\underline{= 90^{ \circ}}.$$

(6)  Zunächst die umständlichere Lösung:

$$z_7 = \frac{z_3}{z_1}= \frac{6{\rm j}}{4 + 3{\rm j}} = \frac{6{\rm j}\cdot(4 - 3{\rm j})}{(4 + 3{\rm j})\cdot (4 - 3{\rm j})} = \frac{18 +24{\rm j}}{25} = 1.2 \cdot{\rm e}^{{\rm j} 53.1^{ \circ}}.$$

Ein anderer Lösungsweg lautet:

$$|z_7| = \frac{|z_3|}{|z_1|} = \frac{6}{5}\hspace{0.15cm}\underline{=1.2}, \hspace{0.3cm}\phi_7 = \phi_3 - \phi_1 = 90^{\circ} - 36.9^{\circ} \hspace{0.15cm}\underline{=53.1^{\circ}}.$$