Difference between revisions of "Aufgaben:Exercise 4.2: UMTS Radio Channel Basics"
m (Guenter verschob die Seite Aufgabe 4.2: UMTS-Funkkanal nach Aufgabe 4.2: Grundlegendes zum UMTS-Funkkanal) |
|||
| Line 4: | Line 4: | ||
}} | }} | ||
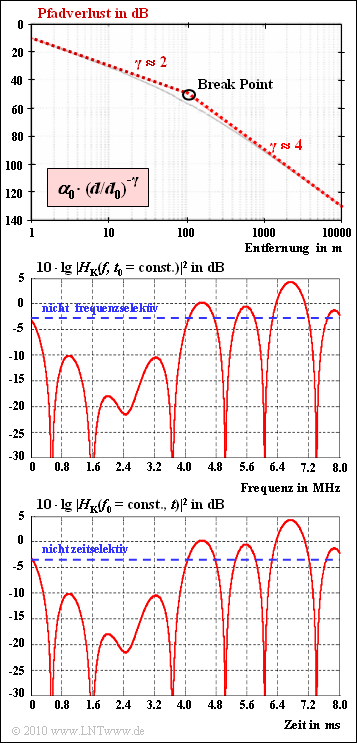
| − | [[File:P_ID1931__Bei_A_4_2.png|right|frame|Pfadverlust, | + | [[File:P_ID1931__Bei_A_4_2.png|right|frame|Pfadverlust, frequenz– und zeitselektives Fading]] |
| − | Auch bei UMTS gibt es etliche | + | Auch bei UMTS gibt es etliche zu Degradationen führende Effekte, die man bei der Systemplanung berücksichtigen muss: |
| − | *$ | + | *${\rm Interferenzen}$: Da alle Nutzer gleichzeitig im gleichen Frequenzband versorgt werden, wird jeder Nutzer durch andere Nutzer gestört. |
| − | *$ | + | *${\rm Pfadverlust}$: Die Empfangsleistung $P_{\rm E}$ eines Funksignals nimmt mit der Entfernung $d$ um den Faktor $d^{– \gamma}$ ab. |
| − | *$ | + | *${\rm Mehrwegeempfang}$: Das Signal erreicht den mobilen Empfänger nicht nur über den direkten Pfad, sondern auf mehreren Wegen – unterschiedlich gedämpft und verschieden verzögert. |
| − | *$ | + | *${\rm Dopplereffekt}$: Bewegen sich der Sender und/oder der Empfänger, so kann es zu Verschiebungen der Frequenz kommen abhängig von Geschwindigkeit und Richtung: Welcher Winkel? Aufeinander zu? Voneinander weg? |
| + | |||
| + | |||
| + | Im Buch [[Mobile Kommunikation]] wurden diese Effekte bereits im Detail behandelt. Die Diagramme vermitteln nur einige wenige Informationen bezüglich | ||
| + | *Pfadverlust: Der Pfadverlust gibt die Verminderung der Empfangsleistung mit der Entfernung $d$ vom Sender an. Oberhalb des so genannten ''Break Points'' gilt für die Empfangsleistung näherungsweise: | ||
| + | :$$\frac{P(d)}{P(d_0)} = \alpha_0 \cdot \left ( {d}/{d_0}\right )^{-4}.$$ | ||
| + | :Nach der oberen Grafik gilt $\alpha_{0} = 10^{–5}$ (entsprechend $50 \ \rm dB$) und $d_{0} = 100 \ \rm m$. | ||
| + | *Frequenzselektives Fading: Die Leistungsübertragungsfunktion $|H_{\rm K}(f)|^{2}$ zu einem gegebenen Zeitpunkt gemäß der mittleren Grafik verdeutlicht frequenzselektives Fading. Die blau–gestrichelt eingezeichnete Horizontale kennzeichnet nicht frequenzselektives Fading. | ||
| + | :Frequenzselektives Fading entsteht, wenn die Kohärenzbandbreite $B_{\rm K}$ sehr viel kleiner als die Signalbandbreite $B_{\rm S}$ ist. Dabei gilt mit der Mehrwegeverbreiterung (englisch: ''Delay Spread'') $T_{\rm V}$ ⇒ Differenz zwischen der maximalen und der minimalen Verzögerungszeit: | ||
| + | :$$B_{\rm K}\approx \frac{1}{T_{V}}= \frac{1}{\tau_{\rm max}- \tau_{\rm min}}.$$ | ||
| + | *Zeitselektives Fading: Die untere Grafik zeigt die Leistungsübertragungsfunktion $|H_{\rm K}(t)|^{2}$ für eine feste Frequenz $f_{0}$. Die Skizze ist als „schematisch” zu verstehen, weil für das hier betrachtete zeitselektive Fading genau der gleiche Verlauf gewählt wurde wie in der mittleren Grafik für das frequenzselektive Fading (reine Bequemlichkeit des Autors). | ||
| + | :Hier entsteht eine so genannte Dopplerverbreiterung $B_{\rm D}$, definiert als Differenz zwischen der maximalen und der minimalen Dopplerfrequenz. Der Kehrwert $T_{\rm D} = 1/B_{\rm D}$ wird als ''Kohärenzzeit'' oder auch als ''Korrelationsdauer'' bezeichnet. Bei UMTS tritt immer dann zeitselektives Fading auf, wenn $T_{\rm D} \ll T_{\rm C}$ (Chipdauer) ist. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ''Hinweise:'' | |
| − | |||
| − | |||
| − | Die | + | *Die Aufgabe gehört zum Themengebiet von [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_UMTS|Allgemeine Beschreibung von UMTS]]. |
| − | + | *Bezug genommen wird insbesondere auf die Seiten [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_UMTS#Eigenschaften_des_UMTS-Funkkanals|Eigenschaften des UMTS-Funkkanals]] sowie [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_UMTS#Frequenz.E2.80.93_und_zeitselektives_Fading|Frequenz– und zeitselektives Fading]]. | |
| − | + | *Die Bandbreite beträgt bei UMTS $B_{\rm S} = 5 \ \rm MHz$ und die Chipdauer ist $T_{\rm C} \approx 0.26 \ \rm µ s$. | |
| − | + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | |
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie – ausgehend von der oberen Grafik auf der Angabenseite – den Pfadverlust (in $\rm dB$) für $d = | + | {Berechnen Sie – ausgehend von der oberen Grafik auf der Angabenseite – den Pfadverlust (in $\rm dB$) für $d = \rm 5 \ km$. |
|type="{}"} | |type="{}"} | ||
${\rm Pfadverlust} \ = \ $ { 118 3% } $\ \rm dB $ | ${\rm Pfadverlust} \ = \ $ { 118 3% } $\ \rm dB $ | ||
| Line 49: | Line 48: | ||
+ Es entsteht durch Bewegung von Sender und/oder Empfänger. | + Es entsteht durch Bewegung von Sender und/oder Empfänger. | ||
+ Verschiedene Frequenzen werden unterschiedlich gedämpft. | + Verschiedene Frequenzen werden unterschiedlich gedämpft. | ||
| − | + Ein Echo im Abstand | + | + Ein Echo im Abstand $1\ \rm µ s$ führt zu frequenzselektivem Fading. |
{Welche Aussagen gelten bezüglich des zeitselektiven Fadings? | {Welche Aussagen gelten bezüglich des zeitselektiven Fadings? | ||
Revision as of 10:23, 27 February 2018
Auch bei UMTS gibt es etliche zu Degradationen führende Effekte, die man bei der Systemplanung berücksichtigen muss:
- ${\rm Interferenzen}$: Da alle Nutzer gleichzeitig im gleichen Frequenzband versorgt werden, wird jeder Nutzer durch andere Nutzer gestört.
- ${\rm Pfadverlust}$: Die Empfangsleistung $P_{\rm E}$ eines Funksignals nimmt mit der Entfernung $d$ um den Faktor $d^{– \gamma}$ ab.
- ${\rm Mehrwegeempfang}$: Das Signal erreicht den mobilen Empfänger nicht nur über den direkten Pfad, sondern auf mehreren Wegen – unterschiedlich gedämpft und verschieden verzögert.
- ${\rm Dopplereffekt}$: Bewegen sich der Sender und/oder der Empfänger, so kann es zu Verschiebungen der Frequenz kommen abhängig von Geschwindigkeit und Richtung: Welcher Winkel? Aufeinander zu? Voneinander weg?
Im Buch Mobile Kommunikation wurden diese Effekte bereits im Detail behandelt. Die Diagramme vermitteln nur einige wenige Informationen bezüglich
- Pfadverlust: Der Pfadverlust gibt die Verminderung der Empfangsleistung mit der Entfernung $d$ vom Sender an. Oberhalb des so genannten Break Points gilt für die Empfangsleistung näherungsweise:
- $$\frac{P(d)}{P(d_0)} = \alpha_0 \cdot \left ( {d}/{d_0}\right )^{-4}.$$
- Nach der oberen Grafik gilt $\alpha_{0} = 10^{–5}$ (entsprechend $50 \ \rm dB$) und $d_{0} = 100 \ \rm m$.
- Frequenzselektives Fading: Die Leistungsübertragungsfunktion $|H_{\rm K}(f)|^{2}$ zu einem gegebenen Zeitpunkt gemäß der mittleren Grafik verdeutlicht frequenzselektives Fading. Die blau–gestrichelt eingezeichnete Horizontale kennzeichnet nicht frequenzselektives Fading.
- Frequenzselektives Fading entsteht, wenn die Kohärenzbandbreite $B_{\rm K}$ sehr viel kleiner als die Signalbandbreite $B_{\rm S}$ ist. Dabei gilt mit der Mehrwegeverbreiterung (englisch: Delay Spread) $T_{\rm V}$ ⇒ Differenz zwischen der maximalen und der minimalen Verzögerungszeit:
- $$B_{\rm K}\approx \frac{1}{T_{V}}= \frac{1}{\tau_{\rm max}- \tau_{\rm min}}.$$
- Zeitselektives Fading: Die untere Grafik zeigt die Leistungsübertragungsfunktion $|H_{\rm K}(t)|^{2}$ für eine feste Frequenz $f_{0}$. Die Skizze ist als „schematisch” zu verstehen, weil für das hier betrachtete zeitselektive Fading genau der gleiche Verlauf gewählt wurde wie in der mittleren Grafik für das frequenzselektive Fading (reine Bequemlichkeit des Autors).
- Hier entsteht eine so genannte Dopplerverbreiterung $B_{\rm D}$, definiert als Differenz zwischen der maximalen und der minimalen Dopplerfrequenz. Der Kehrwert $T_{\rm D} = 1/B_{\rm D}$ wird als Kohärenzzeit oder auch als Korrelationsdauer bezeichnet. Bei UMTS tritt immer dann zeitselektives Fading auf, wenn $T_{\rm D} \ll T_{\rm C}$ (Chipdauer) ist.
Hinweise:
- Die Aufgabe gehört zum Themengebiet von Allgemeine Beschreibung von UMTS.
- Bezug genommen wird insbesondere auf die Seiten Eigenschaften des UMTS-Funkkanals sowie Frequenz– und zeitselektives Fading.
- Die Bandbreite beträgt bei UMTS $B_{\rm S} = 5 \ \rm MHz$ und die Chipdauer ist $T_{\rm C} \approx 0.26 \ \rm µ s$.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(1) Entsprechend der Skizze liegt der Breakpoint bei $d_{0} = 100 \ \rm m$. Für $d ≤ d_{0}$ ist der Pfadverlust gleich $\alpha_{0} \cdot (d/d_{0})^{–2}$. Für $d = d_{0} = 100 \ \rm m$ gilt:
- $${\rm Pfadverlust} = \alpha_0 = 10^{-5}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}{50\,{\rm dB}}.$$
Oberhalb von $d_{0}$ ist der Pfadverlust gleich $\alpha_{0} \cdot ((d/d_{0})^{–4}$. Somit erhält man in $5 \ \rm km$ Entfernung:
- $${\rm Pfadverlust} = 10^{-5}\cdot 50^{-4} = 1.6 \cdot 10^{-12}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}\underline{118\,{\rm dB}}.$$
(2) Richtig sind die Aussagen 1, 3 und 4. Das frequenzselektive Fading ist auf Mehrwegeempfang zurückzuführen: Unterschiedliche Frequenzanteile werden durch den Kanal unterschiedlich verzögert und gedämpft und es entstehen dadurch Dämpfungs– und Phasenverzerrungen. Wegen $\tau_{\rm max} = 1 \ \rm \mu s$ (vereinfachend wird $\tau_{\rm min} = 0$ gesetzt) ergibt sich weiter
- $$B_{\rm K} = \frac{1}{\tau_{\rm max}- \tau_{\rm min}} = 1\,{\rm MHz} << B_{\rm S} \hspace{0.15cm}\underline {= 5\,{\rm MHz}}.$$
(3) Richtig ist Aussage 2. Die Aussagen 1 und 3 würden für frequenzselektives Fading gelten.