Difference between revisions of "Theory of Stochastic Signals/Poisson Distribution"
| Line 8: | Line 8: | ||
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Die '''Poissonverteilung''' ist ein Grenzfall der [[Stochastische_Signaltheorie/Binomialverteilung#Allgemeine_Beschreibung_der_Binomialverteilung|Binomialverteilung]], wobei | + | $\text{Definition:}$ Die '''Poissonverteilung''' ist ein Grenzfall der [[Stochastische_Signaltheorie/Binomialverteilung#Allgemeine_Beschreibung_der_Binomialverteilung|Binomialverteilung]], wobei |
| − | *zum einen von den Grenzübergängen $I → ∞$ und $p → 0$ ausgegangen wird, | + | *zum einen von den Grenzübergängen $I → ∞$ und $p → 0$ ausgegangen wird, |
| − | *zusätzlich vorausgesetzt ist, dass das Produkt $I · p = λ$ einen endlichen Wert besitzt. | + | *zusätzlich vorausgesetzt ist, dass das Produkt $I · p = λ$ einen endlichen Wert besitzt. |
| − | Der Parameter $λ$ gibt die mittlere Anzahl der „Einsen” in einer festgelegten Zeiteinheit an und wird als die '''Rate''' bezeichnet. }} | + | Der Parameter $λ$ gibt die mittlere Anzahl der „Einsen” in einer festgelegten Zeiteinheit an und wird als die '''Rate''' bezeichnet. }} |
Weiter ist anzumerken: | Weiter ist anzumerken: | ||
| − | *Im Gegensatz zur Binomialverteilung $(0 ≤ μ ≤ I)$ kann hier die Zufallsgröße beliebig große (ganzzahlige, nichtnegative) Werte annehmen. | + | *Im Gegensatz zur Binomialverteilung $(0 ≤ μ ≤ I)$ kann hier die Zufallsgröße beliebig große (ganzzahlige, nichtnegative) Werte annehmen. |
* Das bedeutet, dass die Menge der möglichen Werte hier nicht abzählbar ist. | * Das bedeutet, dass die Menge der möglichen Werte hier nicht abzählbar ist. | ||
| − | *Da jedoch keine Zwischenwerte auftreten können, spricht man auch hier von einer ''diskreten Verteilung''. | + | *Da jedoch keine Zwischenwerte auftreten können, spricht man auch hier von einer ''diskreten Verteilung''. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Berechnungsvorschrift:}$ Berücksichtigt man | + | $\text{Berechnungsvorschrift:}$ |
| + | |||
| + | Berücksichtigt man obige Grenzübergänge bei den [[Stochastische_Signaltheorie/Binomialverteilung#Wahrscheinlichkeiten_der_Binomialverteilung|Wahrscheinlichkeiten der Binomialverteilung]], so folgt für die '''Wahrscheinlichkeiten der Poissonverteilung''' : | ||
:$$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$ | :$$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$ | ||
Daraus erhält man nach einigen algebraischen Umformungen: | Daraus erhält man nach einigen algebraischen Umformungen: | ||
| Line 31: | Line 33: | ||
[[File: P_ID615__Sto_T_2_4_S1_neu.png |frame| Wahrscheinlichkeiten der Poissonverteilung | rechts]] | [[File: P_ID615__Sto_T_2_4_S1_neu.png |frame| Wahrscheinlichkeiten der Poissonverteilung | rechts]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 1:}$ Die Wahrscheinlichkeiten | + | $\text{Beispiel 1:}$ Die Wahrscheinlichkeiten |
| − | *Binomialverteilung mit $I =6$, $p = 0.4$, und | + | *der Binomialverteilung mit $I =6$, $p = 0.4$, und |
| − | *Poissonverteilung mit $λ = 2.4$ | + | *der Poissonverteilung mit $λ = 2.4$ |
sind der nebenstehenden Grafik zu entnehmen. Man erkennt: | sind der nebenstehenden Grafik zu entnehmen. Man erkennt: | ||
| − | *Beide Verteilungen besitzen den gleichen Mittelwert $m_1 = 2.4$. | + | *Beide Verteilungen besitzen den gleichen Mittelwert $m_1 = 2.4$. |
| − | *Bei der Poissonverteilung (rote Pfeile und Beschriftung) sind die „äußeren Werte” wahrscheinlicher als bei der Binomialverteilung. | + | *Bei der Poissonverteilung (rote Pfeile und Beschriftung) sind die „äußeren Werte” wahrscheinlicher als bei der Binomialverteilung. |
| − | *Zudem sind bei der Poissonverteilung auch Zufallsgrößen $z > 6$ möglich | + | *Zudem sind bei der Poissonverteilung auch Zufallsgrößen $z > 6$ möglich; deren Wahrscheinlichkeiten sind bei der gewählten Rate aber auch eher klein. }} |
==Momente der Poissonverteilung== | ==Momente der Poissonverteilung== | ||
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Berechnungsvorschrift:}$ Mittelwert und Streuung der Poissonverteilung ergeben sich direkt aus den entsprechenden [[Stochastische_Signaltheorie/Binomialverteilung#Momente_der_Binomialverteilung|Gleichungen der Binomialverteilung]] durch zweifache Grenzwertbildung: | + | $\text{Berechnungsvorschrift:}$ |
| + | |||
| + | Mittelwert und Streuung der Poissonverteilung ergeben sich direkt aus den entsprechenden [[Stochastische_Signaltheorie/Binomialverteilung#Momente_der_Binomialverteilung|Gleichungen der Binomialverteilung]] durch zweifache Grenzwertbildung: | ||
:$$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} I \cdot p= \lambda,$$ | :$$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} I \cdot p= \lambda,$$ | ||
:$$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$ | :$$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$ | ||
| − | Daraus ist ersichtlich, dass bei der Poissonverteilung stets $σ^2 = m_1 = λ$ gilt. }} | + | Daraus ist ersichtlich, dass bei der Poissonverteilung stets $σ^2 = m_1 = λ$ gilt. }} |
| Line 55: | Line 59: | ||
$\text{Beispiel 2:}$ | $\text{Beispiel 2:}$ | ||
| − | Wie im $\text{Beispiel 1}$ werden hier miteinander verglichen: | + | Wie im $\text{Beispiel 1}$ werden hier miteinander verglichen: |
| − | *die Binomialverteilung mit $I =6$, $p = 0.4$, und | + | *die Binomialverteilung mit $I =6$, $p = 0.4$, und |
| − | *und die Poissonverteilung mit $λ = 2.4$ | + | *und die Poissonverteilung mit $λ = 2.4$ |
| + | |||
Man erkennt aus der nebenstehenden Skizze: | Man erkennt aus der nebenstehenden Skizze: | ||
| − | *Beide Verteilungen besitzen genau den gleichen Mittelwert $m_1 = 2.4$. | + | *Beide Verteilungen besitzen genau den gleichen Mittelwert $m_1 = 2.4$. |
| − | *Bei der Poissonverteilung (im Bild rot markiert) beträgt die Streuung $σ ≈ 1.55$. | + | *Bei der Poissonverteilung (im Bild rot markiert) beträgt die Streuung $σ ≈ 1.55$. |
| − | *Bei der (blauen) Binomialverteilung ist die Standardabweichung dagegen nur $σ = 1.2$.}} | + | *Bei der (blauen) Binomialverteilung ist die Standardabweichung dagegen nur $σ = 1.2$.}} |
| − | Mit dem interaktiven Applet [[Applets:Binomial-_und_Poissonverteilung_(Applet)|Binomial– und Poissonverteilung]] können Sie die Wahrscheinlichkeiten und Mittelwerte der Poissonverteilung für beliebige $λ$–Werte ermitteln und sich die Gemeinsamkeiten und Unterschiede gegenüber der Binomialverteilung verdeutlichen. | + | Mit dem interaktiven Applet [[Applets:Binomial-_und_Poissonverteilung_(Applet)|Binomial– und Poissonverteilung]] können Sie die Wahrscheinlichkeiten und Mittelwerte (Momente) der Poissonverteilung für beliebige $λ$–Werte ermitteln und sich die Gemeinsamkeiten und Unterschiede gegenüber der Binomialverteilung verdeutlichen. |
| Line 73: | Line 78: | ||
Nun sollen sowohl die Gemeinsamkeiten als auch die Unterschiede zwischen binomial– und poissonverteilten Zufallsgrößen nochmals herausgearbeitet werden. | Nun sollen sowohl die Gemeinsamkeiten als auch die Unterschiede zwischen binomial– und poissonverteilten Zufallsgrößen nochmals herausgearbeitet werden. | ||
| − | Die '''Binomialverteilung''' ist zur Beschreibung von solchen stochastischen Ereignissen geeignet, die durch einen vorgegebenen Takt $T$ gekennzeichnet sind. Beispielsweise beträgt bei [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_ISDN|ISDN]] (''Integrated Services Digital Network'') mit $64 \ \rm kbit/s$ die Taktzeit $T \approx 15.6 \ \rm µ s$. | + | Die '''Binomialverteilung''' ist zur Beschreibung von solchen stochastischen Ereignissen geeignet, die durch einen vorgegebenen Takt $T$ gekennzeichnet sind. Beispielsweise beträgt bei [[Beispiele_von_Nachrichtensystemen/Allgemeine_Beschreibung_von_ISDN|ISDN]] (''Integrated Services Digital Network'') mit $64 \ \rm kbit/s$ die Taktzeit $T \approx 15.6 \ \rm µ s$. |
| − | *Nur in diesem Zeitraster treten binäre Ereignisse auf. Solche Ereignisse sind zum Beispiel die fehlerfreie $(e_i = 0)$ oder fehlerhafte $(e_i = 1)$ Übertragung einzelner Symbole. | + | *Nur in diesem Zeitraster treten binäre Ereignisse auf. Solche Ereignisse sind zum Beispiel die fehlerfreie $(e_i = 0)$ oder fehlerhafte $(e_i = 1)$ Übertragung einzelner Symbole. |
| − | *Die Binomialverteilung ermöglicht nun statistische Aussagen über die Anzahl der in einem längeren Zeitintervall $T_{\rm I} = I · T$ zu erwartenden Übertragungsfehler entsprechend | + | *Die Binomialverteilung ermöglicht nun statistische Aussagen über die Anzahl der in einem längeren Zeitintervall $T_{\rm I} = I · T$ zu erwartenden Übertragungsfehler entsprechend dem oberen Diagramm der folgenden Grafik (blau markierte Zeitpunkte). |
[[File: P_ID60__Sto_T_2_4_S3_neu.png |center|frame| Schema für Binomialverteilung und Poissonverteilung]] | [[File: P_ID60__Sto_T_2_4_S3_neu.png |center|frame| Schema für Binomialverteilung und Poissonverteilung]] | ||
| − | Auch die '''Poissonverteilung''' macht Aussagen über die Anzahl eintretender Binärereignisse in einem endlichen Zeitintervall: | + | Auch die '''Poissonverteilung''' macht Aussagen über die Anzahl eintretender Binärereignisse in einem endlichen Zeitintervall: |
| − | *Geht man hierbei vom gleichen Betrachtungszeitraum $T_{\rm I}$ aus und vergrößert die Anzahl $I$ der Teilintervalle immer mehr, so wird die Taktzeit $T$, zu der jeweils ein neues Binärereignis („0” oder „1”) eintreten kann, immer kleiner. Im Grenzfall geht $T$ gegen Null. | + | *Geht man hierbei vom gleichen Betrachtungszeitraum $T_{\rm I}$ aus und vergrößert die Anzahl $I$ der Teilintervalle immer mehr, so wird die Taktzeit $T$, zu der jeweils ein neues Binärereignis („0” oder „1”) eintreten kann, immer kleiner. Im Grenzfall geht $T$ gegen Null. |
| − | *Das heißt: Bei der Poissonverteilung sind die binären Ereignisse nicht nur zu diskreten, durch ein Zeitraster vorgegebenen Zeitpunkten möglich, sondern jederzeit. Das untere Zeitdiagramm verdeutlicht diesen Sachverhalt. | + | *Das heißt: Bei der Poissonverteilung sind die binären Ereignisse nicht nur zu diskreten, durch ein Zeitraster vorgegebenen Zeitpunkten möglich, sondern jederzeit. Das untere Zeitdiagramm verdeutlicht diesen Sachverhalt. |
| − | *Um im Mittel während der Zeit $T_{\rm I}$ genau so viele „Einsen” wie bei der Binomialverteilung zu erhalten (im Beispiel: sechs), muss allerdings die auf das infinitesimal kleine Zeitintervall $T$ bezogene charakteristische Wahrscheinlichkeit $p = {\rm Pr}( e_i = 1)$ gegen Null tendieren. | + | *Um im Mittel während der Zeit $T_{\rm I}$ genau so viele „Einsen” wie bei der Binomialverteilung zu erhalten (im Beispiel: sechs), muss allerdings die auf das infinitesimal kleine Zeitintervall $T$ bezogene charakteristische Wahrscheinlichkeit $p = {\rm Pr}( e_i = 1)$ gegen Null tendieren. |
==Anwendungen der Poissonverteilung== | ==Anwendungen der Poissonverteilung== | ||
<br> | <br> | ||
| − | Die Poissonverteilung ist das Ergebnis eines so genannten [https://de.wikipedia.org/wiki/Poisson-Prozess Poissonprozesses]. Ein solcher dient häufig als Modell für | + | Die Poissonverteilung ist das Ergebnis eines so genannten [https://de.wikipedia.org/wiki/Poisson-Prozess Poissonprozesses]. Ein solcher dient häufig als Modell für Ereignisfolgen, die zu zufälligen Zeitpunkten eintreten können. Beispiele für derartige Ereignisse sind |
*der Ausfall von Geräten – eine wichtige Aufgabenstellung in der Zuverlässigkeitstheorie, | *der Ausfall von Geräten – eine wichtige Aufgabenstellung in der Zuverlässigkeitstheorie, | ||
*das Schrotrauschen bei der optischen Übertragung, und | *das Schrotrauschen bei der optischen Übertragung, und | ||
| − | *der Beginn von Telefongesprächen in einer Vermittlungsstelle („Verkehrstheorie”). | + | *der Beginn von Telefongesprächen in einer Vermittlungsstelle („Verkehrstheorie”). |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 3:}$ Gehen bei einer Vermittlungsstelle im Langzeitmittel neunzig Vermittlungswünsche pro Minute (also $λ = 1.5 \text{ pro Sekunde}$ | + | $\text{Beispiel 3:}$ Gehen bei einer Vermittlungsstelle im Langzeitmittel neunzig Vermittlungswünsche pro Minute $($also $λ = 1.5 \text{ pro Sekunde})$ ein, so lauten die Wahrscheinlichkeiten $p_\mu$, dass in einem beliebigen Zeitraum von einer Sekunde genau $\mu$ Belegungen auftreten: |
:$$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$ | :$$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$ | ||
| Line 101: | Line 106: | ||
Daraus lassen sich weitere Kenngrößen ableiten: | Daraus lassen sich weitere Kenngrößen ableiten: | ||
| − | *Die Abstand $τ$ zwischen zwei Vermittlungswünschen genügt der [[Stochastische_Signaltheorie/Exponentialverteilte_Zufallsgrößen#Einseitige_Exponentialverteilung|Exponentialverteilung]]. | + | *Die Abstand $τ$ zwischen zwei Vermittlungswünschen genügt der [[Stochastische_Signaltheorie/Exponentialverteilte_Zufallsgrößen#Einseitige_Exponentialverteilung|Exponentialverteilung]]. |
| − | *Die mittlere Zeitspanne zwischen zwei Vermittlungswünschen beträgt ${\rm E}[τ] = 1/λ ≈ 0.667 \ \rm s$.}} | + | *Die mittlere Zeitspanne zwischen zwei Vermittlungswünschen beträgt ${\rm E}[\hspace{0.05cm}τ\hspace{0.05cm}] = 1/λ ≈ 0.667 \ \rm s$.}} |
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
Revision as of 15:12, 13 November 2019
Contents
Wahrscheinlichkeiten der Poissonverteilung
$\text{Definition:}$ Die Poissonverteilung ist ein Grenzfall der Binomialverteilung, wobei
- zum einen von den Grenzübergängen $I → ∞$ und $p → 0$ ausgegangen wird,
- zusätzlich vorausgesetzt ist, dass das Produkt $I · p = λ$ einen endlichen Wert besitzt.
Der Parameter $λ$ gibt die mittlere Anzahl der „Einsen” in einer festgelegten Zeiteinheit an und wird als die Rate bezeichnet.
Weiter ist anzumerken:
- Im Gegensatz zur Binomialverteilung $(0 ≤ μ ≤ I)$ kann hier die Zufallsgröße beliebig große (ganzzahlige, nichtnegative) Werte annehmen.
- Das bedeutet, dass die Menge der möglichen Werte hier nicht abzählbar ist.
- Da jedoch keine Zwischenwerte auftreten können, spricht man auch hier von einer diskreten Verteilung.
$\text{Berechnungsvorschrift:}$
Berücksichtigt man obige Grenzübergänge bei den Wahrscheinlichkeiten der Binomialverteilung, so folgt für die Wahrscheinlichkeiten der Poissonverteilung :
- $$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$
Daraus erhält man nach einigen algebraischen Umformungen:
- $$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$
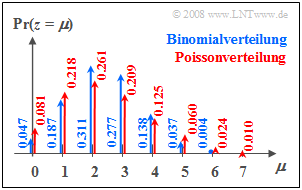
$\text{Beispiel 1:}$ Die Wahrscheinlichkeiten
- der Binomialverteilung mit $I =6$, $p = 0.4$, und
- der Poissonverteilung mit $λ = 2.4$
sind der nebenstehenden Grafik zu entnehmen. Man erkennt:
- Beide Verteilungen besitzen den gleichen Mittelwert $m_1 = 2.4$.
- Bei der Poissonverteilung (rote Pfeile und Beschriftung) sind die „äußeren Werte” wahrscheinlicher als bei der Binomialverteilung.
- Zudem sind bei der Poissonverteilung auch Zufallsgrößen $z > 6$ möglich; deren Wahrscheinlichkeiten sind bei der gewählten Rate aber auch eher klein.
Momente der Poissonverteilung
$\text{Berechnungsvorschrift:}$
Mittelwert und Streuung der Poissonverteilung ergeben sich direkt aus den entsprechenden Gleichungen der Binomialverteilung durch zweifache Grenzwertbildung:
- $$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} I \cdot p= \lambda,$$
- $$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$
Daraus ist ersichtlich, dass bei der Poissonverteilung stets $σ^2 = m_1 = λ$ gilt.
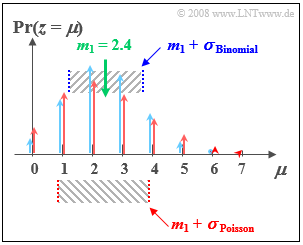
$\text{Beispiel 2:}$
Wie im $\text{Beispiel 1}$ werden hier miteinander verglichen:
- die Binomialverteilung mit $I =6$, $p = 0.4$, und
- und die Poissonverteilung mit $λ = 2.4$
Man erkennt aus der nebenstehenden Skizze:
- Beide Verteilungen besitzen genau den gleichen Mittelwert $m_1 = 2.4$.
- Bei der Poissonverteilung (im Bild rot markiert) beträgt die Streuung $σ ≈ 1.55$.
- Bei der (blauen) Binomialverteilung ist die Standardabweichung dagegen nur $σ = 1.2$.
Mit dem interaktiven Applet Binomial– und Poissonverteilung können Sie die Wahrscheinlichkeiten und Mittelwerte (Momente) der Poissonverteilung für beliebige $λ$–Werte ermitteln und sich die Gemeinsamkeiten und Unterschiede gegenüber der Binomialverteilung verdeutlichen.
Gegenüberstellung Binomialverteilung vs. Poissonverteilung
Nun sollen sowohl die Gemeinsamkeiten als auch die Unterschiede zwischen binomial– und poissonverteilten Zufallsgrößen nochmals herausgearbeitet werden.
Die Binomialverteilung ist zur Beschreibung von solchen stochastischen Ereignissen geeignet, die durch einen vorgegebenen Takt $T$ gekennzeichnet sind. Beispielsweise beträgt bei ISDN (Integrated Services Digital Network) mit $64 \ \rm kbit/s$ die Taktzeit $T \approx 15.6 \ \rm µ s$.
- Nur in diesem Zeitraster treten binäre Ereignisse auf. Solche Ereignisse sind zum Beispiel die fehlerfreie $(e_i = 0)$ oder fehlerhafte $(e_i = 1)$ Übertragung einzelner Symbole.
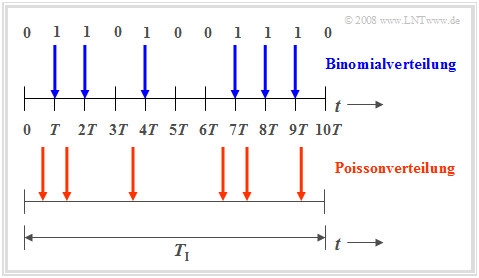
- Die Binomialverteilung ermöglicht nun statistische Aussagen über die Anzahl der in einem längeren Zeitintervall $T_{\rm I} = I · T$ zu erwartenden Übertragungsfehler entsprechend dem oberen Diagramm der folgenden Grafik (blau markierte Zeitpunkte).
Auch die Poissonverteilung macht Aussagen über die Anzahl eintretender Binärereignisse in einem endlichen Zeitintervall:
- Geht man hierbei vom gleichen Betrachtungszeitraum $T_{\rm I}$ aus und vergrößert die Anzahl $I$ der Teilintervalle immer mehr, so wird die Taktzeit $T$, zu der jeweils ein neues Binärereignis („0” oder „1”) eintreten kann, immer kleiner. Im Grenzfall geht $T$ gegen Null.
- Das heißt: Bei der Poissonverteilung sind die binären Ereignisse nicht nur zu diskreten, durch ein Zeitraster vorgegebenen Zeitpunkten möglich, sondern jederzeit. Das untere Zeitdiagramm verdeutlicht diesen Sachverhalt.
- Um im Mittel während der Zeit $T_{\rm I}$ genau so viele „Einsen” wie bei der Binomialverteilung zu erhalten (im Beispiel: sechs), muss allerdings die auf das infinitesimal kleine Zeitintervall $T$ bezogene charakteristische Wahrscheinlichkeit $p = {\rm Pr}( e_i = 1)$ gegen Null tendieren.
Anwendungen der Poissonverteilung
Die Poissonverteilung ist das Ergebnis eines so genannten Poissonprozesses. Ein solcher dient häufig als Modell für Ereignisfolgen, die zu zufälligen Zeitpunkten eintreten können. Beispiele für derartige Ereignisse sind
- der Ausfall von Geräten – eine wichtige Aufgabenstellung in der Zuverlässigkeitstheorie,
- das Schrotrauschen bei der optischen Übertragung, und
- der Beginn von Telefongesprächen in einer Vermittlungsstelle („Verkehrstheorie”).
$\text{Beispiel 3:}$ Gehen bei einer Vermittlungsstelle im Langzeitmittel neunzig Vermittlungswünsche pro Minute $($also $λ = 1.5 \text{ pro Sekunde})$ ein, so lauten die Wahrscheinlichkeiten $p_\mu$, dass in einem beliebigen Zeitraum von einer Sekunde genau $\mu$ Belegungen auftreten:
- $$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$
Es ergeben sich die Zahlenwerte $p_0 = 0.223$, $p_1 = 0.335$, $p_2 = 0.251$, usw.
Daraus lassen sich weitere Kenngrößen ableiten:
- Die Abstand $τ$ zwischen zwei Vermittlungswünschen genügt der Exponentialverteilung.
- Die mittlere Zeitspanne zwischen zwei Vermittlungswünschen beträgt ${\rm E}[\hspace{0.05cm}τ\hspace{0.05cm}] = 1/λ ≈ 0.667 \ \rm s$.
Aufgaben zum Kapitel
Aufgabe 2.5: „Binomial” oder „Poisson”?