Difference between revisions of "Aufgaben:Exercise 3.5: GMSK Modulation"
From LNTwww
m (Javier moved page Exercises:Exercise 3.5: GMSK Modulation to Exercise 3.5: GMSK Modulation: Text replacement - "Exercises:Exercise" to "Aufgaben:Exercise") |
|||
| Line 11: | Line 11: | ||
The graphic illustrates the situation: | The graphic illustrates the situation: | ||
| − | *The digital message is represented by the amplitude coefficients $a_{\mu} ∈ \{±1\}$ which are applied to a Dirac pulse. It should be noted that the sequence drawn in is assumed for the subtask '''(3)''. | + | *The digital message is represented by the amplitude coefficients $a_{\mu} ∈ \{±1\}$ which are applied to a Dirac pulse. It should be noted that the sequence drawn in is assumed for the subtask '''(3)'''. |
*The symmetrical rectangular pulse with duration $T = T_{\rm B}$ (GSM bit duration) is dimensionless: | *The symmetrical rectangular pulse with duration $T = T_{\rm B}$ (GSM bit duration) is dimensionless: | ||
| Line 19: | Line 19: | ||
*The Gaussian low pass is given by its frequency response or impulse response: | *The Gaussian low pass is given by its frequency response or impulse response: | ||
:$$H_{\rm G}(f) = {\rm e}^{-\pi\cdot (\frac{f}{2 f_{\rm G}})^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\cdot (2 f_{\rm G}\cdot t)^2}\hspace{0.05cm},$$ | :$$H_{\rm G}(f) = {\rm e}^{-\pi\cdot (\frac{f}{2 f_{\rm G}})^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\cdot (2 f_{\rm G}\cdot t)^2}\hspace{0.05cm},$$ | ||
| − | : | + | :where the system theoretical cut-off frequency $f_{\rm G}$ is used. In the GSM specification, however, the 3dB cut-off frequency is specified with $f_{\rm 3dB} = 0.3/T$ . From this, $f_{\rm G}$ can be calculated directly - see subtask '''(2)'''. |
| − | * | + | *The signal after the gauss low pass is thus |
:$$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$ | :$$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$ | ||
| − | + | Here $g(t)$ is referred to as ''frequency pulse''. For this one: | |
:$$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$ | :$$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$ | ||
| − | * | + | *With the low pass filtered signal $q_{\rm G}(t)$, the carrier frequency $f_{\rm T}$ and the frequency deviation $\Delta f_{\rm A}$ can thus be written for the instantaneous frequency at the output of the FSK modulator::$$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$ |
| − | :$$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$ | ||
| Line 38: | Line 37: | ||
*This exercise belongs to the chapter [[Mobile_Kommunikation/Die_Charakteristika_von_GSM|Die Charakteristika von GSM]]. | *This exercise belongs to the chapter [[Mobile_Kommunikation/Die_Charakteristika_von_GSM|Die Charakteristika von GSM]]. | ||
| − | * | + | *Reference is also made to the chapter [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle|Funkschnittstelle]] in the book „Beispiele von Nachrichtensystemen”. |
| − | * | + | *For your calculations use the exemplary values $f_{\rm T} = 900 \ \ \rm MHz$ and $\Delta f_{\rm A} = 68 \ \rm kHz$. |
| − | * | + | *Use the Gaussian integral to solve the task (some numerical values are given in the table) |
| − | [[File:P_ID2226__Bei_A_3_4b.png|right|frame| | + | [[File:P_ID2226__Bei_A_3_4b.png|right|frame|some values of the Gaussian integral]] |
:$$\phi(x) =\frac {1}{\sqrt{2 \pi}} \cdot \int^{x} _{-\infty} {\rm e}^{-u^2/2}\,{\rm d}u \hspace{0.05cm}.$$ | :$$\phi(x) =\frac {1}{\sqrt{2 \pi}} \cdot \int^{x} _{-\infty} {\rm e}^{-u^2/2}\,{\rm d}u \hspace{0.05cm}.$$ | ||
<br clear=all> | <br clear=all> | ||
| Line 52: | Line 51: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {In | + | {In what range of values can the instantaneous frequency $f_{\rm A}(t)$ fluctuate? Which requirements must be met? |
|type="{}"} | |type="{}"} | ||
${\rm Max} \ \big[f_{\rm A}(t)\big] \ = \hspace{0.2cm} $ { 900.068 0.01% } $\ \rm MHz$ | ${\rm Max} \ \big[f_{\rm A}(t)\big] \ = \hspace{0.2cm} $ { 900.068 0.01% } $\ \rm MHz$ | ||
${\rm Min} \ \big[f_{\rm A}(t)\big] \ = \hspace{0.28cm} $ { 899.932 0.01% } $\ \rm MHz$ | ${\rm Min} \ \big[f_{\rm A}(t)\big] \ = \hspace{0.28cm} $ { 899.932 0.01% } $\ \rm MHz$ | ||
| − | { | + | {Which (normalized) system-theoretical cut-off frequency of the Gaussian low pass results from the requirement $f_{\rm 3dB} \cdot T = 0.3$? |
|type="{}"} | |type="{}"} | ||
$f_{\rm G} \cdot T \ = \ $ { 0.45 3% } | $f_{\rm G} \cdot T \ = \ $ { 0.45 3% } | ||
| − | { | + | {Calculate the frequency pulse $g(t)$ using the function $\phi (x)$. How large is the pulse value $g(t = 0)$? |
|type="{}"} | |type="{}"} | ||
$g(t = 0) \ = \ $ { 0.737 3% } | $g(t = 0) \ = \ $ { 0.737 3% } | ||
| − | { | + | {Which signal value results for $q_{\rm G}(t = 3T)$ with $a_{3} = -1$ and $a_{\mu \ne 3} = +1$? What is the instantaneous frequency $f_{\rm A}(t = 3T)$? |
|type="{}"} | |type="{}"} | ||
$q_{\rm G}(t = 3T) \ = \ $ { -0.51822--0.42978 } | $q_{\rm G}(t = 3T) \ = \ $ { -0.51822--0.42978 } | ||
| − | { | + | {Calculate the pulse values $g(t = ±T)$ of the frequency pulse |
|type="{}"} | |type="{}"} | ||
$g(t = ±T) \ = \ $ { 0.131 3% } | $g(t = ±T) \ = \ $ { 0.131 3% } | ||
| − | { | + | {The amplitude coefficients are alternating. What is the maximum amount of $q_{G}(t)$ ? Consider $g(t ≥ 2 T) \approx 0$. |
|type="{}"} | |type="{}"} | ||
${\rm Max} \ |q_{\rm G}(t)| \ = \ $ { 0.475 3% } | ${\rm Max} \ |q_{\rm G}(t)| \ = \ $ { 0.475 3% } | ||
| Line 84: | Line 83: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' If all amplitude coefficients $a_{\mu}$ are equal to $+1$, then $q_{\rm R}(t) = 1$ is a constant. Thus, the Gaussian low pass has no influence and $q_{\rm G}(t) = 1$ results. |
| − | * | + | *The maximum frequency is thus |
:$${\rm Max}\ [f_{\rm A}(t)] = f_{\rm T} + \Delta f_{\rm A} \hspace{0.15cm} \underline {= 900.068\,{\rm MHz}} \hspace{0.05cm}.$$ | :$${\rm Max}\ [f_{\rm A}(t)] = f_{\rm T} + \Delta f_{\rm A} \hspace{0.15cm} \underline {= 900.068\,{\rm MHz}} \hspace{0.05cm}.$$ | ||
| − | * | + | *The minimum instantaneous frequency |
:$${\rm Min}\ [f_{\rm A}(t)] = f_{\rm T} - \Delta f_{\rm A} \hspace{0.15cm} \underline { = 899.932\,{\rm MHz}} \hspace{0.05cm}$$ | :$${\rm Min}\ [f_{\rm A}(t)] = f_{\rm T} - \Delta f_{\rm A} \hspace{0.15cm} \underline { = 899.932\,{\rm MHz}} \hspace{0.05cm}$$ | ||
| − | + | is obtained when all amplitude coefficients are negative. In this case $q_{\rm R}(t) = q_{\rm G}(t) = -1$. | |
| − | '''(2)''' | + | '''(2)''' The frequency at which the logarithmic power transfer function is $3 \ \rm dB$ less than $f = 0$ is called the 3dB cut-off frequency. |
| − | * | + | *This can also be expressed as follows: |
:$$\frac {|H(f = f_{\rm 3dB})|}{|H(f = 0)|}= \frac{1}{\sqrt{2}} \hspace{0.05cm}.$$ | :$$\frac {|H(f = f_{\rm 3dB})|}{|H(f = 0)|}= \frac{1}{\sqrt{2}} \hspace{0.05cm}.$$ | ||
| − | * | + | *In particular the Gauss low pass because of $H(f = 0) = 1$: |
:$$ H(f = f_{\rm 3dB})= {\rm e}^{-\pi\cdot ({f_{\rm 3dB}}/{2 f_{\rm G}})^2} = \frac{1}{\sqrt{2}}\hspace{0.3cm} | :$$ H(f = f_{\rm 3dB})= {\rm e}^{-\pi\cdot ({f_{\rm 3dB}}/{2 f_{\rm G}})^2} = \frac{1}{\sqrt{2}}\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}(\frac{f_{\rm 3dB}}{2 f_{\rm G}})^2 = \frac{{\rm ln}\hspace{0.1cm}\sqrt{2}}{\pi} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm G} = \sqrt{\frac{\pi}{4 \cdot {\rm ln}\hspace{0.1cm}\sqrt{2}}}\cdot f_{\rm 3dB}\hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm}(\frac{f_{\rm 3dB}}{2 f_{\rm G}})^2 = \frac{{\rm ln}\hspace{0.1cm}\sqrt{2}}{\pi} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm G} = \sqrt{\frac{\pi}{4 \cdot {\rm ln}\hspace{0.1cm}\sqrt{2}}}\cdot f_{\rm 3dB}\hspace{0.05cm}.$$ | ||
| − | * | + | *The numerical evaluation leads to $f_{\rm G} \approx 1.5 \cdot f_{\rm 3dB}$. |
| − | * | + | *{\f_{\rm 3dB} \cdot T = 0.3$ is followed by $f_{\rm G} \cdot T \underline{\approx 0.45}$. |
| − | |||
| Line 130: | Line 128: | ||
*Es ergeben sich also Impulsinterferenzen und man erhält: | *Es ergeben sich also Impulsinterferenzen und man erhält: | ||
:$${\rm Max} \hspace{0.12cm}[q_{\rm G}(t)] = g(t = 0) - 2 \cdot g(t = T) = 0.737 - 2 \cdot 0.131 \hspace{0.15cm} \underline {= 0.475 }\hspace{0.05cm}.$$ | :$${\rm Max} \hspace{0.12cm}[q_{\rm G}(t)] = g(t = 0) - 2 \cdot g(t = T) = 0.737 - 2 \cdot 0.131 \hspace{0.15cm} \underline {= 0.475 }\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | {{ML-Fuß}} | ||
| + | |||
| + | |||
| + | |||
| + | [[Category:Exercises for Mobile Communications|^3.3 Characteristics of GSM^]] | ||
| + | |||
| + | {{quiz-Header|Buchseite=Mobile Kommunikation/Die Charakteristika von GSM | ||
| + | }} | ||
| + | |||
| + | [[File:EN_Mob_A_3_5.png|right|frame|Verschiedene Signale bei GMSK-Modulation]] | ||
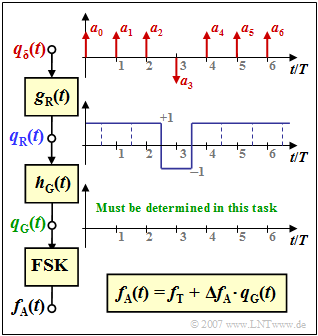
| + | The modulation method used for GSM is ''Gaussian Minimum Shift Keying'', short GMSK. This is a special type of FSK (''Frequency Shift Keying'') with CP-FSK (''Continuous Phase Matching''), where | ||
| + | *the modulation index has the smallest value that just satisfies the orthogonality condition: $h = 0.5$ ⇒ ''Minimum Shift Keying'', | ||
| + | *a Gaussian low pass with the impulse response $h_{\rm G}(t)$ is inserted before the FSK modulator, with the aim of saving even more bandwidth. | ||
| + | |||
| + | |||
| + | The graphic illustrates the situation: | ||
| + | |||
| + | *The digital message is represented by the amplitude coefficients $a_{\mu} ∈ \{±1\}$ which are applied to a Dirac pulse. It should be noted that the sequence drawn in is assumed for the subtask '''(3)'''. | ||
| + | |||
| + | *The symmetrical rectangular pulse with duration $T = T_{\rm B}$ (GSM bit duration) is dimensionless: | ||
| + | :$$g_{\rm R}(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |\hspace{0.05cm} t \hspace{0.05cm}| < T/2 \hspace{0.05cm}, \\ |\hspace{0.05cm} t \hspace{0.05cm}| > T/2 \hspace{0.05cm}. \\ \end{array}$$ | ||
| + | *This results for the rectangular signal | ||
| + | :$$q_{\rm R} (t) = q_{\rm \delta} (t) \star g_{\rm R}(t) = \sum_{\nu} a_{\nu}\cdot g_{\rm R}(t - \nu \cdot T)\hspace{0.05cm}.$$ | ||
| + | *The Gaussian low pass is given by its frequency response or impulse response: | ||
| + | :$$H_{\rm G}(f) = {\rm e}^{-\pi\cdot (\frac{f}{2 f_{\rm G}})^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\cdot (2 f_{\rm G}\cdot t)^2}\hspace{0.05cm},$$ | ||
| + | :where the system theoretical cut-off frequency $f_{\rm G}$ is used. In the GSM specification, however, the 3dB cut-off frequency is specified with $f_{\rm 3dB} = 0.3/T$ . From this, $f_{\rm G}$ can be calculated directly - see subtask '''(2)'''. | ||
| + | |||
| + | *The signal after the gauss low pass is thus | ||
| + | :$$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$ | ||
| + | Here $g(t)$ is referred to as ''frequency pulse''. For this one: | ||
| + | :$$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$ | ||
| + | |||
| + | *With the low pass filtered signal $q_{\rm G}(t)$, the carrier frequency $f_{\rm T}$ and the frequency deviation $\Delta f_{\rm A}$ can thus be written for the instantaneous frequency at the output of the FSK modulator::$$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Notes:'' | ||
| + | |||
| + | *This exercise belongs to the chapter [[Mobile_Kommunikation/Die_Charakteristika_von_GSM|Die Charakteristika von GSM]]. | ||
| + | *Reference is also made to the chapter [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle|Funkschnittstelle]] in the book „Beispiele von Nachrichtensystemen”. | ||
| + | |||
| + | *For your calculations use the exemplary values $f_{\rm T} = 900 \ \ \rm MHz$ and $\Delta f_{\rm A} = 68 \ \rm kHz$. | ||
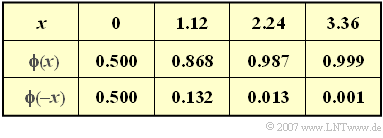
| + | *Use the Gaussian integral to solve the task (some numerical values are given in the table) | ||
| + | [[File:P_ID2226__Bei_A_3_4b.png|right|frame|some values of the Gaussian integral]] | ||
| + | :$$\phi(x) =\frac {1}{\sqrt{2 \pi}} \cdot \int^{x} _{-\infty} {\rm e}^{-u^2/2}\,{\rm d}u \hspace{0.05cm}.$$ | ||
| + | <br clear=all> | ||
| + | |||
| + | |||
| + | |||
| + | ===Fragebogen=== | ||
| + | |||
| + | <quiz display=simple> | ||
| + | |||
| + | {In what range of values can the instantaneous frequency $f_{\rm A}(t)$ fluctuate? Which requirements must be met? | ||
| + | |type="{}"} | ||
| + | ${\rm Max} \ \big[f_{\rm A}(t)\big] \ = \hspace{0.2cm} $ { 900.068 0.01% } $\ \rm MHz$ | ||
| + | ${\rm Min} \ \big[f_{\rm A}(t)\big] \ = \hspace{0.28cm} $ { 899.932 0.01% } $\ \rm MHz$ | ||
| + | |||
| + | {Which (normalized) system-theoretical cut-off frequency of the Gaussian low pass results from the requirement $f_{\rm 3dB} \cdot T = 0.3$? | ||
| + | |type="{}"} | ||
| + | $f_{\rm G} \cdot T \ = \ $ { 0.45 3% } | ||
| + | |||
| + | {Calculate the frequency pulse $g(t)$ using the function $\phi (x)$. How large is the pulse value $g(t = 0)$? | ||
| + | |type="{}"} | ||
| + | $g(t = 0) \ = \ $ { 0.737 3% } | ||
| + | |||
| + | {Which signal value results for $q_{\rm G}(t = 3T)$ with $a_{3} = -1$ and $a_{\mu \ne 3} = +1$? What is the instantaneous frequency $f_{\rm A}(t = 3T)$? | ||
| + | |type="{}"} | ||
| + | $q_{\rm G}(t = 3T) \ = \ $ { -0.51822--0.42978 } | ||
| + | |||
| + | {Calculate the pulse values $g(t = ±T)$ of the frequency pulse | ||
| + | |type="{}"} | ||
| + | $g(t = ±T) \ = \ $ { 0.131 3% } | ||
| + | |||
| + | {The amplitude coefficients are alternating. What is the maximum amount of $q_{G}(t)$ ? Consider $g(t ≥ 2 T) \approx 0$. | ||
| + | |type="{}"} | ||
| + | ${\rm Max} \ |q_{\rm G}(t)| \ = \ $ { 0.475 3% } | ||
| + | |||
| + | |||
| + | |||
| + | </quiz> | ||
| + | |||
| + | ===Sample solution=== | ||
| + | {{ML-Kopf}} | ||
| + | |||
| + | '''(1)''' If all amplitude coefficients $a_{\mu}$ are equal to $+1$, then $q_{\rm R}(t) = 1$ is a constant. Thus, the Gaussian low pass has no influence and $q_{\rm G}(t) = 1$ results. | ||
| + | *The maximum frequency is thus | ||
| + | :$${\rm Max}\ [f_{\rm A}(t)] = f_{\rm T} + \Delta f_{\rm A} \hspace{0.15cm} \underline {= 900.068\,{\rm MHz}} \hspace{0.05cm}.$$ | ||
| + | *The minimum instantaneous frequency | ||
| + | :$${\rm Min}\ [f_{\rm A}(t)] = f_{\rm T} - \Delta f_{\rm A} \hspace{0.15cm} \underline { = 899.932\,{\rm MHz}} \hspace{0.05cm}$$ | ||
| + | is obtained when all amplitude coefficients are negative. In this case $q_{\rm R}(t) = q_{\rm G}(t) = -1$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' The frequency at which the logarithmic power transfer function is $3 \ \rm dB$ less than $f = 0$ is called the 3dB cut-off frequency. | ||
| + | *This can also be expressed as follows: | ||
| + | :$$\frac {|H(f = f_{\rm 3dB})|}{|H(f = 0)|}= \frac{1}{\sqrt{2}} \hspace{0.05cm}.$$ | ||
| + | *In particular the Gauss low pass because of $H(f = 0) = 1$: | ||
| + | :$$ H(f = f_{\rm 3dB})= {\rm e}^{-\pi\cdot ({f_{\rm 3dB}}/{2 f_{\rm G}})^2} = \frac{1}{\sqrt{2}}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}(\frac{f_{\rm 3dB}}{2 f_{\rm G}})^2 = \frac{{\rm ln}\hspace{0.1cm}\sqrt{2}}{\pi} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm G} = \sqrt{\frac{\pi}{4 \cdot {\rm ln}\hspace{0.1cm}\sqrt{2}}}\cdot f_{\rm 3dB}\hspace{0.05cm}.$$ | ||
| + | *The numerical evaluation leads to $f_{\rm G} \approx 1.5 \cdot f_{\rm 3dB}$. | ||
| + | |||
| + | |||
Revision as of 08:47, 30 June 2020
The modulation method used for GSM is Gaussian Minimum Shift Keying, short GMSK. This is a special type of FSK (Frequency Shift Keying) with CP-FSK (Continuous Phase Matching), where
- the modulation index has the smallest value that just satisfies the orthogonality condition: $h = 0.5$ ⇒ Minimum Shift Keying,
- a Gaussian low pass with the impulse response $h_{\rm G}(t)$ is inserted before the FSK modulator, with the aim of saving even more bandwidth.
The graphic illustrates the situation:
- The digital message is represented by the amplitude coefficients $a_{\mu} ∈ \{±1\}$ which are applied to a Dirac pulse. It should be noted that the sequence drawn in is assumed for the subtask (3).
- The symmetrical rectangular pulse with duration $T = T_{\rm B}$ (GSM bit duration) is dimensionless:
- $$g_{\rm R}(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |\hspace{0.05cm} t \hspace{0.05cm}| < T/2 \hspace{0.05cm}, \\ |\hspace{0.05cm} t \hspace{0.05cm}| > T/2 \hspace{0.05cm}. \\ \end{array}$$
- This results for the rectangular signal
- $$q_{\rm R} (t) = q_{\rm \delta} (t) \star g_{\rm R}(t) = \sum_{\nu} a_{\nu}\cdot g_{\rm R}(t - \nu \cdot T)\hspace{0.05cm}.$$
- The Gaussian low pass is given by its frequency response or impulse response:
- $$H_{\rm G}(f) = {\rm e}^{-\pi\cdot (\frac{f}{2 f_{\rm G}})^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\cdot (2 f_{\rm G}\cdot t)^2}\hspace{0.05cm},$$
- where the system theoretical cut-off frequency $f_{\rm G}$ is used. In the GSM specification, however, the 3dB cut-off frequency is specified with $f_{\rm 3dB} = 0.3/T$ . From this, $f_{\rm G}$ can be calculated directly - see subtask (2).
- The signal after the gauss low pass is thus
- $$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$
Here $g(t)$ is referred to as frequency pulse. For this one:
- $$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$
- With the low pass filtered signal $q_{\rm G}(t)$, the carrier frequency $f_{\rm T}$ and the frequency deviation $\Delta f_{\rm A}$ can thus be written for the instantaneous frequency at the output of the FSK modulator::$$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$
Notes:
- This exercise belongs to the chapter Die Charakteristika von GSM.
- Reference is also made to the chapter Funkschnittstelle in the book „Beispiele von Nachrichtensystemen”.
- For your calculations use the exemplary values $f_{\rm T} = 900 \ \ \rm MHz$ and $\Delta f_{\rm A} = 68 \ \rm kHz$.
- Use the Gaussian integral to solve the task (some numerical values are given in the table)
- $$\phi(x) =\frac {1}{\sqrt{2 \pi}} \cdot \int^{x} _{-\infty} {\rm e}^{-u^2/2}\,{\rm d}u \hspace{0.05cm}.$$
Fragebogen
Sample solution
(1) If all amplitude coefficients $a_{\mu}$ are equal to $+1$, then $q_{\rm R}(t) = 1$ is a constant. Thus, the Gaussian low pass has no influence and $q_{\rm G}(t) = 1$ results.
- The maximum frequency is thus
- $${\rm Max}\ [f_{\rm A}(t)] = f_{\rm T} + \Delta f_{\rm A} \hspace{0.15cm} \underline {= 900.068\,{\rm MHz}} \hspace{0.05cm}.$$
- The minimum instantaneous frequency
- $${\rm Min}\ [f_{\rm A}(t)] = f_{\rm T} - \Delta f_{\rm A} \hspace{0.15cm} \underline { = 899.932\,{\rm MHz}} \hspace{0.05cm}$$
is obtained when all amplitude coefficients are negative. In this case $q_{\rm R}(t) = q_{\rm G}(t) = -1$.
(2) The frequency at which the logarithmic power transfer function is $3 \ \rm dB$ less than $f = 0$ is called the 3dB cut-off frequency.
- This can also be expressed as follows:
- $$\frac {|H(f = f_{\rm 3dB})|}{|H(f = 0)|}= \frac{1}{\sqrt{2}} \hspace{0.05cm}.$$
- In particular the Gauss low pass because of $H(f = 0) = 1$:
- $$ H(f = f_{\rm 3dB})= {\rm e}^{-\pi\cdot ({f_{\rm 3dB}}/{2 f_{\rm G}})^2} = \frac{1}{\sqrt{2}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}(\frac{f_{\rm 3dB}}{2 f_{\rm G}})^2 = \frac{{\rm ln}\hspace{0.1cm}\sqrt{2}}{\pi} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm G} = \sqrt{\frac{\pi}{4 \cdot {\rm ln}\hspace{0.1cm}\sqrt{2}}}\cdot f_{\rm 3dB}\hspace{0.05cm}.$$
- The numerical evaluation leads to $f_{\rm G} \approx 1.5 \cdot f_{\rm 3dB}$.
- {\f_{\rm 3dB} \cdot T = 0.3$ is followed by $f_{\rm G} \cdot T \underline{\approx 0.45}$. '''(3)''' Der gesuchte Frequenzimpuls ${\rm g}(t)$ ergibt sich aus der Faltung von Rechteckfunktion $g_{\rm R}(t)$ mit der Impulsantwort $h_{\rm G}(t)$: :'"`UNIQ-MathJax54-QINU`"' *Mit der Substitution $u^{2} = 8π \cdot {f_{G}}^{2} \cdot \tau^{2}$ und der Funktion $\phi (x)$ kann man hierfür auch schreiben: :'"`UNIQ-MathJax55-QINU`"' *Für die Zeit $t = 0$ gilt unter Berücksichtigung von $\phi (-x) = 1 - \phi (x)$ und $f_{\rm G} \cdot T = 0.45$: :'"`UNIQ-MathJax56-QINU`"' '''(4)''' Mit $a_{3} = +1$ würde sich $q_{\rm G}(t = 3 T) = 1$ ergeben. Aufgrund der Linearität gilt somit: :'"`UNIQ-MathJax57-QINU`"' '''(5)''' Mit dem Ergebnis aus (3) und $f_{\rm G} \cdot T = 0.45$ erhält man: :'"`UNIQ-MathJax58-QINU`"' *Der Impulswert $g(t = -T)$ ist aufgrund der Symmetrie des Gaußtiefpasses genau so groß. '''(6)''' Bei alternierender Folge sind aus Symmetriegründen die Beträge $|q_{\rm G}(\mu \cdot T)|$ bei allen Vielfachen der Bitdauer $T$ alle gleich. *Alle Zwischenwerte bei $t \approx \mu \cdot T$ sind dagegen kleiner. *Unter Berücksichtigung von $g(t ≥ 2T) \approx 0$ wird jeder einzelne Impulswert $g(0)$ durch den vorangegangenen Impuls mit $g(t = T)$ verkleinert, ebenso vom folgenden Impuls mit $g(t = -T)$. *Es ergeben sich also Impulsinterferenzen und man erhält: :'"`UNIQ-MathJax59-QINU`"' '"`UNIQ--html-00000004-QINU`"' [[Category:Exercises for Mobile Communications|^3.3 Characteristics of GSM^]] '"`UNIQ--html-00000005-QINU`"' [[Mobile Kommunikation/Die Charakteristika von GSM | Return to book]] '"`UNIQ--html-00000006-QINU`"' [[File:EN_Mob_A_3_5.png|right|frame|Verschiedene Signale bei GMSK-Modulation]] The modulation method used for GSM is ''Gaussian Minimum Shift Keying'', short GMSK. This is a special type of FSK (''Frequency Shift Keying'') with CP-FSK (''Continuous Phase Matching''), where *the modulation index has the smallest value that just satisfies the orthogonality condition: $h = 0.5$ ⇒ ''Minimum Shift Keying'', *a Gaussian low pass with the impulse response $h_{\rm G}(t)$ is inserted before the FSK modulator, with the aim of saving even more bandwidth. The graphic illustrates the situation: *The digital message is represented by the amplitude coefficients $a_{\mu} ∈ \{±1\}$ which are applied to a Dirac pulse. It should be noted that the sequence drawn in is assumed for the subtask '''(3)'''. *The symmetrical rectangular pulse with duration $T = T_{\rm B}$ (GSM bit duration) is dimensionless: :'"`UNIQ-MathJax60-QINU`"' *This results for the rectangular signal :'"`UNIQ-MathJax61-QINU`"' *The Gaussian low pass is given by its frequency response or impulse response: :'"`UNIQ-MathJax62-QINU`"' :where the system theoretical cut-off frequency $f_{\rm G}$ is used. In the GSM specification, however, the 3dB cut-off frequency is specified with $f_{\rm 3dB} = 0.3/T$ . From this, $f_{\rm G}$ can be calculated directly - see subtask '''(2)'''. *The signal after the gauss low pass is thus :'"`UNIQ-MathJax63-QINU`"' Here $g(t)$ is referred to as ''frequency pulse''. For this one: :'"`UNIQ-MathJax64-QINU`"' *With the low pass filtered signal $q_{\rm G}(t)$, the carrier frequency $f_{\rm T}$ and the frequency deviation $\Delta f_{\rm A}$ can thus be written for the instantaneous frequency at the output of the FSK modulator::'"`UNIQ-MathJax65-QINU`"' ''Notes:'' *This exercise belongs to the chapter [[Mobile_Kommunikation/Die_Charakteristika_von_GSM|Die Charakteristika von GSM]]. *Reference is also made to the chapter [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle|Funkschnittstelle]] in the book „Beispiele von Nachrichtensystemen”. *For your calculations use the exemplary values $f_{\rm T} = 900 \ \ \rm MHz$ and $\Delta f_{\rm A} = 68 \ \rm kHz$. *Use the Gaussian integral to solve the task (some numerical values are given in the table) [[File:P_ID2226__Bei_A_3_4b.png|right|frame|some values of the Gaussian integral]] :'"`UNIQ-MathJax66-QINU`"' <br clear="all"> ==='"`UNIQ--h-2--QINU`"'Fragebogen=== '"`UNIQ--quiz-00000007-QINU`"' ==='"`UNIQ--h-3--QINU`"'Sample solution=== '"`UNIQ--html-00000003-QINU`"' '''(1)''' If all amplitude coefficients $a_{\mu}$ are equal to $+1$, then $q_{\rm R}(t) = 1$ is a constant. Thus, the Gaussian low pass has no influence and $q_{\rm G}(t) = 1$ results. *The maximum frequency is thus :'"`UNIQ-MathJax67-QINU`"' *The minimum instantaneous frequency :'"`UNIQ-MathJax68-QINU`"' is obtained when all amplitude coefficients are negative. In this case $q_{\rm R}(t) = q_{\rm G}(t) = -1$. '''(2)''' The frequency at which the logarithmic power transfer function is $3 \ \rm dB$ less than $f = 0$ is called the 3dB cut-off frequency. *This can also be expressed as follows: :'"`UNIQ-MathJax69-QINU`"' *In particular the Gauss low pass because of $H(f = 0) = 1$: :'"`UNIQ-MathJax70-QINU`"' *The numerical evaluation leads to $f_{\rm G} \approx 1.5 \cdot f_{\rm 3dB}$.