Difference between revisions of "Signal Representation/Signal classification"
m (Oezdemir moved page Signal Representation/Klassifizierung von Signalen to Signal Representation/Signal classification) |
|||
| Line 5: | Line 5: | ||
}} | }} | ||
| − | ==Deterministic and | + | ==Deterministic and Stochastic Signals== |
<br> | <br> | ||
In every communication system both deterministic and stochastic signals occur. | In every communication system both deterministic and stochastic signals occur. | ||
| Line 41: | Line 41: | ||
| − | == | + | ==Causal and Non-Causal Signals== |
<br> | <br> | ||
| − | In | + | In communications engineering one often reckons with temporally unlimited signals; the definition range of the signal then extends from $t = -\infty$ to $t=+\infty$. |
| − | In | + | In reality, however, there are no such signals, because every signal had to be switched on at some point. If one chooses - arbitrarily, but nevertheless meaningfully - the switch-on time $t = 0$, then one comes to the following classification: |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | A signal $x(t)$ is called '''causal''', if it does not exist for all times $t < 0$ or is identical zero. If this condition is not fulfilled, a ‘’non-causal'' signal (or system) exists.}} | |
| − | In | + | In this book „Signal representation” mostly causal signals and systems are considered. This has the following reasons: |
| − | * | + | *Non-causal signals (and systems) are mathematically easier to handle than causal ones. For example, the spectral function can be determined here by means of Fourier transformations and one does not need extensive knowledge of function theory as in the Laplace transformation. |
| − | * | + | *Non-causal signals and systems describe the situation completely and correctly, if one ignores the problem of the switch-on process and is therefore only interested in the ''steady state'' . |
| − | + | The description of causal signals and systems using the [[Linear_and_Time_Invariant_Systems/Laplace–Transformation_und_p–Übertragungsfunktion|Laplace Transform]] is shown in the book [[Lineare_zeitinvariante_Systeme|Linear Time-Invariant Systems]]. | |
| − | [[File:EN_Sig_T_1_2_S2.png|right|frame| | + | [[File:EN_Sig_T_1_2_S2.png|right|frame|Causal and non-causal system]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ |
| − | + | You can see a causal transmission system in the upper graphic: | |
| − | * | + | *If a unit step function $x(t)$ is applied to its input, then the output signal $y(t)$ can only increase from zero to its maximum value after time $t = 0$ . |
| − | * | + | *Otherwise the causal connection that the effect cannot begin before the cause would not be fulfilled. |
| − | + | The causality In the lower pictureis no longer given. As you can easily see in this example, an additional runtime of one millisecond is enough to change from the non-causal to the causal representation.}} | |
| − | == | + | ==Energy Limited and Power Limited Signals== |
<br> | <br> | ||
| − | + | At this place first two important signal description quantities must be introduced, namely the '''energy''' and the '''power'''. | |
| − | * | + | *In terms of physics, energy corresponds to work and has, for example, the unit "Ws". |
| − | * | + | *The power is defined as "work per time" and therefore has the unit "W". |
| − | + | According to the elementary laws of electrical engineering, both values are dependent on the resistance $R$ . In order to eliminate this dependency, the resistance $R=1 \,\Omega$ is often used as a basis in communications engineering. Then the following definitions apply: | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The '''energy''' of the signal $x(t)$ is to calculate as follows: | |
:$$E_x=\lim_{T_{\rm M}\to\infty} \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$}} | :$$E_x=\lim_{T_{\rm M}\to\infty} \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$}} | ||
| Line 92: | Line 92: | ||
:$$P_x = \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M} } \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$ | :$$P_x = \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M} } \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$ | ||
| − | + | Where $T_{\rm M}$ is the assumed measurement duration during which the signal is observed, symmetrically with respect to the time origin $(t = 0)$ . In general, this time interval must be chosen very large; ideally $T_{\rm M}$ should be towards infinity.}} | |
| − | + | If $x(t)$ denotes a stress curve with the unit $\text{V}$, according to the above equations is for | |
| − | * | + | *the signal energy the unit $\text{V}^2\text{s}$, |
| − | * | + | *the signal power the unit $\text{V}^2$. |
| − | + | This statement also means: In the above definitions the reference resistance $R=1\,\Omega$ is already implicit. | |
Revision as of 16:26, 31 August 2020
Contents
Deterministic and Stochastic Signals
In every communication system both deterministic and stochastic signals occur.
$\text{Definition:}$ A deterministic signal exists, if its time functions $x(t)$ can be described completely in analytical form.
Since the time function $x(t)$ for all times $t$ is known and can be specified unambiguously, a spectral function $X(f)$ which can be calculated using the Fourier series or Fourier transform .
$\text{Definition:}$ One refers to a 'stochastic signal or to a random signal, if the signal course $x(t)$ is not - or at least not completely – describable in mathematical form. Such a signal cannot be predicted exactly for the future.
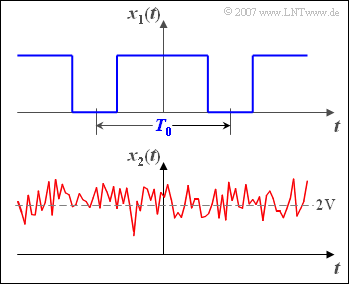
$\text{Example 1:}$ The graph shows time histories of a deterministic and a stochastic signal:
- At the top a periodic square wave signal $x_1(t)$ with period duration $T_0$ ⇒ deterministic signal,
- below a Gaussian noise signal $x_2(t)$ with the mean value $2\ \rm V $ ⇒ stochastic signal.
For such a non-deterministic signal $x_2(t)$ no spectral function $X_2(f)$ can be specified, since Fourier series/Fourier transform requires the exact knowledge of the time function for all times $t$
Information-carrying signals are always of stochastic nature. Their description as well as the definition of suitable parameters is given in the book Theory of Stochastic Signals.
However, the deterministic signals are also of great importance for communications engineering. Examples of this are:
- test signals for the design of communication systems,
- carrier signals for frequency multiplex systems, and
- a pulse for sampling an analog signal or for time regeneration of a digital signal.
Causal and Non-Causal Signals
In communications engineering one often reckons with temporally unlimited signals; the definition range of the signal then extends from $t = -\infty$ to $t=+\infty$.
In reality, however, there are no such signals, because every signal had to be switched on at some point. If one chooses - arbitrarily, but nevertheless meaningfully - the switch-on time $t = 0$, then one comes to the following classification:
$\text{Definition:}$ A signal $x(t)$ is called causal, if it does not exist for all times $t < 0$ or is identical zero. If this condition is not fulfilled, a ‘’non-causal signal (or system) exists.
In this book „Signal representation” mostly causal signals and systems are considered. This has the following reasons:
- Non-causal signals (and systems) are mathematically easier to handle than causal ones. For example, the spectral function can be determined here by means of Fourier transformations and one does not need extensive knowledge of function theory as in the Laplace transformation.
- Non-causal signals and systems describe the situation completely and correctly, if one ignores the problem of the switch-on process and is therefore only interested in the steady state .
The description of causal signals and systems using the Laplace Transform is shown in the book Linear Time-Invariant Systems.
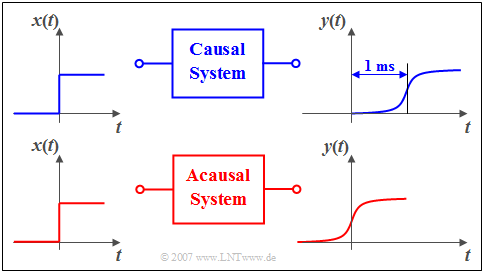
$\text{Example 2:}$ You can see a causal transmission system in the upper graphic:
- If a unit step function $x(t)$ is applied to its input, then the output signal $y(t)$ can only increase from zero to its maximum value after time $t = 0$ .
- Otherwise the causal connection that the effect cannot begin before the cause would not be fulfilled.
The causality In the lower pictureis no longer given. As you can easily see in this example, an additional runtime of one millisecond is enough to change from the non-causal to the causal representation.
Energy Limited and Power Limited Signals
At this place first two important signal description quantities must be introduced, namely the energy and the power.
- In terms of physics, energy corresponds to work and has, for example, the unit "Ws".
- The power is defined as "work per time" and therefore has the unit "W".
According to the elementary laws of electrical engineering, both values are dependent on the resistance $R$ . In order to eliminate this dependency, the resistance $R=1 \,\Omega$ is often used as a basis in communications engineering. Then the following definitions apply:
$\text{Definition:}$ The energy of the signal $x(t)$ is to calculate as follows:
- $$E_x=\lim_{T_{\rm M}\to\infty} \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$
$\text{Definition:}$ Zur Berechnung der (mittleren) Leistung muss vor dem Grenzübergang noch durch die Zeit $T_{\rm M}$ dividiert werden:
- $$P_x = \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M} } \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} x^2(t)\,{\rm d}t.$$
Where $T_{\rm M}$ is the assumed measurement duration during which the signal is observed, symmetrically with respect to the time origin $(t = 0)$ . In general, this time interval must be chosen very large; ideally $T_{\rm M}$ should be towards infinity.
If $x(t)$ denotes a stress curve with the unit $\text{V}$, according to the above equations is for
- the signal energy the unit $\text{V}^2\text{s}$,
- the signal power the unit $\text{V}^2$.
This statement also means: In the above definitions the reference resistance $R=1\,\Omega$ is already implicit.
$\text{Beispiel 3:}$ Nun werden Energie und Leistung zweier beispielhafter Signale berechnet.
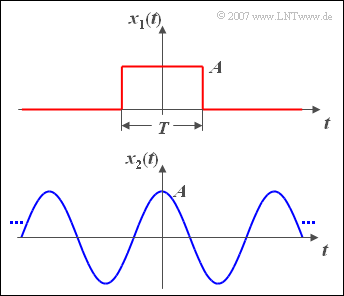
Die obere Grafik zeigt einen Rechteckimpuls $x_1(t)$ mit Amplitude $A$ und Dauer $T$.
- Die Signalenergie dieses Impulses ist $E_1 = A^2 \cdot T$.
- Für die Signalleistung ergibt sich aufgrund der Division durch $T_{\rm M}$ und Grenzwertbildung $(T_{\rm M} \to \infty)$ der Wert $P_1 = 0$.
Beim Cosinussignal $x_2(t)$ mit der Amplitude $A$ entsprechend der unteren Skizze gilt:
- Die Signalleistung ist unabhängig von der Frequenz gleich $P_2 = A^2/2$.
- Die Signalenergie $E_2$ (Integral über die Leistung für alle Zeiten) ist unendlich.
Mit $A = 4 \ {\rm V}$ ergibt sich für die Leistung $P_2 = 8 \ {\rm V}^2$. Mit dem Widerstand von $R = 50 \,\,\Omega$ entspricht dies der physikalischen Leistung ${8}/{50} \,\,{\rm V}\hspace{-0.1cm}/{\Omega}= 160\,\, {\rm mW}$.
Entsprechend diesem Beispiel gibt es die folgenden Klassifizierungsmerkmale:
$\text{Definition:}$ Ein Signal $x(t)$ mit endlicher Energie $E_x$ und unendlich kleiner Leistung $(P_x = 0)$ bezeichnet man als energiebegrenzt.
- Impulsförmige Signale wie das Signal $x_1(t)$ im obigen Beispiel sind stets energiebegrenzt. Meist sind hier die Signalwerte nur für eine endliche Zeitdauer von Null verschieden. In anderen Worten: Solche Signale sind oft auch zeitbegrenzt.
- Aber auch zeitlich unbegrenzte Signale können durchaus eine endliche Energie besitzen. In späteren Kapiteln finden Sie weitere Informationen zu energiebegrenzten und damit aperiodischen Signalen, zu denen beispielsweise der Gaußimpuls und der Exponentialimpuls gehören.
$\text{Definition:}$ Ein Signal $x(t)$ mit endlicher Leistung $P_x$ und dementsprechend unendlich großer Energie $(E_x \to \infty)$ bezeichnet man als leistungsbegrenzt.
- Alle leistungsbegrenzten Signale sind auch zeitlich unendlich weit ausgedehnt.
- Beispiele hierfür sind das Gleichsignal und Harmonische Schwingungen wie das Cosinussignal $x_2(t)$ im $\text{Beispiel 3}$, die im Kapitel Periodische Signale ausführlich beschrieben werden.
- Auch die meisten stochastischen Signale sind leistungsbegrenzt – siehe Buch Stochastische Signaltheorie.
Wertkontinuierliche und wertdiskrete Signale
$\text{Definition:}$ Ein Signal bezeichnet man als wertkontinuierlich, wenn der entscheidende Signalparameter – zum Beispiel der Augenblickswert – alle Werte eines Kontinuums (beispielsweise eines Intervalls) annehmen kann. Sind für den Signalparameter dagegen nur abzählbar viele verschiedene Werte möglich, so ist das Signal wertdiskret. Die Anzahl der möglichen Werte bezeichnet man als die Stufenzahl $M$ oder als den Werteumfang.
- Bei den analogen Übertragungssystemen wird stets mit wertkontinuierlichen Signalen gearbeitet.
- Bei Digitalsystemen sind dagegen die meisten Signale – aber nicht alle – wertdiskret.
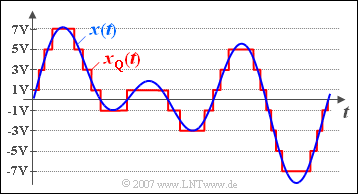
$\text{Beispiel 4:}$ Das obere Bild zeigt in blau einen Ausschnitt eines wertkontinuierlichen Signals $x(t)$, das Werte zwischen $\pm 8\ \rm V$ annehmen kann.
- In roter Farbe erkennt man das auf $M = 8$ Quantisierungsstufen diskretisierte Signal $x_{\rm Q}(t)$ mit den möglichen Signalwerten $\pm 1\ \rm V$, $\pm 3\ \rm V$, $\pm 5\ \rm V$ und $\pm 7\ \rm V$.
- Bei diesem Signal $x_{\rm Q}(t)$ wurde der Augenblickswert als der entscheidende Signalparameter betrachtet.
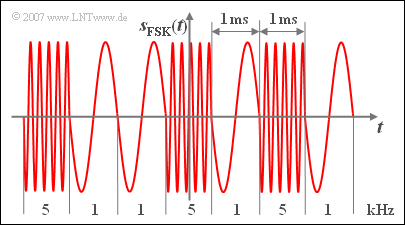
Bei einem FSK-System (Frequency Shift Keying) ist dagegen die Augenblicksfrequenz der wesentliche Signalparameter.
Deshalb bezeichnet man auch das unten dargestellte Signal $s_{\rm FSK}(t)$ als wertdiskret mit der Stufenzahl $M = 2$ und den möglichen Frequenzen $1 \ \rm kHz$ und $5 \ \rm kHz$, obwohl der Augenblickswert wertkontinuierlich ist.
Zeitkontinuierliche und zeitdiskrete Signale
Bei den bisher betrachteten Signalen war der Signalparameter zu jedem beliebigen Zeitpunkt definiert. Man spricht dann von einem zeitkontinuierlichen Signal.
$\text{Definition:}$ Bei einem zeitdiskreten Signal ist im Gegensatz dazu der Signalparameter nur zu den diskreten Zeitpunkten $t_\nu$ definiert, wobei man diese Zeitpunkte meist äquidistant wählt: $t_\nu = \nu \cdot T_{\rm A}$.
Da ein solches Signal beispielsweise durch Abtastung eines zeitkontinuierlichen Signals entsteht, bezeichnen wir $T_{\rm A}$ als den Abtastzeitabstand und dessen Kehrwert $f_{\rm A} = 1/T_{\rm A}$ als die Abtastfrequenz.
Weiter gilt:
- Ein zeitdiskretes Signal $x(t)$ ist durch die zeitliche Folge $\left \langle x_\nu \right \rangle$ seiner Abtastwerte vollständig bestimmt.
- Diese Abtastwerte können dabei sowohl wertkontinuierlich als auch wertdiskret sein.
- Die mathematische Beschreibung zeitdiskreter Signale erfolgt im Kapitel Zeitdiskrete Signaldarstellung.
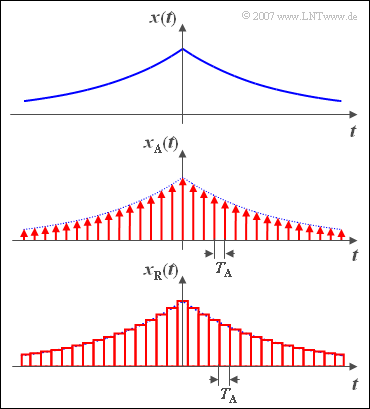
$\text{Beispiel 5:}$ Das zeitdiskrete Signal $x_{\rm A}(t)$ erhält man nach Abtastung des oben dargestellten zeit- und wertkontinuierlichen Nachrichtensignals $x(t)$ im Abstand $T_{\rm A}$.
- Der unten skizzierte Zeitverlauf $x_{\rm R}(t)$ unterscheidet sich von der echten zeitdiskreten Darstellung $x_{\rm A}(t)$ dadurch, dass die unendlich schmalen Abtastwerte (mathematisch mit Diracimpulsen beschreibbar) durch Rechteckimpulse der Dauer $T_{\rm A}$ ersetzt sind.
- Ein solches Signal kann nach obiger Definition ebenfalls als zeitdiskret bezeichnet werden.
Analogsignale und Digitalsignale
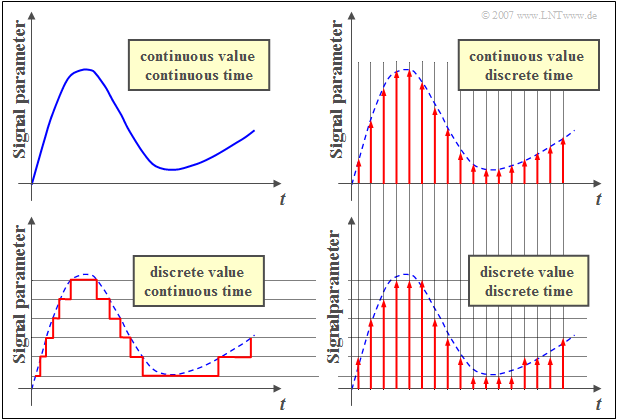
$\text{Beispiel 6:}$ In der Grafik sind an einem Beispiel die folgenden Signaleigenschaften verdeutlicht:
- „wertkontinuierlich” und „wertdiskret”, sowie
- „zeitkontinuierlich” und „zeitdiskret”.
Daneben gelten noch folgende Festlegungen:
$\text{Definition:}$ Ist ein Signal sowohl wert– als auch zeitkontinuierlich, so spricht man auch von einem Analogsignal. Solche Signale bilden einen kontinuierlichen Vorgang kontinuierlich ab. Beispiele hierfür sind Sprach–, Musik–, Bild– und Mess Signale.
$\text{Definition:}$ Ein Digitalsignal ist dagegen stets wert– und zeitdiskret und die darin enthaltene Nachricht besteht aus den Symbolen eines Symbolvorrats. Es kann beispielsweise ein abgetastetes und quantisiertes (sowie in irgendeiner Form codiertes) Sprach–, Musik– oder Bildsignal sein, aber auch ein Datensignal, wenn im Internet eine Datei von einem Server heruntergeladen wird.
Je nach Stufenzahl sind Digitalsignale auch noch unter anderen Namen bekannt, beispielsweise
- mit $M = 2$: binäres Digitalsignal oder Binärsignal,
- mit $M = 3$: ternäres Digitalsignal oder Ternärsignal,
- mit $M = 4$: quaternäres Digitalsignal oder Quaternärsignal.
Das Lernvideo Analoge und digitale Signale fasst die in diesem Kapitel behandelten Klassifizierungsmerkmale in kompakter Weise zusammen.
Aufgaben zum Kapitel
Aufgabe 1.2: Signalklassifizierung
Aufgabe 1.2Z: Pulscodemodulation